Элементы математического анализа
Пределы и непрерывность
Отметим некоторые теоремы о пределах, которые часто применяются для решения задач.
Если существуют конечные пределы 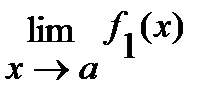 и
и 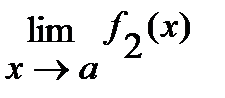 , то
, то
1) 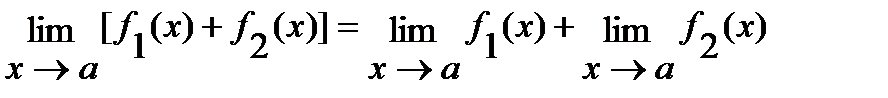 ;
;
2) 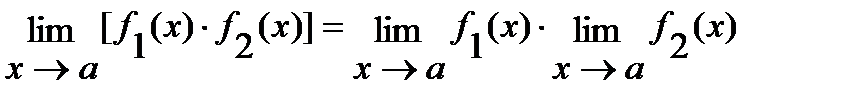 ;
;
3) 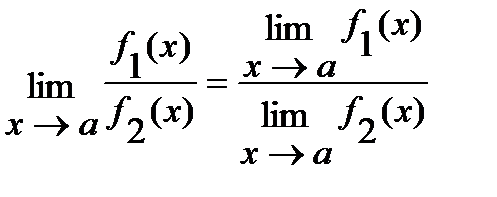 ( если
( если 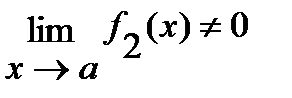 ).
).
Отметим еще два замечательных предела и следствия из них:
1) 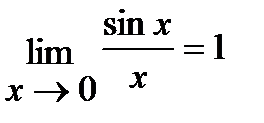 ;
;
2) 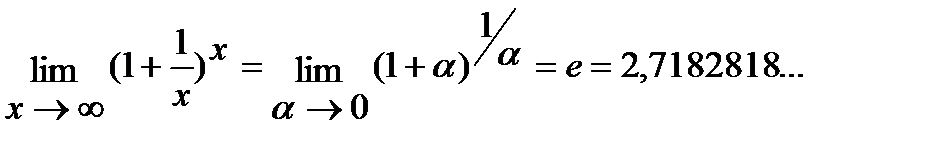 ;
;
3) 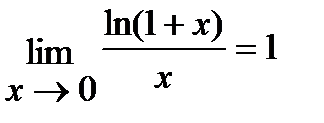 ; 4)
; 4) 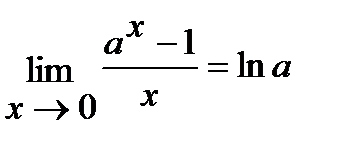 ; 5)
; 5) 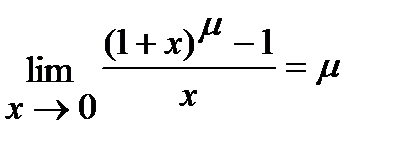 .
.
Задача. Найти указанные пределы, не пользуясь правилом Лопиталя:
а) 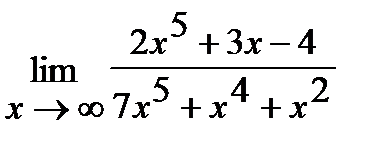 ;
;
б) 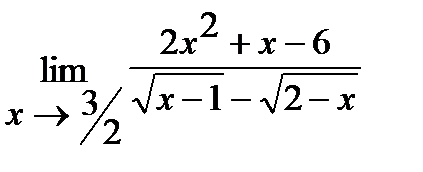 ;
;
в) 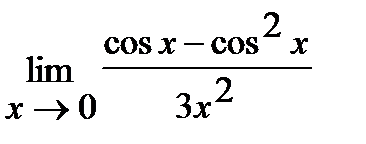 ;
;
г) 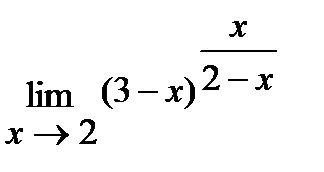 ;
;
д) 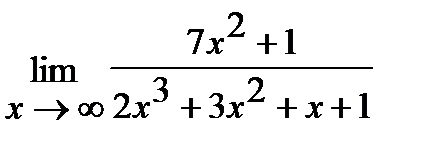 ;
;
е) 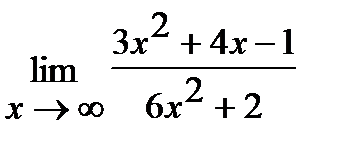 . ж)
. ж) 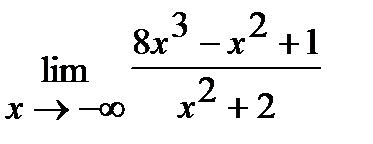 .
.
Решение. а) Если 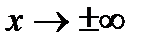 , то для нахождения предела частного двух многочленов достаточно разделить и числитель, и знаменатель дроби, стоящей под знаком предела, на
, то для нахождения предела частного двух многочленов достаточно разделить и числитель, и знаменатель дроби, стоящей под знаком предела, на 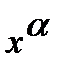 , где
, где 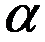 - степень многочлена, стоящего в знаменателе:
- степень многочлена, стоящего в знаменателе: 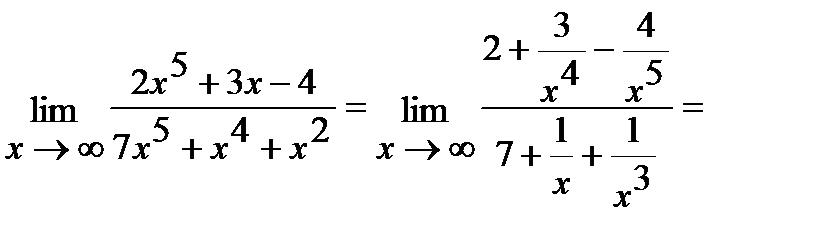
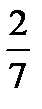 .
.
б) Умножим числитель и знаменатель дроби на 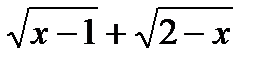 , избавившись тем самым от иррациональности в знаменателе. Итак,
, избавившись тем самым от иррациональности в знаменателе. Итак,
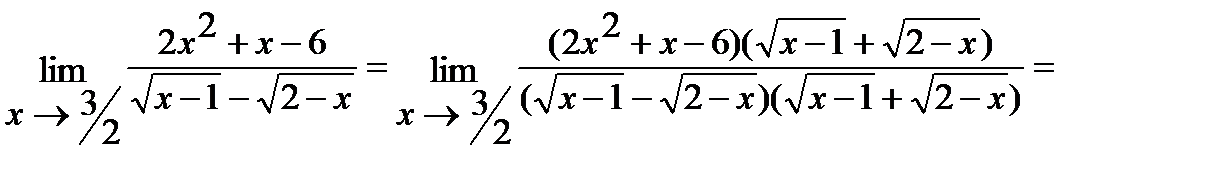
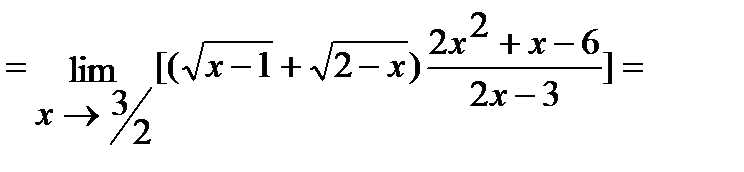
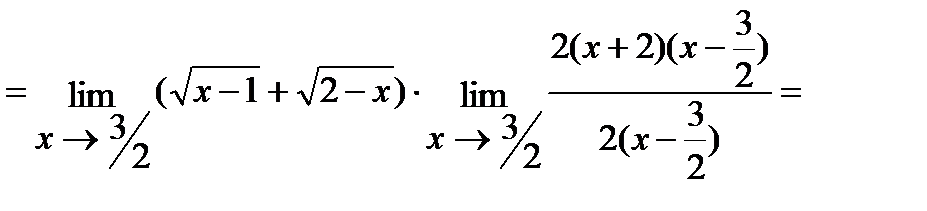
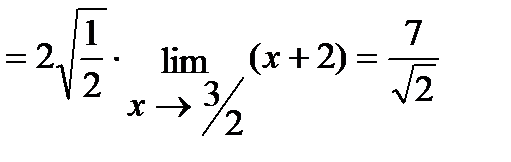 .
.
в) Для решения этой задачи воспользуемся первым замечательным пределом:
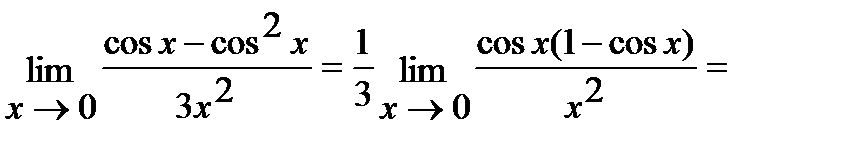
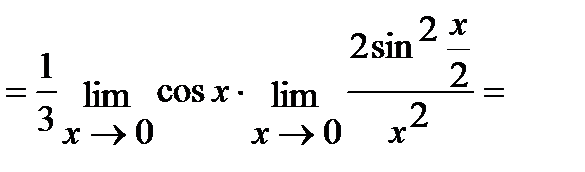
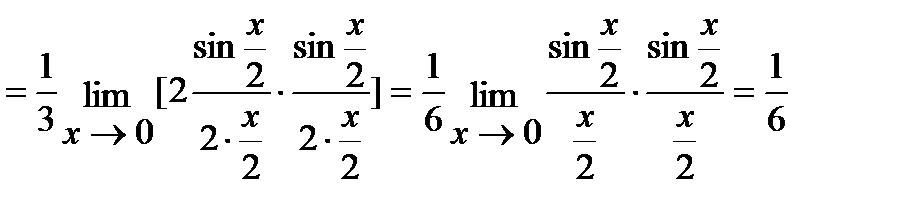
(Так как 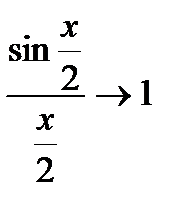 при
при 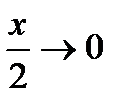 ).
).
г) Для решения данной задачи воспользуемся вторым замечательным пределом:
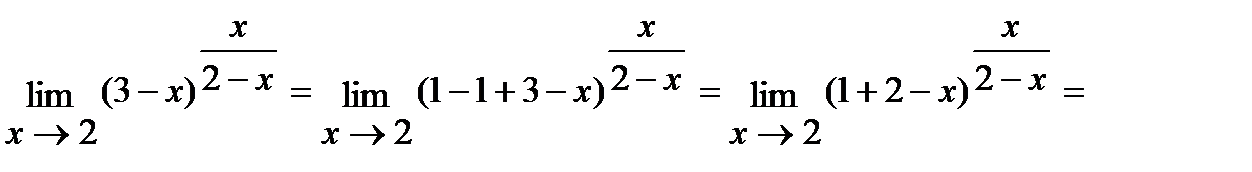
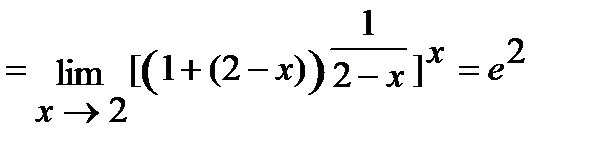 .
.
Последнее равенство вытекает из того, что в квадратной скобке стоит 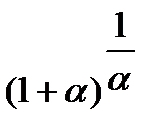 , где
, где 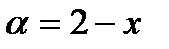 .
.
Решения задач е, ж аналогичны решению задачи а.
Например, задача ж имеет следующее решение:
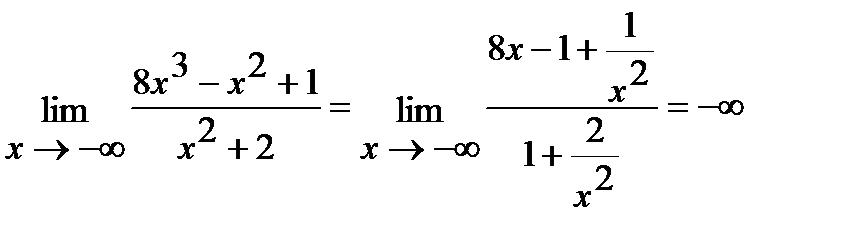 .
.
Производная функции
Производная функция 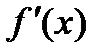 от функции
от функции 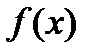 в данной точке
в данной точке 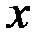 определяется равенством
определяется равенством
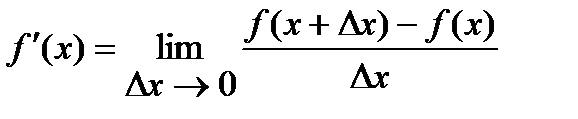 .
.
Таблица производных выглядит следующим образом:
1. 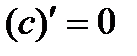 . 2.
. 2. 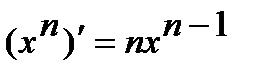 .
.
3. 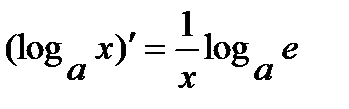 , в частности
, в частности 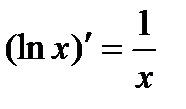 .
.
4. 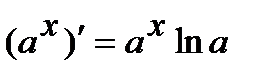 , в частности
, в частности 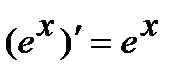 .
.
5. 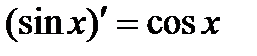 . 9.
. 9. 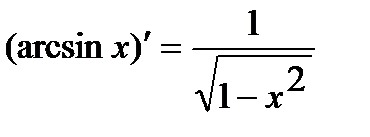 .
.
6. 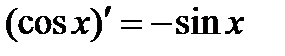 . 10.
. 10. 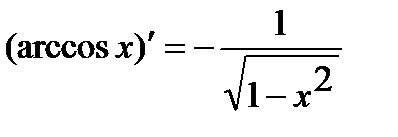 .
.
7. 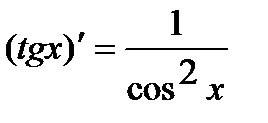 . 11.
. 11. 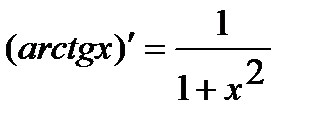 .
.
8. 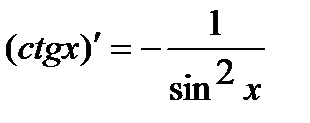 . 12.
. 12. 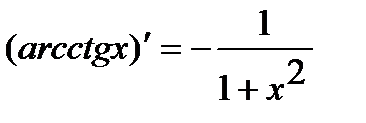 .
.
Основные правила дифференцирования
1. 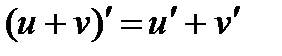 2.
2. 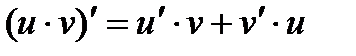 ,в частности,
,в частности,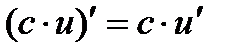 3.
3. 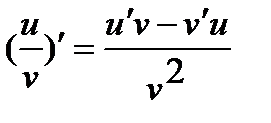 ,где
,где 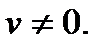
Задача. Найти производные следующих функций:
а) 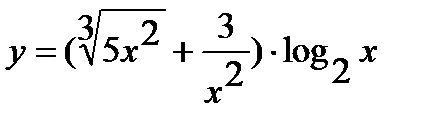 ; б)
; б) 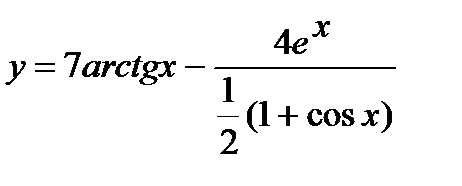 .
.
Решение.а) Преобразуем выражение в скобках, переходя к дробным и отрицательным показателям. Получим
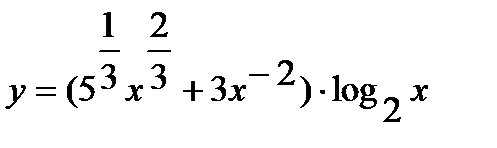 .
.
Используя правило дифференцирования произведения и суммы находим 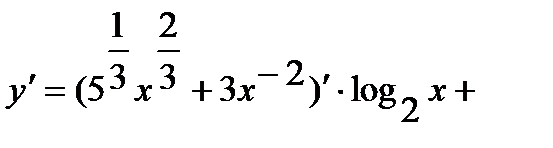
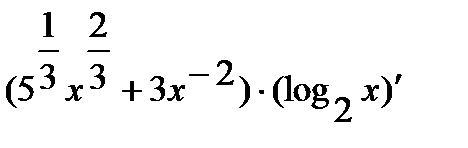 =
=
= 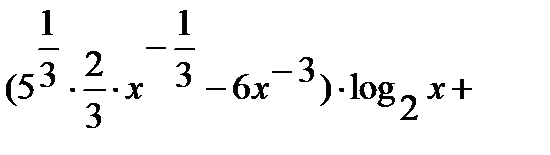
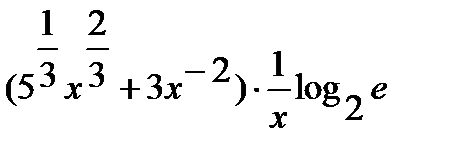 .
.
б) Проведем предварительное преобразование функции:
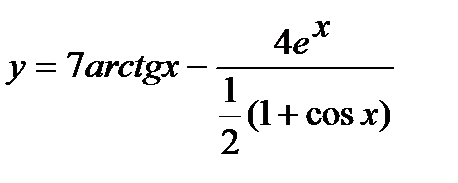 =
= 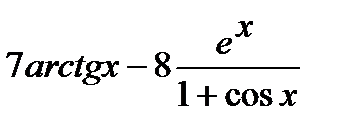 .
.
Используя правила дифференцирования произведения, суммы и частного, получим
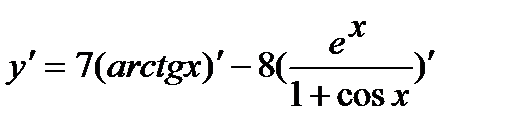 =
=
= 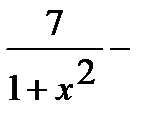
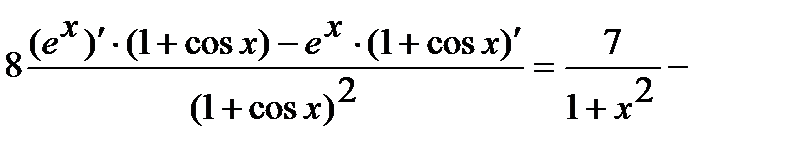
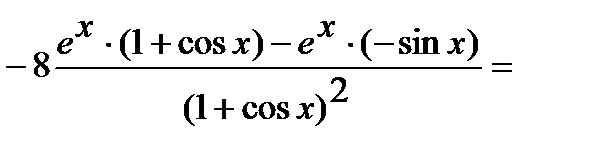
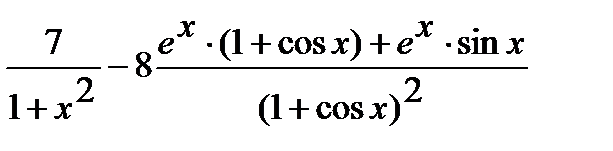 .
.
Дифференцирование сложной функции
Если функция 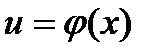 дифференцируема в точке
дифференцируема в точке 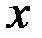 , а функция
, а функция 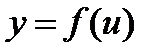 дифференцируема в точке
дифференцируема в точке 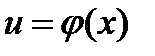 , то сложная функция
, то сложная функция 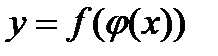 дифференцируема в точке
дифференцируема в точке 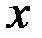 и
и
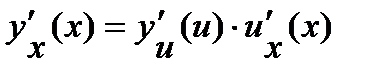 ,
,
где индекс внизу показывает, по какой переменной берется производная.
Задача. Найти производные следующих функций:
а) 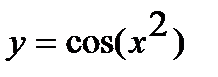 ; г)
; г) 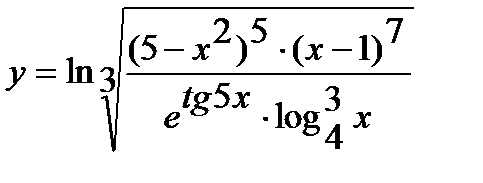 ;
;
б) 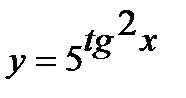 ;
;
в) 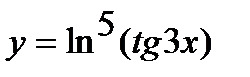 ;
;
Решение. а) Функцию 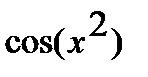 представим как композицию функций
представим как композицию функций 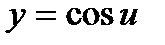 и
и 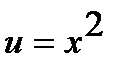 . Используя таблицу производных, находим:
. Используя таблицу производных, находим: 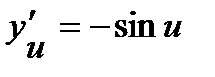 ,
, 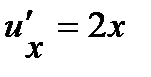 .
.
Тогда
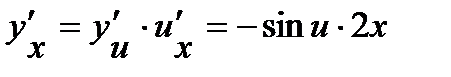
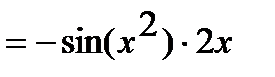 .
.
б) Функцию 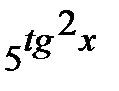 представим как композицию функций
представим как композицию функций 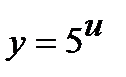 ,
,
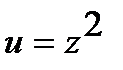 и
и 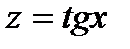 .Найдем производные по промежуточным аргументам:
.Найдем производные по промежуточным аргументам: 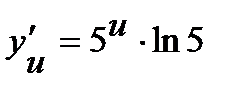 ,
, 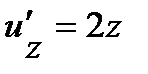 и
и 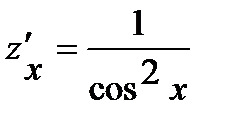 .
.
Производную сложной функции находим по формуле 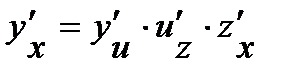 . Окончательно получим
. Окончательно получим 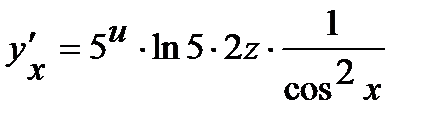 =
= 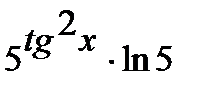
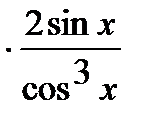 .
.
Аналогично решается задача в:
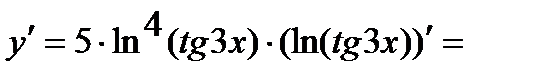
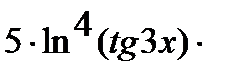
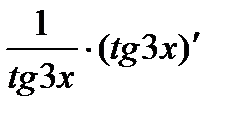 =
=
= 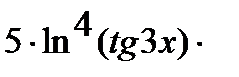
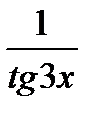

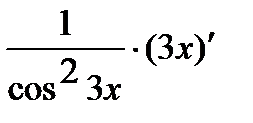 =
= 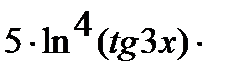
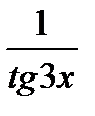
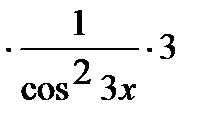 .
.
г) Предварительно упростив выражение, определяющее функцию, до вида
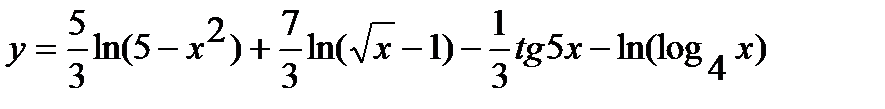 ,
,
находим производную:
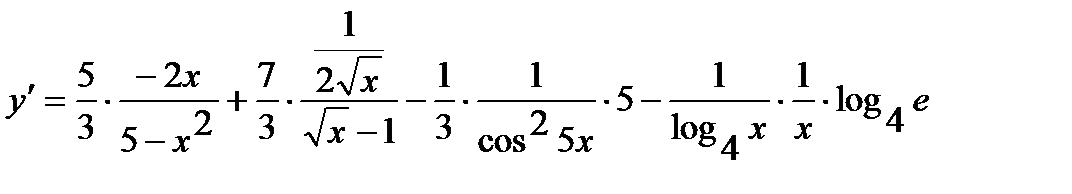 .
.
Методические указания к выполнению
Контрольной работы № 2
Приложение производной функции одной переменной
Теорема Лопиталя. Пусть функции 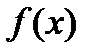 и
и 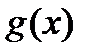 дифференцируемы в некоторой окрестности точки
дифференцируемы в некоторой окрестности точки 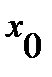 за исключением, может быть, самой точки
за исключением, может быть, самой точки 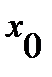 и непрерывны в этой окрестности (включая саму точку
и непрерывны в этой окрестности (включая саму точку 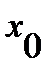 ), причем
), причем 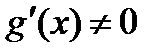 и
и 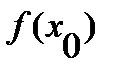 =
= 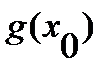 =0. Тогда, если существует
=0. Тогда, если существует 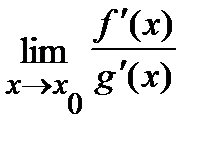 , то существует
, то существует 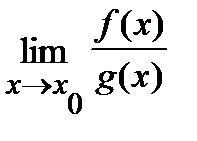 и эти пределы равны, то есть
и эти пределы равны, то есть
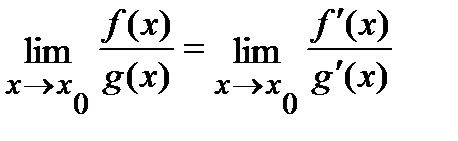 .
.
Таким образом, для нахождения предела 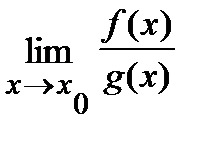 (для раскрытия неопределенности типа (
(для раскрытия неопределенности типа ( 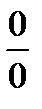 )) достаточно найти производные числителя и знаменателя дроби и вычислить предел
)) достаточно найти производные числителя и знаменателя дроби и вычислить предел 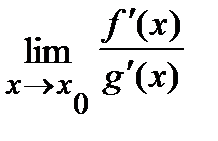 .
.
Такое же правило применяется при 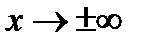 , а также для раскрытия неопределенностей типа (
, а также для раскрытия неопределенностей типа ( 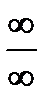 ).
).
Замечание. Если производные числителя и знаменателя в свою очередь стремятся к нулю или 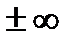 , то описанное правило применяется повторно и так далее.
, то описанное правило применяется повторно и так далее.
Пример.Вычислить 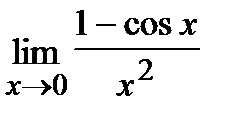 .
.
Решение.
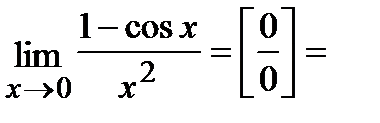
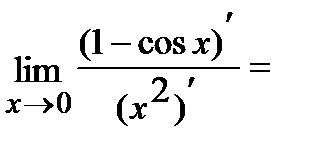
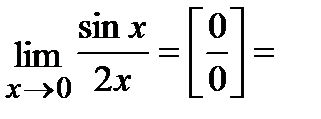
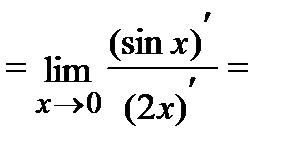
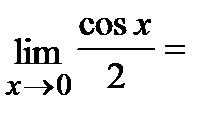
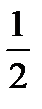 .
.
Пример.Вычислить 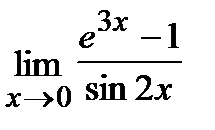 .
.
Решение.
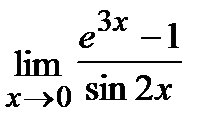 =
= 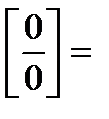
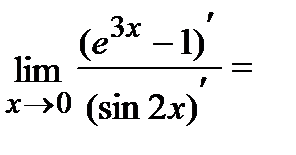
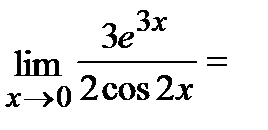
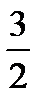 .
.
Если функция 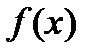 непрерывна на замкнутом промежутке
непрерывна на замкнутом промежутке 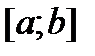 , то наибольшее и наименьшее значения она принимает или на концах этого отрезка, или в точках ее экстремума. Следовательно, для решения поставленной задачи надо найти значения функции на концах отрезка
, то наибольшее и наименьшее значения она принимает или на концах этого отрезка, или в точках ее экстремума. Следовательно, для решения поставленной задачи надо найти значения функции на концах отрезка 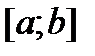 и в стационарных точках, принадлежащих этому отрезку. Затем из них выбрать наименьшее и наибольшее значения.
и в стационарных точках, принадлежащих этому отрезку. Затем из них выбрать наименьшее и наибольшее значения.
Пример.
Найти наибольшее и наименьшее значения функции 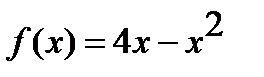 на отрезке
на отрезке 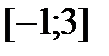 .
.
Решение. Определяем критические, или стационарные, точки функции 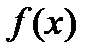 :
:
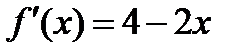 ;
; 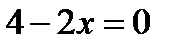 ;
; 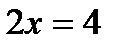 ;
; 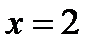 .
.
Рассматриваем только те стационарные точки, которые принадлежат отрезку 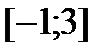 . Такой точкой является точка
. Такой точкой является точка 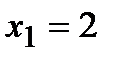 .
.
Вычисляем значения функции на концах промежутка и в точке 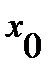 :
:
1) 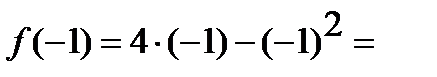
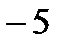 ;
;
2) 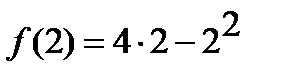 =
=  ;
;
3) 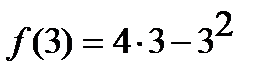 =
= 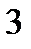 .
.
Ясно, что наибольшее значение функции будет равно  , которое она принимает в точке
, которое она принимает в точке 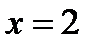 ; наименьшее значение принимается функцией в точке
; наименьшее значение принимается функцией в точке 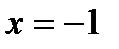 и равно
и равно 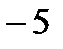 .
.
Общее исследование функций и построение их графиков удобно выполнять по следующей схеме:
1) Найти область определения функции.
2) Найти точки пересечения с осями координат.
3) Выяснить, не является ли функция четной или нечетной, периодической или непериодической.
4) Найти точки экстремума функции, вычислить значения функции в этих точках. Установить интервалы монотонности функции.
5) Найти точки перегиба графика функции, вычислить значения функции в этих точках. Установить интервалы выпуклости и вогнутости графика функции.
6) Найти асимптоты графика функции.
7) Используя результаты исследований, построить график функции.
Пример. Исследовать функцию 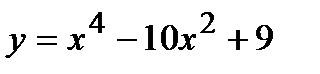 и построить ее график.
и построить ее график.
Решение.
1) Функция определена и непрерывна на всей оси. Итак, 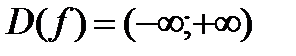 .
.
2) Найдем точки пересечения с осями координат.
а) с осью ОХ: 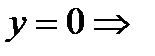
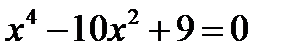
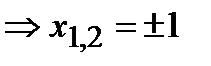 ,
, 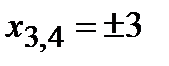 .
.
Следовательно, точки пересечения с осью ОХ- 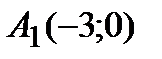 ,
, 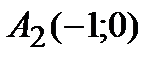 ,
, 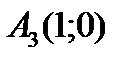 ,
, 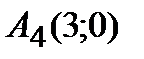 ;
;
б) с осью ОY: 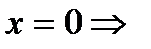
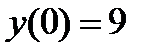 .
.
Следовательно, точка пересечения с осью ОY- 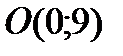 .
.
3) Функция четная, так как 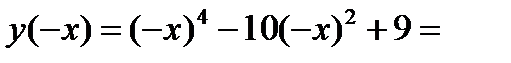
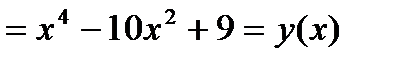 (поэтому ее график будет симметричен относительно оси OY).
(поэтому ее график будет симметричен относительно оси OY).
Функция непериодическая.
4) С помощью первой производной найдем промежутки возрастания и убывания функции.
Имеем 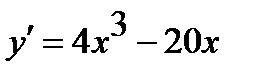 =0. Следовательно, точки
=0. Следовательно, точки 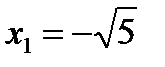 ,
, 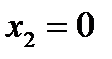 ,
, 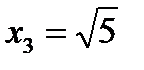 будут подозрительными на экстремум. Разбиваем всю область определения на промежутки
будут подозрительными на экстремум. Разбиваем всю область определения на промежутки 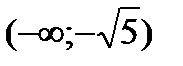 ,
, 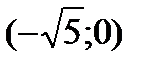 ,
, 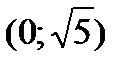 ,
, 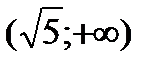 и исследуем функцию для
и исследуем функцию для 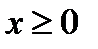 . Информация о поведении функции на интервале
. Информация о поведении функции на интервале 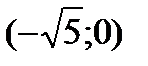 необходима для анализа функции в точке
необходима для анализа функции в точке 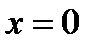 . По знаку производной определяем монотонность функции на каждом промежутке. Результаты исследований заносим в таблицу:
. По знаку производной определяем монотонность функции на каждом промежутке. Результаты исследований заносим в таблицу:
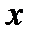 | 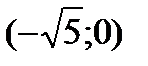 | 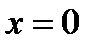 | 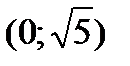 | 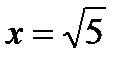 | 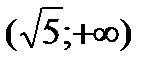 |
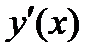 | 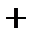 | 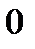 | 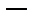 | 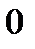 | 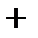 |
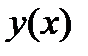 | Возрастает | 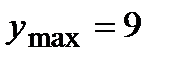 | Убывает | 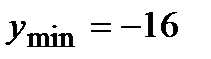 | Возрастает |
5) Чтобы исследовать функцию на выпуклость, найдем вторую производную: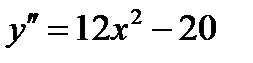 .Находим точки, в которых
.Находим точки, в которых 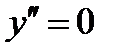 или
или 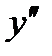 не существует.
не существует.
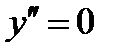 при
при 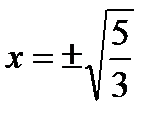 .
.
Исследуем знак второй производной на промежутках 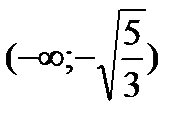 ,
, 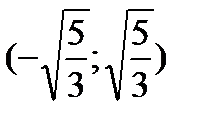 ,
, 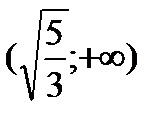 и результаты исследований представим в таблице:
и результаты исследований представим в таблице:
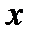 | 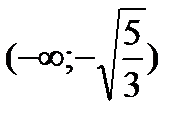 | 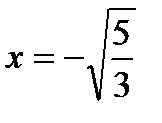 | 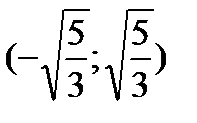 | 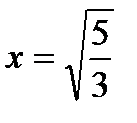 | 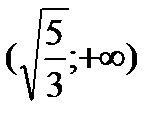 |
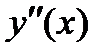 | 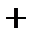 | 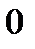 | 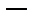 | 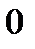 | 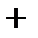 |
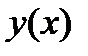 | Выпукла | Перегиб | Вогнута | Перегиб | Выпукла |
6) Вертикальных асимптот нет, поскольку область определения функции – вся числовая ось.
Найдем наклонную асимптоту 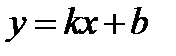 :
:
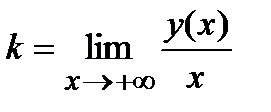 =
= 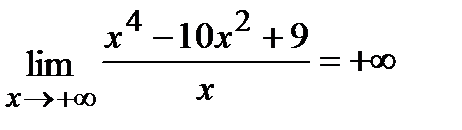 .
.
Следовательно, наклонных асимптот нет.
7) На основе проведенного исследования функции строим ее график (рис.1).
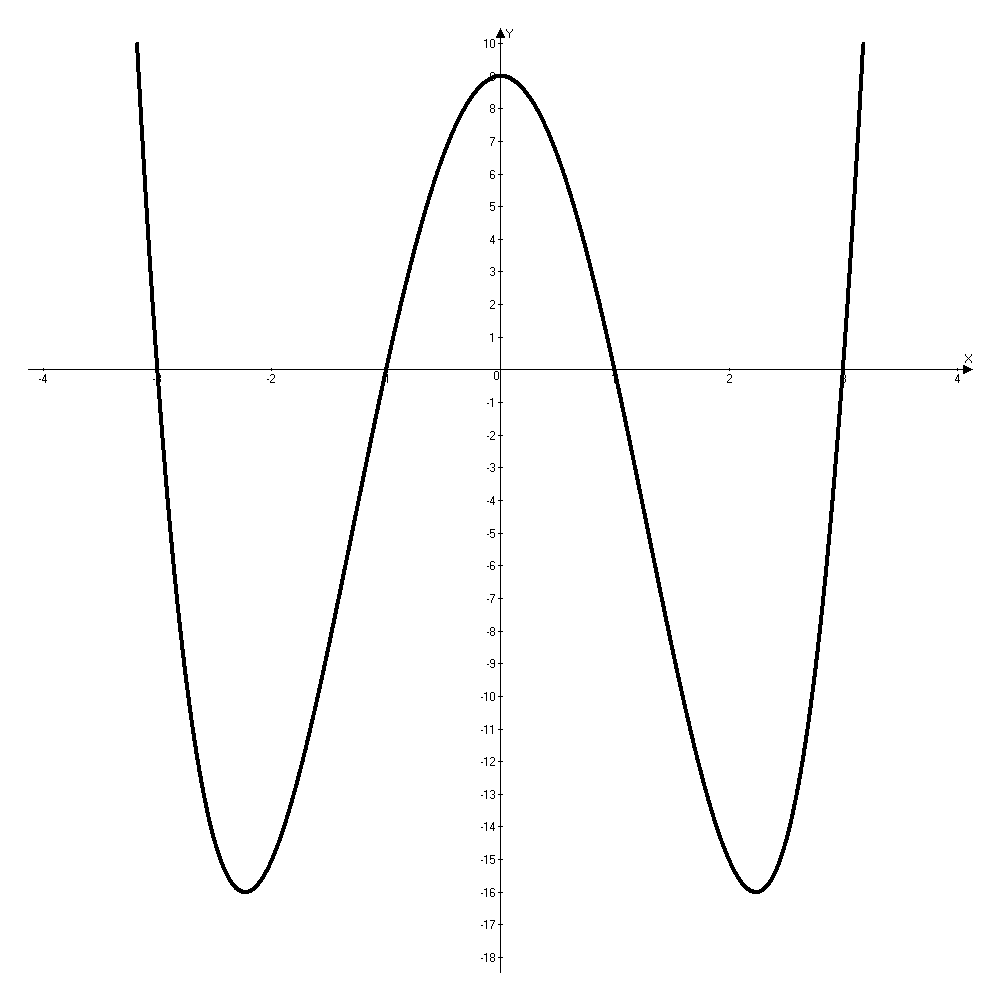
Рис. 1
Пример. Исследовать функцию 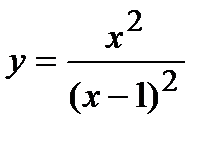 и построить ее график.
и построить ее график.
Решение.
1) Функция определена и непрерывна на всей оси, кроме точки 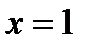 . Итак,
. Итак, 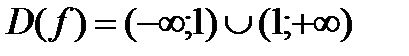 .
.
2) Найдем точки пересечения с осями координат.
а) с осью ОХ: 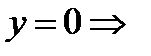
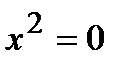
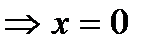 .
.
Следовательно, точка пересечения с осью ОХ- 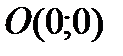 .
.
б) с осью ОY: 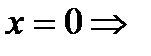
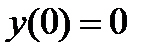 .
.
Следовательно, точка пересечения с осью ОY- 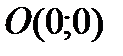 .
.
3) Функция общего вида, так как 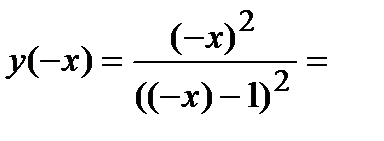
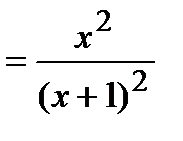 .
.
Функция непериодическая.
4) С помощью первой производной найдем промежутки возрастания и убывания функции.
Имеем 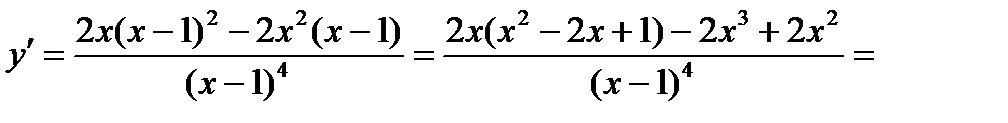
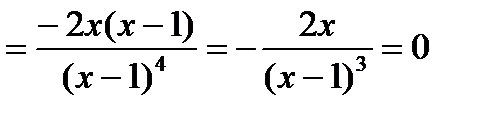 .
.
Следовательно, точка 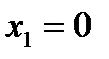 будет подозрительной на экстремум. Точка
будет подозрительной на экстремум. Точка 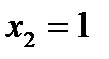 , в которой производная не существует, но в этой точке не существует и функция. Разбиваем всю область определения на промежутки
, в которой производная не существует, но в этой точке не существует и функция. Разбиваем всю область определения на промежутки 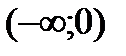 ,
, 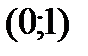 ,
, 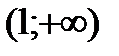 и исследуем функцию на указанных интервалах. По знаку производной определяем монотонность функции на каждом промежутке. Результаты исследований заносим в таблицу:
и исследуем функцию на указанных интервалах. По знаку производной определяем монотонность функции на каждом промежутке. Результаты исследований заносим в таблицу:
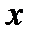 | 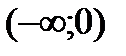 | 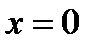 | 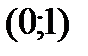 | 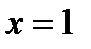 | 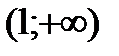 |
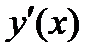 | 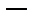 | 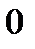 |  | нет |  |
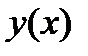 | Убывает | 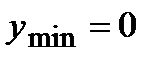 | Возрастает | нет | Убывает |
5) Чтобы исследовать функцию на выпуклость, найдем вторую производную:
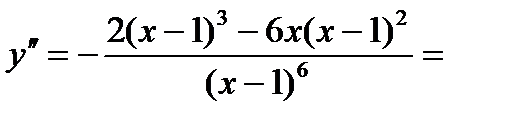
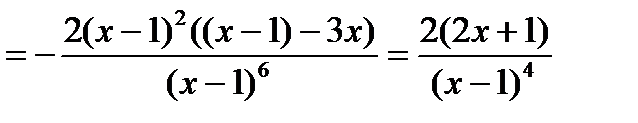 .
.
Находим точки, в которых 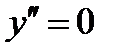 или
или 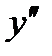 не существует:
не существует: 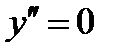 при
при 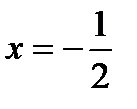 , не существует при
, не существует при 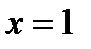 .Исследуем знак второй производной на промежутках
.Исследуем знак второй производной на промежутках 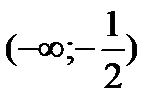 ,
, 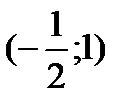 ,
, 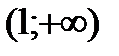 и результаты исследований представим в таблице:
и результаты исследований представим в таблице:
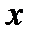 | 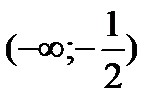 | 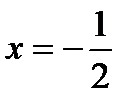 | 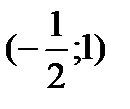 | 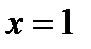 | 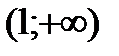 |
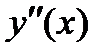 | 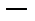 | 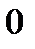 | 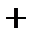 | нет | 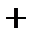 |
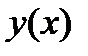 | Вогнута | Перегиб | Выпукла | нет | Выпукла |
6) Найдем вертикальные асимптоты:
Исследуем поведение функции в окрестности точки 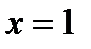 :
:
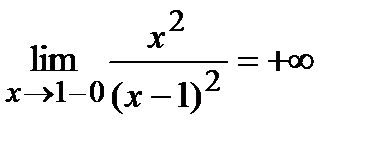 ;
; 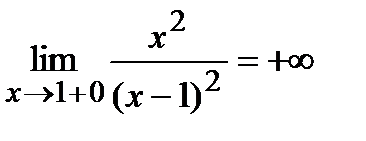 .
.
Пределы не конечны, следовательно, вертикальная асимптота имеет вид: 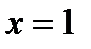 .
.
Найдем наклонную асимптоту 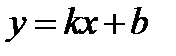 :
:
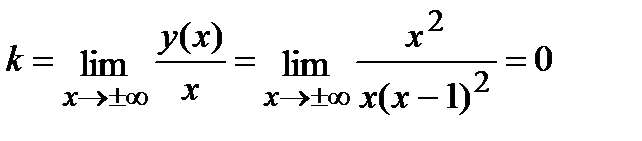 ;
;
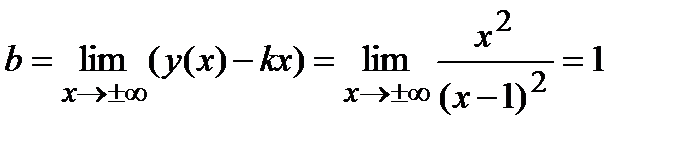 .
.
Следовательно, наклонная асимптота: 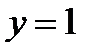 .
.
7) На основе проведенного исследования функции строим ее график (рис.2).
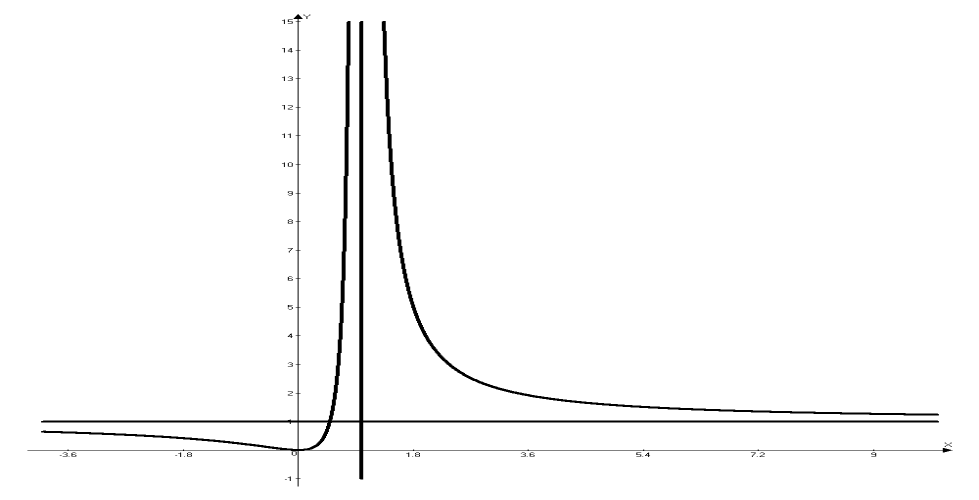
Рис. 2
Неопределенный интеграл
Функция 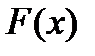 называется первообразной функции
называется первообразной функции 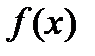 на некотором интервале
на некотором интервале 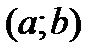 , если
, если 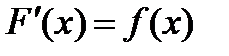 для всех значений
для всех значений 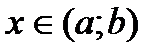 . Если
. Если 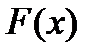 — первообразная
— первообразная 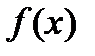 , то очевидно, что бесконечное множество всех первообразных
, то очевидно, что бесконечное множество всех первообразных 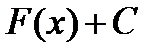 , отличающихся только константой, также будет первообразной
, отличающихся только константой, также будет первообразной 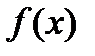 . Множество всех первообразных функций
. Множество всех первообразных функций 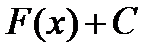
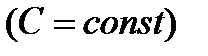 называется неопределенным интеграломот функции
называется неопределенным интеграломот функции 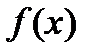 и обозначается
и обозначается 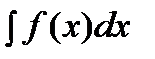 . При этом
. При этом 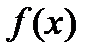 называется подынтегральной функцией,
называется подынтегральной функцией, 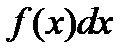 — подынтегральным выражением,
— подынтегральным выражением, 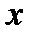 — переменной интегрирования.
— переменной интегрирования.
Согласно вышеприведенному:
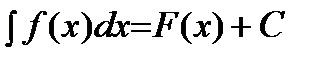 ,
,
где 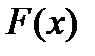 — некоторая первообразная функции
— некоторая первообразная функции 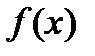 ;
; 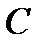 — произвольная постоянная.
— произвольная постоянная.
Неопределенный интеграл обладает следующими свойствами:
1) 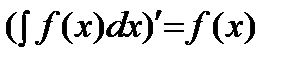 .
.
2) 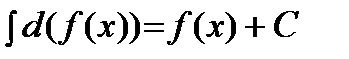 .
.
3) 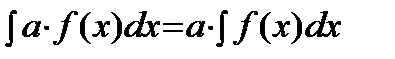 , где
, где 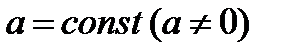 .
.
4) 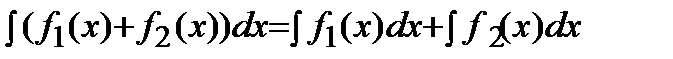 .
.
5) 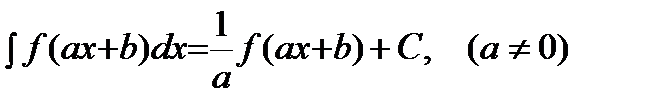 .
.
Таблица основных неопределенных интегралов:
1) 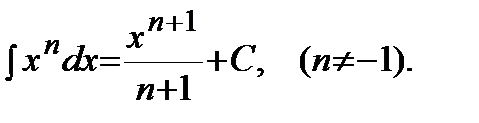 | 2) 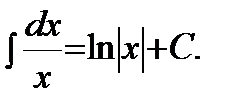 |
3) 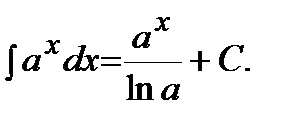 | 4) 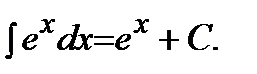 |
5) 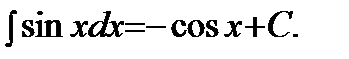 | 6) 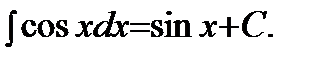 |
7) 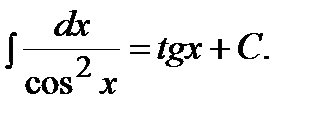 | 8) 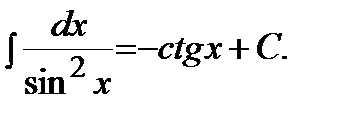 |
9) 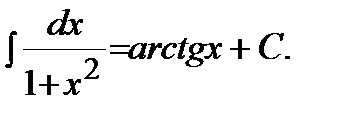 | 10) 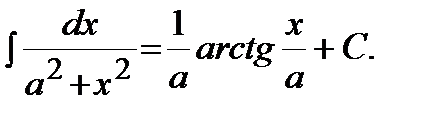 |
11) 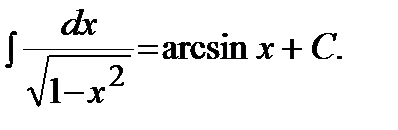 | 12) 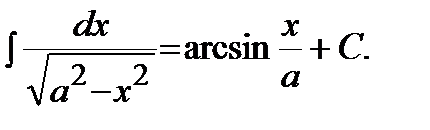 |
13) 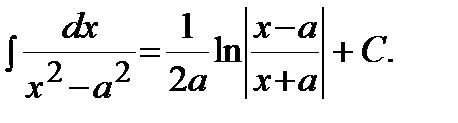 | 14) 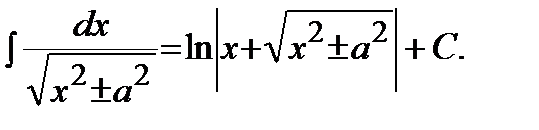 |
