Метод Фурье решения смешанных задач для уравнения колебаний струны
Для решения смешанных задач во многих случаях используется так называемый метод Фурье или метод разделения переменных. В настоящем параграфе применение этого метода мы рассмотрим на примере смешанных задач для уравнения колебаний струны (2.8).
6.1. Случай свободных колебаний. Однородные граничные условия.Требуется найти решение уравнения
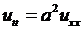 (6.1)
(6.1)
при граничных условиях
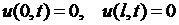 (6.2)
(6.2)
и начальных условиях
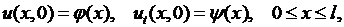 (6.3)
(6.3)
где 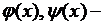 заданные функции.
заданные функции.
Метод Фурье решения задачи состоит в следующем.
I. Сначала находим частные решения уравнения (6.1), удовлетворяющие граничным условиям (6.2). Их будем искать в виде
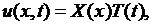 (6.4)
(6.4)
где 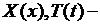 неизвестные функции одной переменной. С целью определения
неизвестные функции одной переменной. С целью определения 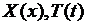 функцию (6.4) подставим в уравнение (6.1). Получим
функцию (6.4) подставим в уравнение (6.1). Получим
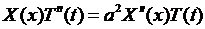 ,
,
откуда, разделяя переменные, будем иметь:
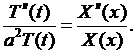 (6.5)
(6.5)
Соотношение (6.5) должно удовлетворяться тождественно при 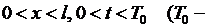 произвольно фиксированное положительное число). Зафиксировав произвольно
произвольно фиксированное положительное число). Зафиксировав произвольно 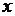 в правой части (6.5) и меняя
в правой части (6.5) и меняя 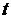 в левой части, приходим к выводу, что левая часть соотношения (6.5) необходимо должна равняться постоянной; этой же постоянной должна равняться и правая часть. Обозначая эту постоянную через
в левой части, приходим к выводу, что левая часть соотношения (6.5) необходимо должна равняться постоянной; этой же постоянной должна равняться и правая часть. Обозначая эту постоянную через 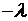 , будем иметь:
, будем иметь:
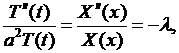
откуда получим два обыкновенных дифференциальных уравнения относительно функций 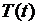 и
и 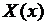 :
:
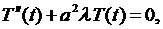 (6.6)
(6.6)
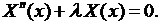 (6.7)
(6.7)
Таким образом, уравнение (6.1) распалось на два уравнения (6.6), (6.7), из которых одно содержит функцию только от 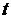 , а другое – функцию только от
, а другое – функцию только от 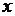 , или, как говорят, в уравнении (6.1) переменные разделились.
, или, как говорят, в уравнении (6.1) переменные разделились.
Теперь функцию (6.4) подставим в граничные условия (6.2). Получим
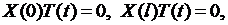
откуда
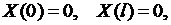 (6.8)
(6.8)
так как случай 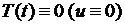 интереса не представляет. Таким образом, переменные разделились также и в граничных условиях.
интереса не представляет. Таким образом, переменные разделились также и в граничных условиях.
Для определения функции 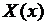 мы пришли к следующей граничной задаче для обыкновенного дифференциального уравнения второго порядка.
мы пришли к следующей граничной задаче для обыкновенного дифференциального уравнения второго порядка.
Задача Штурма- Лиувилля.Найти такие значения параметра 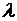 , называемые собственными значениями,при которых существуют нетривиальные (т.е.не равные нулю тождественно) решения уравнения (6.7), удовлетворяющие граничным условиям (6.8), а также найти эти решения, называемые собственными функциями.
, называемые собственными значениями,при которых существуют нетривиальные (т.е.не равные нулю тождественно) решения уравнения (6.7), удовлетворяющие граничным условиям (6.8), а также найти эти решения, называемые собственными функциями.
Найдем решение этой задачи. Уравнение (6.7) есть уравнение с постоянными коэффициентами; для его решения надо составить характеристическое уравнение
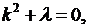
корни которого 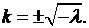 Следовательно, вид решения зависит от знака
Следовательно, вид решения зависит от знака 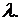
а) Пусть 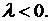 Общее решение уравнения (6.7) в этом случае имеет вид:
Общее решение уравнения (6.7) в этом случае имеет вид:
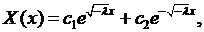
где 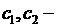 произвольные постоянные. Подставляя его в граничные условия (6.8), будем иметь:
произвольные постоянные. Подставляя его в граничные условия (6.8), будем иметь:
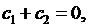
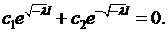
Относительно 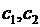 мы получили однородную систему линейных алгебраических уравнений. Так как ее определитель не равен нулю, система имеет только нулевое решение. Поэтому задача Штурма- Лиувилля в этом случае неразрешима.
мы получили однородную систему линейных алгебраических уравнений. Так как ее определитель не равен нулю, система имеет только нулевое решение. Поэтому задача Штурма- Лиувилля в этом случае неразрешима.
б) Пусть 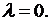 Общее решение уравнения (6.7) имеет вид
Общее решение уравнения (6.7) имеет вид 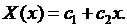 Из условий (6.8) получаем
Из условий (6.8) получаем 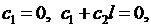 откуда
откуда 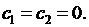 Поэтому задача Штурма- Лиувилля также неразрешима.
Поэтому задача Штурма- Лиувилля также неразрешима.
в) Пусть 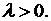 В этом случае общее решение уравнения (6.7) дается формулой
В этом случае общее решение уравнения (6.7) дается формулой
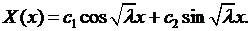 (6.9)
(6.9)
Подстановка (6.9) в граничные условия (6.8) дает
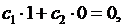
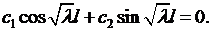 (6.10)
(6.10)
Система (6.10) имеет ненулевое решение только тогда, когда ее определитель равен нулю. Так как определитель системы (6.10) равен 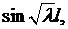 то приравнивая его к нулю, для определения значений
то приравнивая его к нулю, для определения значений 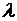 получаем уравнение
получаем уравнение
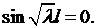
Решая его, находим корни 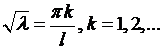 , следовательно, собственные значения задачи Штурма- Лиувилля имеют вид:
, следовательно, собственные значения задачи Штурма- Лиувилля имеют вид:
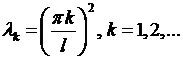 (6.11)
(6.11)
Подставляя значения (6.11) вместо 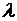 в систему (6.10), будем иметь:
в систему (6.10), будем иметь: 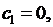 а
а 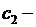 произвольное. В дальнейшем будем считать, что
произвольное. В дальнейшем будем считать, что 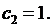 Внося все это в (6.9), получаем собственные функции задачи (6.7), (6.8):
Внося все это в (6.9), получаем собственные функции задачи (6.7), (6.8):
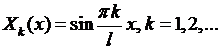 (6.12)
(6.12)
Решаем теперь уравнение (6.6) при 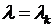 , т.е. уравнение
, т.е. уравнение
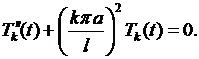
Общее его решение имеет вид:
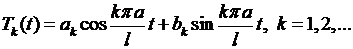 (6.13)
(6.13)
где 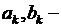 произвольные постоянные.
произвольные постоянные.
Подставив функции (6.12),(6.13) в (6.4), получим бесконечную последовательность частных решений уравнения (6.1), удовлетворяющих граничным условиям (6.2):
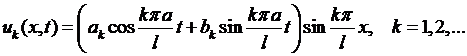 (6.14)
(6.14)
II. Теперь построим решение, удовлетворяющее еще и заданным начальным условиям (6.3). С этой целью образуем бесконечный ряд из частных решений (6.14):
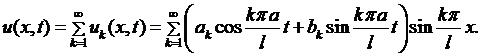 (6.15)
(6.15)
В дальнейшем будем предполагать, что ряд (6.15) сходится равномерно в области 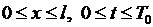 и допускает двукратное почленное дифференцирование по переменным
и допускает двукратное почленное дифференцирование по переменным 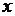 и
и 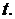 Ясно, что для этого нужно, чтобы функции
Ясно, что для этого нужно, чтобы функции 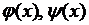 удовлетворяли определенным условиям. Достаточно, например, выполнения следующих требований:
удовлетворяли определенным условиям. Достаточно, например, выполнения следующих требований:
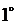 )
) 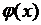 дважды непрерывно дифференцируема на
дважды непрерывно дифференцируема на 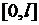 , третья производная кусочно непрерывно дифференцируема на
, третья производная кусочно непрерывно дифференцируема на 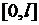 и
и
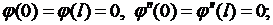
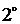 )
) 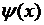 непрерывно дифференцируема на
непрерывно дифференцируема на 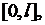 вторая производная кусочно непрерывна на
вторая производная кусочно непрерывна на 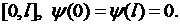
Тогда в силу линейности и однородности уравнения (6.1) сумма ряда (6.15) из его решений также будет решением уравнения (6.1). Кроме того, поскольку каждое слагаемое ряда удовлетворяет однородным граничным условиям (6.2), то сумма ряда будет удовлетворять и этим условиям.
Покажем, что постоянные 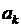 и
и 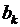 в (6.15) можно определить так, чтобы удовлетворялись и начальные условия (6.3). Продифференцируем ряд (6.15) по
в (6.15) можно определить так, чтобы удовлетворялись и начальные условия (6.3). Продифференцируем ряд (6.15) по 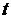 :
:
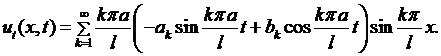 (6.16)
(6.16)
Подставляя (6.15),(6.16) в (6.3), получаем
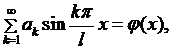
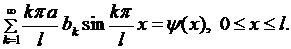 (6.17)
(6.17)
Соотношения (6.17) представляют собой разложения функций 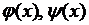 в ряд Фурье по синусам. Из теории тригонометрических рядов Фурье известно, что всякая функция
в ряд Фурье по синусам. Из теории тригонометрических рядов Фурье известно, что всякая функция 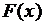 , непрерывная на отрезке
, непрерывная на отрезке 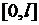 вместе со своей производной первого порядка и удовлетворяющая условию
вместе со своей производной первого порядка и удовлетворяющая условию 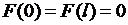 , разлагается в абсолютно и равномерно сходящийся ряд Фурье по синусам:
, разлагается в абсолютно и равномерно сходящийся ряд Фурье по синусам:
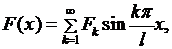
где
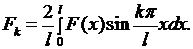
Заметим, что функции 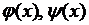 удовлетворяют указанным условиям. Поэтому соотношения действительно будут выполняться, если постоянные
удовлетворяют указанным условиям. Поэтому соотношения действительно будут выполняться, если постоянные 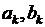 имеют вид:
имеют вид:
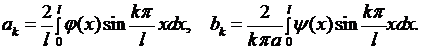 (6.18)
(6.18)
Подставляя (6.18) в (6.15), получаем решение смешанной задачи (6.1)-(6.3).
Таким образом, решение задачи (6.1)- (6.3) дается формулой (6.15), в которой постоянные 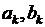 определены соотношениями (6.18).
определены соотношениями (6.18).
Рассмотрим физическую интерпретацию решения (6.15). Если ввести обозначения 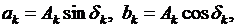 то это решение можно записать в виде
то это решение можно записать в виде
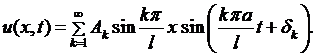 (6.19)
(6.19)
Каждый член этого ряда представляет собой так называемую стоячую волну,при которой точки струны совершают гармоническое колебательное движение с одинаковой фазой 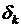 , с амплитудой
, с амплитудой 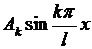 и частотой
и частотой 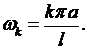 При таком колебании струна будет издавать звук, высота которого зависит от частоты колебаний
При таком колебании струна будет издавать звук, высота которого зависит от частоты колебаний 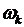 . Частота основного (самого низкого) тона выражается формулой
. Частота основного (самого низкого) тона выражается формулой 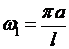 . Остальные тона, соответствующие частотам, кратным
. Остальные тона, соответствующие частотам, кратным 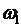 , называются гармониками. Решение (6.19) складывается из отдельных гармоник; амплитуда их, а поэтому и влияние их на интенсивность звука, издаваемого струной, обыкновенно быстро убывает при увеличении номера гармоники и все их действие сводится к созданию тембра звука. Приведенная интерпретация решения подтверждается экспериментально: с помощью резонаторов можно выделять гармоники, соответствующие различным значениям
, называются гармониками. Решение (6.19) складывается из отдельных гармоник; амплитуда их, а поэтому и влияние их на интенсивность звука, издаваемого струной, обыкновенно быстро убывает при увеличении номера гармоники и все их действие сводится к созданию тембра звука. Приведенная интерпретация решения подтверждается экспериментально: с помощью резонаторов можно выделять гармоники, соответствующие различным значениям 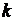 .
.
6.2. Случай вынужденных колебаний. Однородные граничные условия.Найти решение уравнения
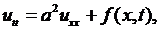 (6.20)
(6.20)
удовлетворяющее граничным условиям
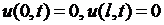 (6.21)
(6.21)
и начальным условиям
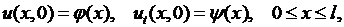 (6.22)
(6.22)
где 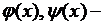 заданные функции.
заданные функции.
Эту задачу разобьем на две более простые. Для этого решение представим в виде
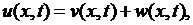 (6.23)
(6.23)
где 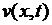 есть решение задачи
есть решение задачи
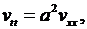 (6.24)
(6.24)
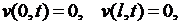 (6.25)
(6.25)
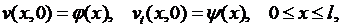 (6.26)
(6.26)
а 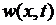 есть решение задачи
есть решение задачи
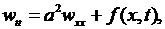 (6.27)
(6.27)
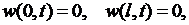 (6.28)
(6.28)
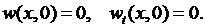 (6.29)
(6.29)
Задача (6.24)- (6.26) для функции 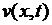 рассмотрена нами в пункте 6.1; ее решение дается рядом (6.15). Решение
рассмотрена нами в пункте 6.1; ее решение дается рядом (6.15). Решение 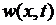 задачи (6.27)- (6.29) будем искать в виде
задачи (6.27)- (6.29) будем искать в виде
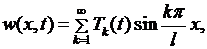 (6.30)
(6.30)
где 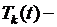 неизвестные функции.
неизвестные функции.
Пусть ряд (6.30) равномерно сходится в области 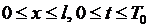 и допускает почленное двукратное дифференцирование по
и допускает почленное двукратное дифференцирование по 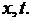 Тогда, подставляя (6.30) в (6.27), получаем
Тогда, подставляя (6.30) в (6.27), получаем
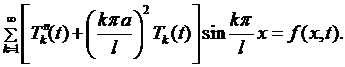 (6.31)
(6.31)
При произвольно фиксированном 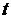 (6.31) представляет собой разложение функции
(6.31) представляет собой разложение функции 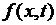 в ряд Фурье по синусам. Поэтому для коэффициентов разложения (выражений в квадратных скобках) имеем
в ряд Фурье по синусам. Поэтому для коэффициентов разложения (выражений в квадратных скобках) имеем
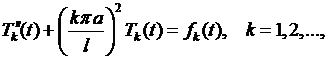 (6.32)
(6.32)
где
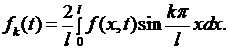 (6.33)
(6.33)
С учетом (6.30) и 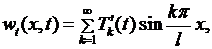 из условий (6.29) получим
из условий (6.29) получим
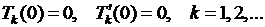 (6.34)
(6.34)
Следовательно, для определения функций 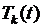 имеем задачу (6.32), (6.34), представляющую задачу Коши для обыкновенного дифференциального уравнения второго порядка с постоянными коэффициентами (6.32) с начальными условиями (6.34). Ее решение может быть получено с помощью метода вариации произвольных постоянных в следующем виде
имеем задачу (6.32), (6.34), представляющую задачу Коши для обыкновенного дифференциального уравнения второго порядка с постоянными коэффициентами (6.32) с начальными условиями (6.34). Ее решение может быть получено с помощью метода вариации произвольных постоянных в следующем виде
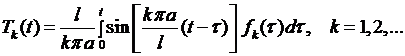 (6.35)
(6.35)
Подставляя сюда вместо 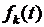 выражение (6.33), а затем полученный результат в (6.30), получаем решение задачи (6.27)- (6.29). Решение исходной задачи (6.20)- (6.22) найдем по формуле (6.23).
выражение (6.33), а затем полученный результат в (6.30), получаем решение задачи (6.27)- (6.29). Решение исходной задачи (6.20)- (6.22) найдем по формуле (6.23).
6.3. Случай вынужденных колебаний. Неоднородные граничные условия.Рассмотрим задачу: найти решение уравнения
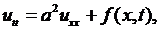 (6.36)
(6.36)
удовлетворяющее граничным условиям
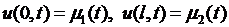 (6.37)
(6.37)
и начальным условиям
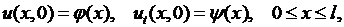 (6.38)
(6.38)
где 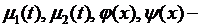 заданные функции.
заданные функции.
Решение этой задачи будем искать в виде
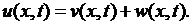 (6.39)
(6.39)
От функции 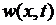 потребуем, чтобы она имела непрерывные вторые производные по
потребуем, чтобы она имела непрерывные вторые производные по 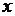 и
и 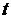 и удовлетворяла ненулевым граничным условиям
и удовлетворяла ненулевым граничным условиям
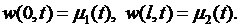 (6.40)
(6.40)
Такую функцию всегда можно найти, например,
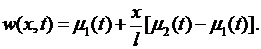
Считая теперь функцию 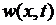 известной, выведем задачу для функции
известной, выведем задачу для функции 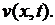 Подставляя (6.39) в уравнение (6.36), получаем
Подставляя (6.39) в уравнение (6.36), получаем
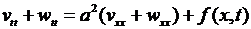
или
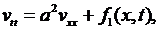 (6.41)
(6.41)
где принято обозначение 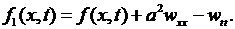
Далее, с учетом (6.37), (6.40) и соотношения 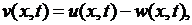 вытекающего из (6.39), для
вытекающего из (6.39), для 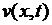 получаем однородные граничные условия
получаем однородные граничные условия
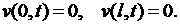 (6.42)
(6.42)
Наконец, учитывая (6.38), будем иметь:
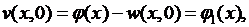
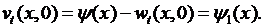 (6.43)
(6.43)
Таким образом, для определения функции 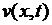 мы пришли к задаче (6.41)- (6.43) для уравнения вынужденных колебаний струны с однородными граничными условиями; эта задача была рассмотрена нами в пункте 6.2.
мы пришли к задаче (6.41)- (6.43) для уравнения вынужденных колебаний струны с однородными граничными условиями; эта задача была рассмотрена нами в пункте 6.2.
Пример 6.1.Решить методом Фурье смешанную краевую задачу для уравнения свободных колебаний струны:
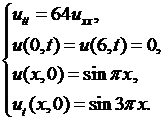
Решение.Решение этой задачи дается формулой (6.15), в которой коэффициенты 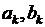 определены соотношениями (6.18). В нашем случае
определены соотношениями (6.18). В нашем случае
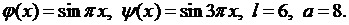 Внося эти данные в (6.18), получаем
Внося эти данные в (6.18), получаем
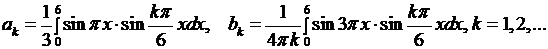
Вычислим интегралы:
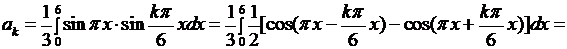
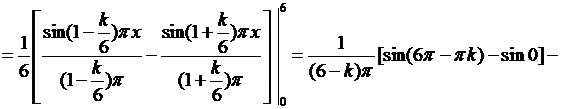
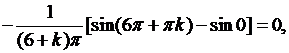 если
если 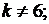
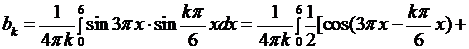
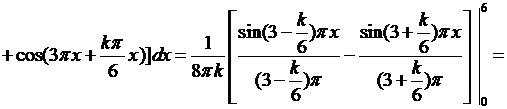
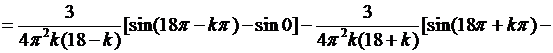
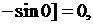 если
если 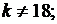
при 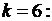
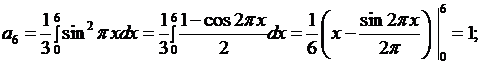
при 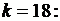
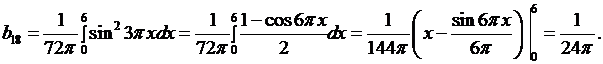
Подставив эти значения коэффициентов 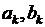 в (6.15), получим решение задачи в следующем виде
в (6.15), получим решение задачи в следующем виде
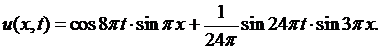
Покажем, что коэффициенты 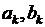 в некоторых случаях, как, например, в этом примере, можно найти и другим способом, не прибегая к формулам (6.18). Для этого функцию
в некоторых случаях, как, например, в этом примере, можно найти и другим способом, не прибегая к формулам (6.18). Для этого функцию 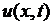 в виде (6.15) и ее производную
в виде (6.15) и ее производную 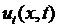 в виде (6.16) подставим в начальные условия:
в виде (6.16) подставим в начальные условия:
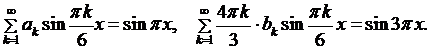
В правых частях этих равенств стоят разложения в ряд Фурье по синусам с известными коэффициентами. Поэтому приравнивая коэффициенты при 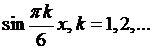 , получаем систему
, получаем систему
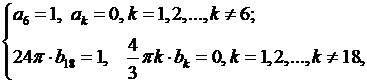
откуда 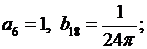 остальные
остальные 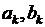 равны нулю.
равны нулю.
Пример 6.2.Решить методом Фурье смешанную краевую задачу для уравнения вынужденных колебаний струны:
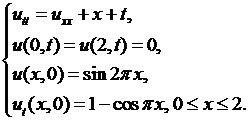
Решение. В соответствии с изложенным в разделе 6.2 §6 решение этой задачи ищется в виде
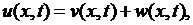 (6.44)
(6.44)
где 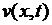 есть решение задачи
есть решение задачи
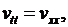
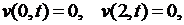
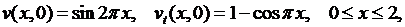
а 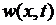 есть решение задачи
есть решение задачи
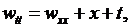
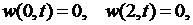
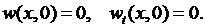
Сначала решаем задачу относительно функции 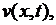 решение которой дается формулой (6.15), в которой коэффициенты
решение которой дается формулой (6.15), в которой коэффициенты 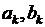 определены соотношениями (6.18). В нашем случае
определены соотношениями (6.18). В нашем случае
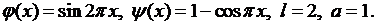
Внося эти данные в (6.18), получаем
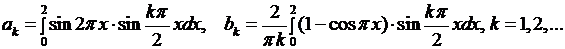
Вычислим интегралы:
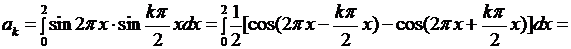
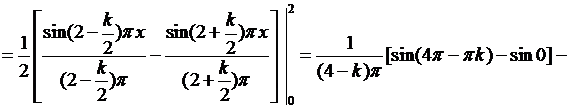
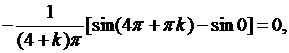 если
если 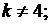
при 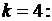
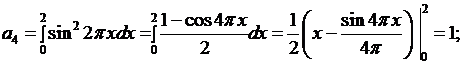
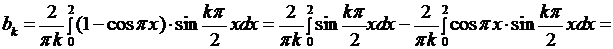
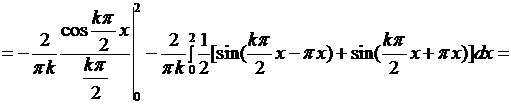
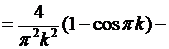
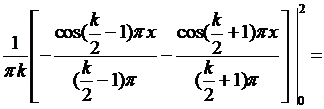
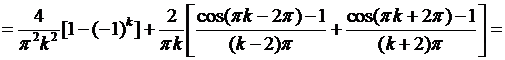
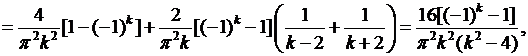
если 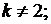
при 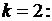
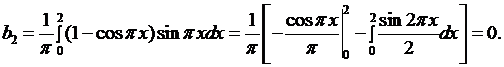
Таким образом, все коэффициенты 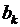 с четными номерами равны нулю. Подставив найденные значения коэффициентов
с четными номерами равны нулю. Подставив найденные значения коэффициентов 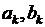 в (6.15), получим решение первой задачи относительно
в (6.15), получим решение первой задачи относительно 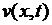 в следующем виде
в следующем виде
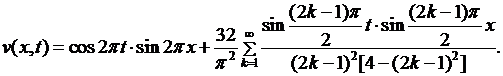 (6.45)
(6.45)
Перейдем к решению задачи относительно функции 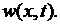 Ее ищем в виде (6.30), где
Ее ищем в виде (6.30), где 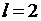 и функции
и функции 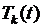 определяются формулой (6.35), которая в нашем случае примет вид:
определяются формулой (6.35), которая в нашем случае примет вид:
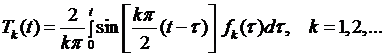 , (6.46)
, (6.46)
где для 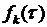 в силу (6.33) с учетом
в силу (6.33) с учетом 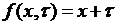 получаем
получаем
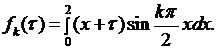
Вычислим интеграл: 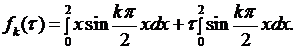 Первый интеграл в этой сумме вычисляется по частям:
Первый интеграл в этой сумме вычисляется по частям:
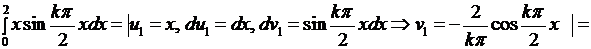
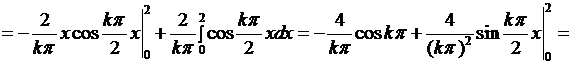
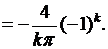
Второй интеграл равен 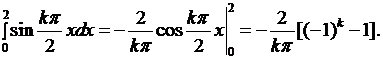
Следовательно, 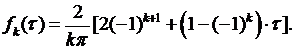 Внося это выражение в (6.46), для
Внося это выражение в (6.46), для 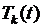 интегрированием по частям получаем
интегрированием по частям получаем
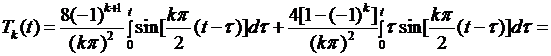
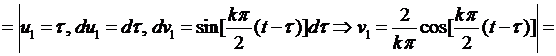
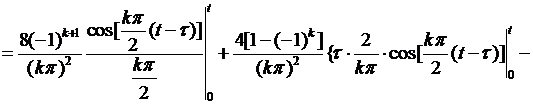
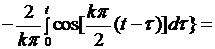
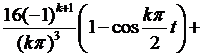
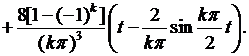 (6.47)
(6.47)
Теперь, если (6.47) подставить в (6.30), то получим решение второй задачи 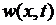 , которое вместе с (6.45) по формуле (6.44) дает решение исходной задачи.
, которое вместе с (6.45) по формуле (6.44) дает решение исходной задачи.
Задачи
Методом Фурье найти решения следующих смешанных задач для уравнения колебаний струны:
6.1. 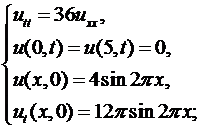 6.2.
6.2. 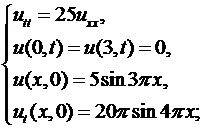
6.3. 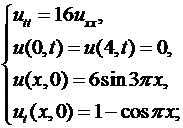 6.4.
6.4. 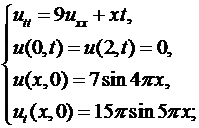
6.5. 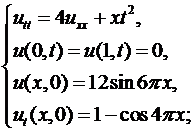 6.6.
6.6.