Ряды с членами произвольного знака.

Знакопеременным называется ряд, членами которого являются действительные числа произвольного знака.

Определение. Знакопеременный ряд ( а также ряд с комплексными членами ) называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов.

Для исследования рядов на абсолютную сходимость, очевидно, надо пользоваться признаками сходимости рядов с положительными членами.

Определение. Знакопеременный ряд (а также ряд с комплексными членами ) называется условно сходящимся, если он сходится, но не сходится абсолютно.

Перечислим основные теоремы для знакопеременных рядов:

Теорема 1.Всякий абсолютно сходящийся ряд сходится.

Теорема 2.Если 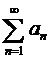- абсолютно сходящийся ряд с суммой s, а сумма ряда 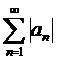равна S, то |s|≤S.

Теорема 3.Если в абсолютно сходящемся ряде произвольным образом переставить члены, то полученный ряд также будет сходиться, а сумма его будет равна сумме исходного ряда.

Признаки сходимости знакопеременных рядов.

Признак Абеля.

Пусть дан ряд 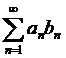. Если последовательность 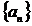монотонна и ограничена, а ряд 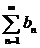сходится, то ряд 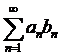сходится.

Признак Дирихле.

Пусть дан ряд 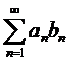. Если последовательность 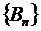, 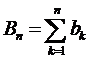ограничена, а последовательность 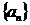монотонно стремится к нулю, то ряд 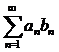сходится.

Определение.Знакопеременный ряд называется знакочередующимся, если соседние его члены имеют различные знаки, то есть ряд вида .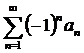

Признак Лейбница (для знакочередующихся рядов).

Если последовательность 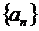положительных чисел монотонно стремится к нулю, то ряд 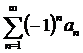сходится и его остаток 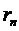удовлетворяет неравенству .

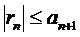Обратим внимание на то, что в признаке сходимости Лейбница указываются триусловия, которым должен удовлетворять ряд: знакочередуемость членов ряда, а также монотонность и сходимость к нулю их абсолютных величин. Убедимся в том, что каждое из этих трёх условий является существенным.

Пример 23.

В ряде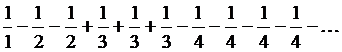

Абсолютные величины членов не возрастают и стремятся к нулю, однако, все частичные суммы вида

,

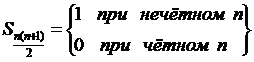а остальные принимают промежуточные значения. Очевидно, такая последовательность частичных сумм предела не имеет, и потому ряд расходится.

Пример 24.

Ряд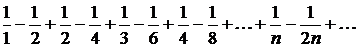

знакочередующийся, но нет монотонного стремления членов ряда к нулю. Этот ряд расходится. В самом деле, если бы он сходился, то в том числе и по ассоциативному закону:

Если в сходящемся ряде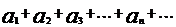

произвольно объединить соседние члены в группы, не нарушая порядка членов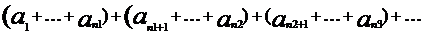

то составленный из этих групп ряд будет сходиться и иметь ту же сумму, что и первоначальный ряд.

Но ряд

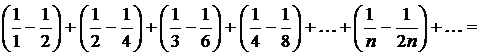
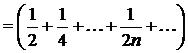
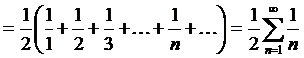
является гармоническим, который, как известно, расходится.

Наконец, невыполнение третьего условия признака Лейбница - стремления к нулю абсолютного значения члена ряда при n→∞ - это нарушение необходимого признака сходимости ряда.

В заключение приведём несколько примеров:

Пример 25.

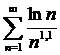
Данный ряд не является знакопеременным, но для исследования его на сходимость хорошо подходит признак Абеля.

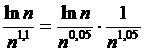
Последовательность 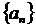= 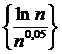является ограниченной и монотонной,

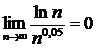,что доказывают по правилу Лопиталя (0,05>0), ряд 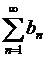=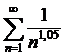сходится, как ряд Дирихле для p=1,05>1. Следовательно, ряд 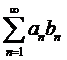=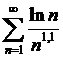сходится.

Пример 26.

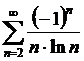
Данный ряд - знакочередующийся, или ряд Лейбница. Начинаем с исследования на абсолютную сходимость:

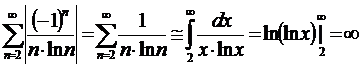ряд из модулей расходится по интегральному признаку - абсолютной сходимости нет.

Применим признак Лейбница:

Последовательность 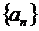= 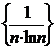монотонно стремится к нулю, следовательно, ряд 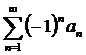=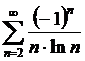сходится условно.