Знакопостоянные ряды, ряды с положительными членами

Установление сходимости или расходимости числового ряда −
основной вопрос теории рядов; нахождение суммы ряда в случае его сходимости – второстепенная задача. Вопрос сходимости проще всего решается для знакопостоянных рядов, когда все члены ряда одного знака. Для определённости будем рассматривать ряды с положительными ( 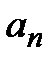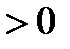) или с неотрицательными членами (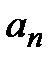 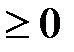). Характерным свойством таких рядов является монотонное возрастание (не убывание) последовательности частичных сумм:

.

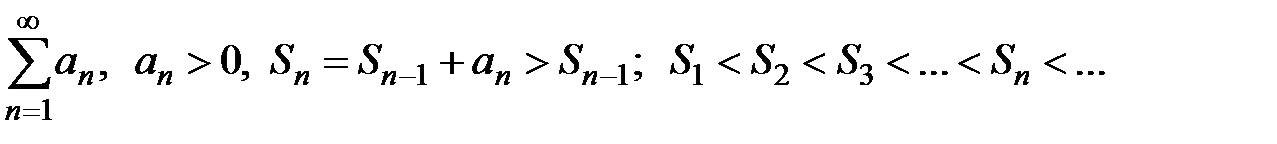Ряд с положительными членами всегда имеет сумму; если эта сумма конечна, то ряд сходится.

Выяснение сходимости рядов с положительными членами опирается на признаки сходимости, которые являются либо необходимыми, либо достаточными, либо необходимыми и достаточными. В частности, к таким рядам применим приведенный выше необходимый признак сходимости рядов (теорема 1). Существует признак, являющийся необходимым и достаточным, который устанавливается следующей теоремой.

Теорема 2. Для сходимости ряда с положительными членами необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена сверху.

Доказательство (необходимость). Пусть ряд сходится, тогда последовательность его частичных сумм сходится, а значит, она ограничена сверху.

Доказательство (достаточность). Так как последовательность частичных сумм монотонно возрастает и ограничена сверху, то она имеет предел, т.е.соответствующий ряд сходится (теорема Вейерштрасса для числовых

последовательностей). Теорема доказана.

Следует отметить, что на практике этот признак трудно применим, хотя и представляет собой большой теоретический интерес.

Далее рассматриваются некоторые признаки сходимости рядов с положительными членами, удобные для практического применения, которые являются только достаточными признаками (интегральный и радикальный признаки Коши, признаки сравнения, признак Даламбера).

1.5. Интегральный признак Коши сходимости ряда
с положительными членами

Теорема 3 (интегральный признак Коши). Пусть дан ряд 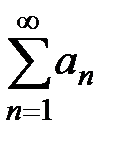, члены которого удовлетворяют трём условиям:

а) 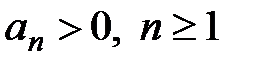, т.е. исходный ряд с положительными членами;

б) члены ряда монотонно убывают, т.е. ;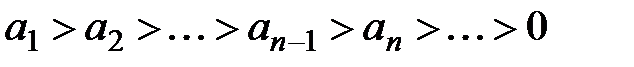

в) общий член ряда стремится к нулю: .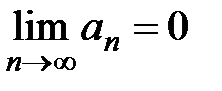

Пусть существует непрерывная, монотонно убывающая, определённая при 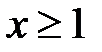функция f(x), такая что 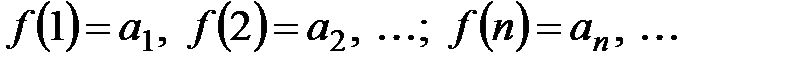, т.е. 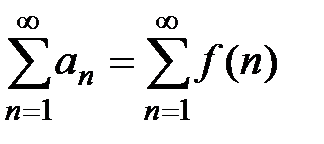. Тогда, если несобственный интеграл 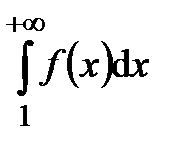сходится, то ряд 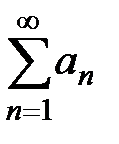тоже сходится; если указанный интеграл расходится, то этот ряд расходится.

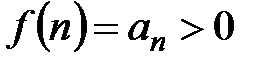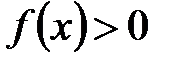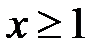Доказательство. Из условий теоремы следует при . Рассмотрим криволинейную трапецию, ограниченную линиями 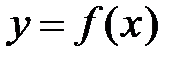, , 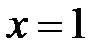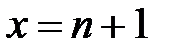и осью 0х (рис.1). Разобьём отрезок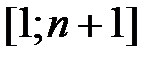

точками 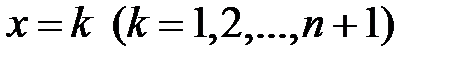и рассмотрим n криволинейных трапеций.

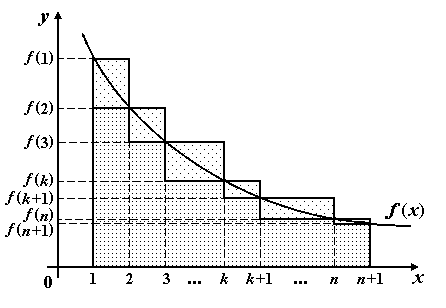
Рис. 1. Площадь криволинейной трапеции

Из геометрического смысла интеграла площадь криволинейной

трапеции 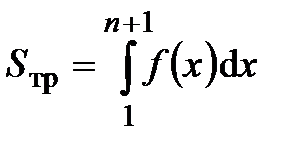. Заменим эту площадь суммой площадей n

прямоугольников с единичными основаниями:

, ,

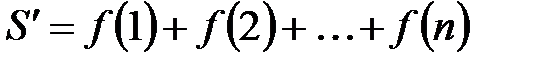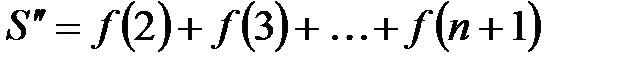причём 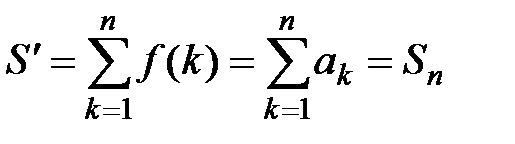, а .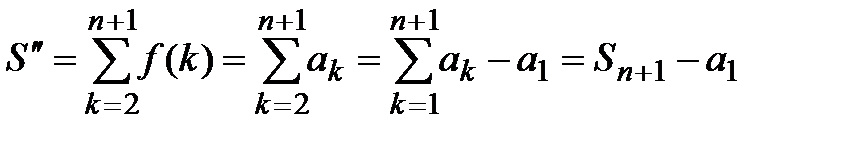

Из графика (рис. 1) следует: 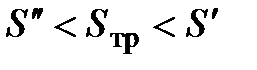, т.е. .

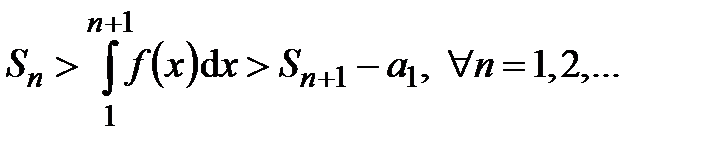Рассмотрим два случая.

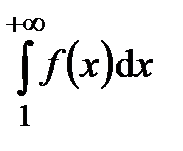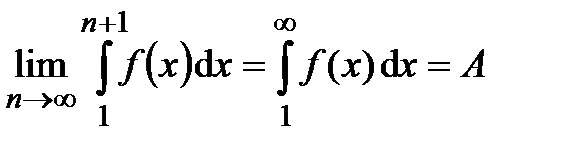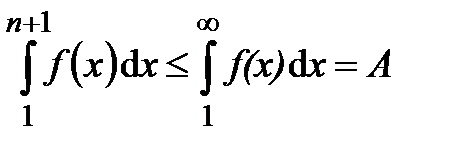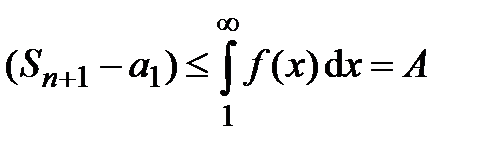1) Пусть сходится, т.е. имеет конечный предел . Так как , то и .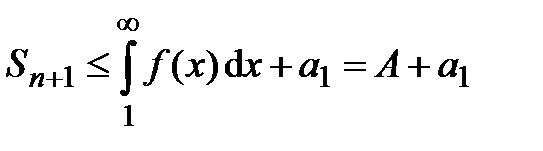

Итак, частичные суммы ряда ограничены 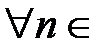N, тогда по теореме 2

(необходимый и достаточный признак сходимости ряда с положительными членами) ряд 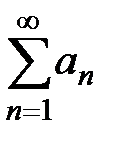сходится, значит, существует .

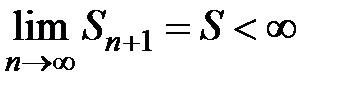2) Пусть интеграл 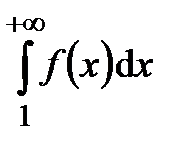расходится, т.е. 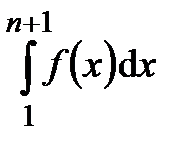неограниченно возрастает при 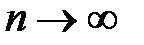. Тогда из неравенства 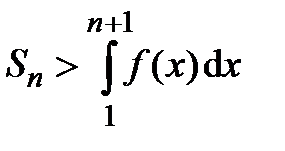следует, что последовательность 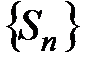неограниченно возрастает: 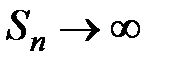, т.е. ряд расходится. Теорема доказана.

Замечание 1. Теорема остаётся верной и тогда, когда её условия выполняются не для всех членов ряда, а лишь начиная с k-го ( 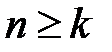), в таком случае рассматривается интеграл .
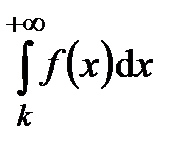Замечание 2. Интегральный признак Коши существенно облегчает исследование сходимости ряда, так как позволяет свести этот вопрос к выяснению сходимости интеграла от удачно подобранной соответствующей функции 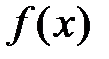, что легко выполняется, применяя методы интегрального исчисления.