Ряды с членами произвольного знака. Абсолютная и условная сходимость
Рассмотрим распространенный тип числового ряда, так называемые знакочередующиеся ряды, элементы которых имеют чередующиеся знаки. Полагая первый член положительным, знакопеременный ряд можно записать в виде
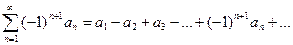 | (9.4.1) |
где 
.
Для знакопеременных рядов имеет место достаточный признак сходимости.
Теорема (признак Лейбница)
Если члены знакочередующегося ряда (9.4.1), будучи взяты по модулю, образуют не возрастающую бесконечно малую последовательность, т.е.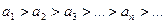 
и 
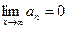, то этот ряд сходится.
Приведем примеры знакочередующихся рядов.
Пример
Исследовать сходимость ряда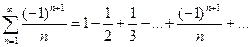 
.
Решение
Этот ряд сходится по признаку Лейбница, так как его члены убывают по абсолютной величине 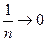и 
при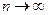 
.
Пример
Исследовать сходимость ряда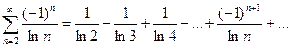 
.
Решение
Нетрудно убедиться, что данный ряд удовлетворяет условиям Теоремы 1 и потому сходится.
Пример
Исследовать сходимость ряда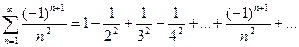 
.
Решение
Так как члены знакочередующегося ряда убывают по абсолютной величине и предел общего члена ряда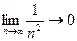 
, то по признаку Лейбница ряд сходится.
Замечание
В теореме Лейбница существенно не только условие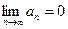 
, но и условие 
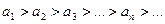. Так, например, для ряда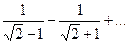 
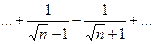второе условие нарушено и, хотя 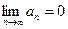, ряд расходится. Это видно, если данный ряд представить в виде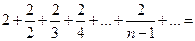 
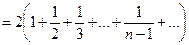, т.е. удвоенного гармонического ряда.
Определение
Под знакопеременным рядом будем понимать ряд, в котором любой его член может быть как положительным, так и отрицательным.
Рассмотрим случай ряда с членами, имеющими произвольные знаки:
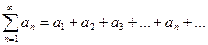 | (9.4.2) |
Одновременно рассмотрим ряд
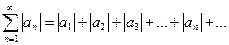 | (9.4.3) |
где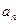 
– члены ряда (9.4.2).
Теорема (достаточный признак сходимости знакопеременного ряда)
Из сходимости ряда (9.4.3) следует сходимость ряда (9.4.2).
Определение
Ряд называется абсолютно сходящимся, если сходится как сам ряд, так и ряд, составленный из абсолютных величин его членов.
Определение
Ряд называется условно сходящимся,если сам ряд сходится, а ряд, составленный абсолютных величин его членов, расходится.
Приведем примерыабсолютной и условной сходимости числовых рядов.
Пример
Ряд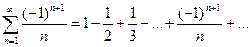 
сходится по признаку Лейбница, однако гармонический ряд 
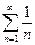расходится, следовательно, сходимость условного ряда является условной.
Пример
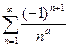, a>0. При a>1 этот ряд сходится абсолютно (как обобщенный гармонический ряд). При 
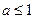данный ряд сходится условно.
Грубо говоря, различие между абсолютно сходящимися и условно сходящимися рядами заключается в следующем: абсолютно сходящиеся ряды сходятся в основном в силу того, что их члены быстро убывают, а условно сходящиеся ряды – в результате того, что положительные и отрицательные слагаемые уничтожают друг друга.
Свойства абсолютно и условно сходящихся рядов существенно отличаются. Абсолютно сходящиеся ряды по своим свойствам напоминают конечные суммы, их можно складывать, перемножать, переставлять местами члены ряда.
Условно сходящиеся ряды такими свойствами не обладают. Возьмем, например, ряд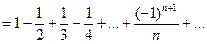 
. Переставим члены местами и сгруппируем их следующим образом: 
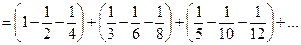. Перепишем ряд в виде: 
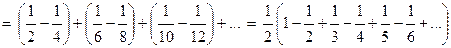, т.е. от перестановки членов ряда сумма его уменьшилась в два раза.
Можно показать (Теорема Римана), что от перестановки членов условно сходящегося ряда можно получить ряд, имеющий любую наперед заданную сумму, и даже расходящийся ряд.
В заключение приведем без доказательства один важный признак сходимости числового ряда.
Теорема (признак Дирихле –Абеля)
Пусть дан ряд
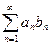 . | (9.4.4) |
Если последовательность частичных сумм ряда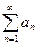 
ограничена и последовательность 
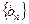является не возрастающей и бесконечно малой, то ряд (9.4.4) сходится.
Заметим, что признак Лейбница является частным случаем этой теоремы при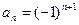 
.
Пример
Применим сформулированный выше признак Дирихле–Абеля к установлению сходимости ряда
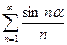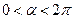 ,  . | (9.4.5) |
Решение
Положим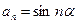 
, 
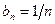. Вычислим частичные суммы ряда 
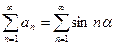. Для этого умножим и поделим каждое слагаемое этой суммы на постоянную величину 
:
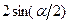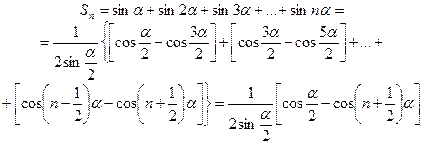
Таким образом, частичные суммы ряда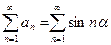 
ограничены, а последовательность 
является не возрастающей и бесконечно малой; условия Дирихле–Абеля выполняются, т.е. ряд (9.4.5) сходится.