Знакочередующиеся ряды. Теорема Лейбница

Теорема 8.7.Если члены знакочередующегося ряда 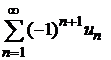монотонно убывают 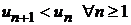и стремятся к нулю 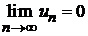, то ряд сходится; причем сумма ряда по абсолютной величине не превосходит первого члена ряда .

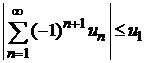Д о к а з а т е л ь с т в о. По определению знакочередующегося ряда

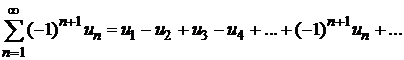
предполагается, что члены ряда положительные .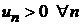

Рассмотрим две частичные суммы ряда: с четным числом членов ряда 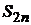и с нечетным числом членов .

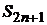В сумме с четным числом членов 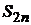сначала сгруппируем члены попарно следующим образом

.

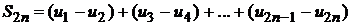Так как члены ряда монотонно убывают ( 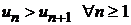), то разность в каждой скобке суммы 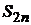больше нуля и эта сумма монотонно возрастает с увеличением числа членов 2n.

Теперь сгруппируем члены этой суммы следующим образом

.

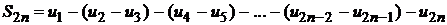Так как в этой сумме также разность в каждой скобке больше нуля, то сумма монотонно убывает с увеличением числа членов 2n и не превосходит первого члена ряда .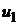

Следовательно, последовательность частичных сумм ряда с четным числом членов монотонно возрастает и ограничена. Поэтому по теореме Вейерштрасса она имеет некоторый предел .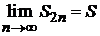

Найдем также предел частичных сумм ряда с нечетным числом членов.

.

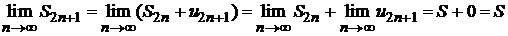При нечетном числе членов ряда сумма 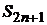также не превосходит первого члена ряда .

.

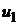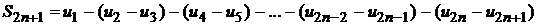Таким образом, предел частичных сумм знакочередующегося ряда существует, т. е. ряд всегда сходится, если его члены монотонно убывают и стремятся к нулю.

Частичные суммы знакочередующегося ряда меньше первого члена ряда

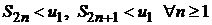. Члены ряда стремятся к нулю 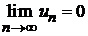, поэтому сумма ряда не может превосходить первого члена ряда .

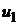Пример 8.17. Исследовать сходимость ряда .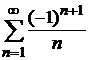

Члены ряда монотонно убывают 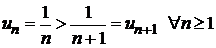и стремятся к нулю . Следовательно, ряд сходится.

Пример 8.18. Исследовать сходимость ряда .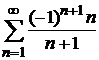

Предел членов ряда при неограниченном возрастании их номеров отличен от нуля . По следствию необходимого признака сходимости числовых рядов рассматриваемый ряд расходится.

Знакопеременные ряды. Теорема об абсолютной сходимости

Числового ряда

Теорема 8.8.Числовой ряд 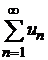сходится, если сходится ряд, составленный из абсолютных величин его членов .

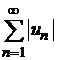Д о к а з а т е л ь с т в о. Пусть ряд 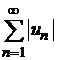сходится. Тогда по свойству 1 сходящихся рядов также сходится ряд .

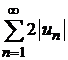Так как 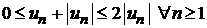, то по первому признаку сравнения рядов (теорема 8.2) также сходится ряд 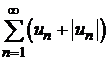. На основании свойства 2 сходящихся рядов сходится разность двух рядов

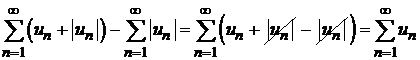, т. е. исходный ряд.

Ряд называется абсолютно сходящимся, если он сходится и сходится ряд, составленный из абсолютных величин его членов.

Ряд называется условно сходящимся, если он сходится, а ряд, составленный из абсолютных величин его членов, расходится.

Пример 8.19. Исследовать сходимость ряда .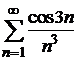

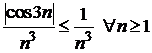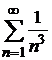Так как и ряд сходится как обобщенно гармонический ряд 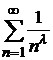при 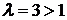, то по теореме 8.2 сравнения рядов сходится ряд 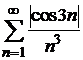, а по теореме об абсолютной сходимости сходится также ряд 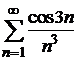. Следовательно, исходный ряд сходится; причем абсолютно.

Пример 8.20. Исследовать на абсолютную сходимость ряд .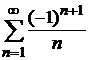

Ранее было показано, что данный знакочередующийся ряд сходится (пример 8.15). Ряд, составленный из абсолютных величин данного ряда, является гармоническим, который, как известно, расходится. Это означает, что исходный ряд сходится условно.

Глава 9. Степенные ряды