Знакопеременные и знакочередующиеся ряды
6. Ряд 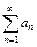 с членами, имеющими разные знаки, называется знакопеременным. Если в знакопеременном ряде
с членами, имеющими разные знаки, называется знакопеременным. Если в знакопеременном ряде 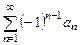 , где
, где 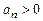 (т.е. знаки чередуются), то ряд называется знакочередующимся.
(т.е. знаки чередуются), то ряд называется знакочередующимся.
7. Признак Лейбница. Пусть дан знакочередующийся ряд 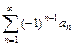 , где an > 0. Если 1) члены знакочередующегося ряда убывают по абсолютной величине
, где an > 0. Если 1) члены знакочередующегося ряда убывают по абсолютной величине 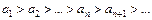 и 2) предел его общего члена при
и 2) предел его общего члена при 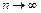 равен нулю, т. е.
равен нулю, т. е. 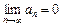 , то исходный ряд сходится, а его сумма не превосходит первого члена
, то исходный ряд сходится, а его сумма не превосходит первого члена 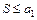 .
.
8. Пусть дан знакопеременный ряд 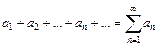 . Если соответствующий ряд
. Если соответствующий ряд 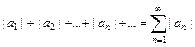 сходится, то данный ряд сходится абсолютно.
сходится, то данный ряд сходится абсолютно.
9. Если знакопеременный ряд 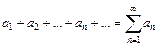 сходится по признаку Лейбница, а соответствующий ряд
сходится по признаку Лейбница, а соответствующий ряд 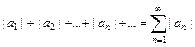 расходится, то данный ряд сходится условно.
расходится, то данный ряд сходится условно.
10. Сумма 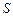 сходящегося по признаку Лейбница ряда можно представить как
сходящегося по признаку Лейбница ряда можно представить как 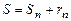 , где
, где 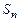 - сумма первых
- сумма первых 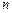 членов ряда, а
членов ряда, а 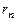 - сумма остатка ряда (который представляет собой знакочередующийся ряд, удовлетворяющий условиям признака Лейбница, первый член которого
- сумма остатка ряда (который представляет собой знакочередующийся ряд, удовлетворяющий условиям признака Лейбница, первый член которого 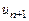 , и, следовательно, для него
, и, следовательно, для него 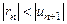 ). Отсюда следует вывод: погрешность при приближенном вычислении суммы сходящегося знакочередующегося ряда, удовлетворяющего условиям признака Лейбница, по абсолютной величине не превышает абсолютной величины первого отброшенного члена.
). Отсюда следует вывод: погрешность при приближенном вычислении суммы сходящегося знакочередующегося ряда, удовлетворяющего условиям признака Лейбница, по абсолютной величине не превышает абсолютной величины первого отброшенного члена.
Функциональные ряды
Основные понятия
11. Ряд 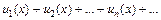 , членами которого являются функции, называется функциональным.
, членами которого являются функции, называется функциональным.
12. Областью абсолютной сходимости данного функционального ряда называется множество значений х, при которых данный ряд сходиться как числовой ряд.
13. Область абсолютной сходимости функционального ряда находится из неравенства 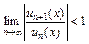 .
.
14. Степенным рядом называется ряд вида 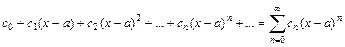 .
.
15. Радиус абсолютной сходимости степенного ряда: 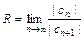 или
или 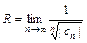 .
.
16. Интервалом абсолютной сходимости степенного ряда называется интервал вида (a – R; a + R).
17. Интервал абсолютной сходимости с исследованными границами называется областью абсолютной сходимости степенного ряда.
18. Теорема Абеля: 1) если степенной ряд сходится при значении 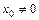 , то он сходится и притом абсолютно при всех значениях х таких, что |x| < |x0|; 2) если степенной ряд расходится при х1, то он расходится при всех значениях х таких, что |x| > |x1|.
, то он сходится и притом абсолютно при всех значениях х таких, что |x| < |x0|; 2) если степенной ряд расходится при х1, то он расходится при всех значениях х таких, что |x| > |x1|.
19. Основные свойства степенных рядов в интервале (a – R; a + R) абсолютной сходимости:
1) В интервале (a – R; a + R) сумма ряда есть непрерывная функция.
2) Степенной ряд в каждой точке интервала (a – R; a + R) можно почленно дифференцировать бесконечное число раз.
3) Степенной ряд можно почленно интегрировать по любому интервалу 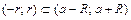 .
.
20. Ряд Тейлора для функции 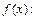
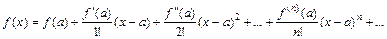
21. Частный случай ряда Тейлора для функции 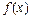 при а = 0 – ряд Маклорена:
при а = 0 – ряд Маклорена: 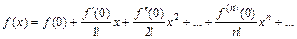
22. Разложение основных функций в ряд Маклорена:
| Разложение | Область абс. сход. |
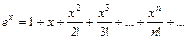 | 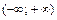 |
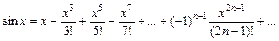 | 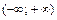 |
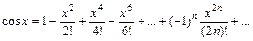 | 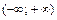 |
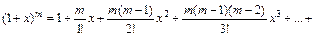 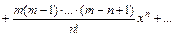 | 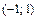 |
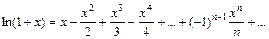 | 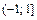 |
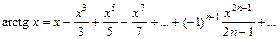 | 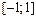 |
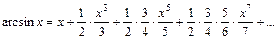 |  |
23. Рассмотрим два способа решения дифференциальных уравнений при помощи рядов: а) применение ряда Тейлора и б) способ неопределенных коэффициентов.
а) Применение ряда Тейлора. Пусть требуется найти решение уравнения
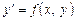 ,
,
удовлетворяющее начальному условию 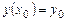 . Представим решение уравнения в виде суммы ряда Тейлора
. Представим решение уравнения в виде суммы ряда Тейлора
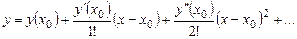 .
.
Из начального условия известно 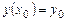 . Тогда из уравнения
. Тогда из уравнения 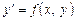 найдем
найдем 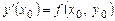 . Далее, дифференцируя
. Далее, дифференцируя 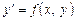 , получим
, получим
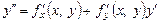 ,
,
откуда находим 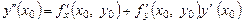 . Аналогично этому, снова дифференцируя и полагая
. Аналогично этому, снова дифференцируя и полагая 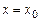 , найдем
, найдем 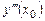 , и так далее. В результате можно найти сколь угодно много членов разложения
, и так далее. В результате можно найти сколь угодно много членов разложения 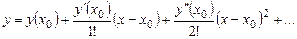 .
.
б) Способ неопределенных коэффициентов. Этот способ особенно удобен при решении линейных уравнений. Он состоит в следующем: искомое решение 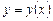 представляется рядом
представляется рядом 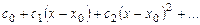 с буквенными коэффициентами
с буквенными коэффициентами 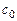 ,
, 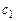 ,
, 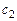 ,… . Подставляя этот ряд в уравнение и приравнивая коэффициенты при одинаковых степенях разности
,… . Подставляя этот ряд в уравнение и приравнивая коэффициенты при одинаковых степенях разности 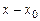 , находят
, находят 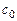 ,
, 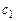 ,
, 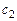 ,… .
,… .
24. Тригонометрическим называется функциональный ряд вида 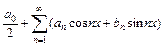 .
.
25. Ряд Фурье для функции 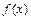 периода 2p:
периода 2p: 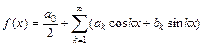 , где
, где 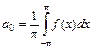 ,
, 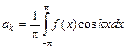 и
и 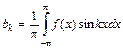 .
.
26. Если 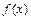 – четная функция периода 2p, то ряд Фурье имеет вид
– четная функция периода 2p, то ряд Фурье имеет вид 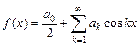 , где
, где 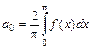 ,
, 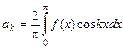 и
и 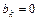 .
.
27. Если 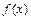 – нечетная функция периода 2p, то ряд Фурье имеет вид
– нечетная функция периода 2p, то ряд Фурье имеет вид 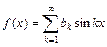 , где
, где 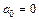 ,
, 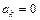 и
и 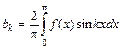 .
.
28. Условия Дирихле. Функция 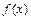 на
на 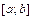 ограничена и
ограничена и 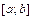 можно разбить на некоторое число отрезков, на каждом из которых
можно разбить на некоторое число отрезков, на каждом из которых 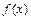 была бы непрерывна и изменялась монотонно.
была бы непрерывна и изменялась монотонно.
29. Ряд Фурье для функции 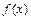 , заданной на промежутке
, заданной на промежутке 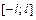 :
: 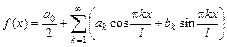 , где
, где 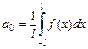 ,
, 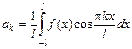 и
и 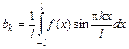 .
.
30. Если 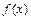 – четная функция, заданная на промежутке
– четная функция, заданная на промежутке 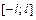 , то ряд Фурье имеет вид
, то ряд Фурье имеет вид 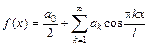 , где
, где 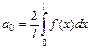 ,
, 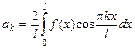 и
и 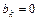 .
.
31. Если 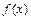 – нечетная функция, заданная на промежутке
– нечетная функция, заданная на промежутке 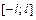 , то ряд Фурье имеет вид
, то ряд Фурье имеет вид 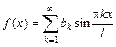 , где
, где 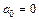 ,
, 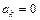 и
и 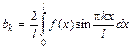 .
.
4.2. Контрольные задания
1. Найти общее решение линейного дифференциального уравнения и частное решение, удовлетворяющее начальному условию y(x0) = y0.
1. 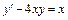 ,
, 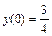 . 2.
. 2. 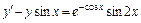 ,
, 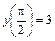 .
.
3. 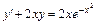 , y(0) = 5. 4.
, y(0) = 5. 4. 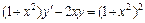 , y(–2) = 5.
, y(–2) = 5.
5. 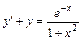 , y(0) = 2. 6.
, y(0) = 2. 6. 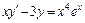 , y(1) = e.
, y(1) = e.
7. 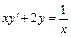 , y(3) = 1. 8.
, y(3) = 1. 8. 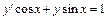 , y(0) = 2.
, y(0) = 2.
9. 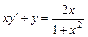 , y(1) = 0. 10.
, y(1) = 0. 10. 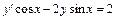 , y(0) = 3.
, y(0) = 3.
2. Найти общее решение линейного неоднородного дифференциального уравнения 2-го порядка с постоянными коэффициентами с правой частью специального вида и частное решение, удовлетворяющее начальным условиям y(x0) = y0 и 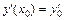
1. 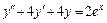 , y(0) = –2,
, y(0) = –2, 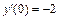 .
.
2. 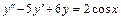 , y(0) = 3,
, y(0) = 3, 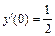 .
.
3. 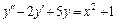 , y(0) = –3,
, y(0) = –3, 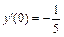 .
.
4. 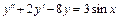 , y(0) = –1,
, y(0) = –1, 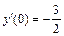 .
.
5. 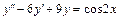 , y(0) = 1,
, y(0) = 1, 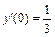 .
.
6. 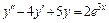 , y(0) = 2,
, y(0) = 2, 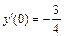 .
.
7. 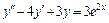 , y(0) = 2,
, y(0) = 2, 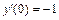 .
.
8. 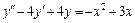 , y(0) = 3,
, y(0) = 3, 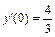 .
.
9. 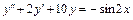 , y(0) = 0,
, y(0) = 0, 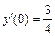 .
.
10. 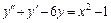 , y(0) = 0,
, y(0) = 0, 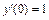 .
.
3. Найти общее решение системы уравнений
1. 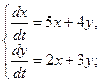 2.
2. 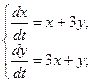
3. 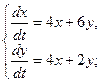 4.
4. 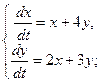
5. 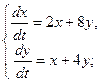 6.
6. 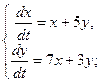
7. 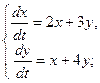 8.
8. 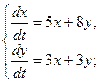
9. 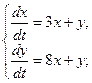 10.
10. 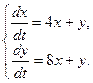
4. Написать три первых члена степенного ряда, найти его область абсолютной сходимости.
1. 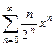 . 2.
. 2. 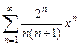 . 3.
. 3. 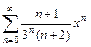 .
.
4. 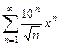 . 5.
. 5. 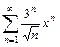 . 6.
. 6. 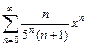 .
.
7. 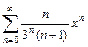 . 8.
. 8. 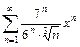 . 9.
. 9. 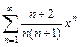 .
.
10. 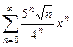 .
.
5. Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в степенной ряд.
1. 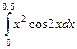 . 2.
. 2. 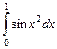 . 3.
. 3. 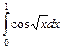 .
.
4. 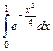 . 5.
. 5. 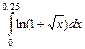 . 6.
. 6. 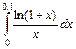 .
.
7. 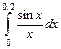 . 8.
. 8. 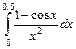 . 9.
. 9. 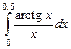 .
.
10. 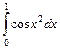 .
.
6. Найти три первых отличных от нуля члена разложения в степенной ряд решения 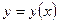 дифференциального уравнения
дифференциального уравнения 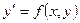 , удовлетворяющего начальному условию
, удовлетворяющего начальному условию 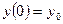 .
.
1. 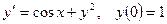 ; 2.
; 2. 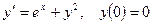 ;
;
3. 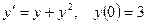 ; 4.
; 4. 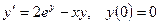 ;
;
5. 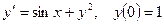 ; 6.
; 6. 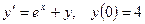 ;
;
7. 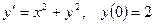 ; 8.
; 8. 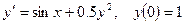 ;
;
9. 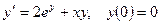 ; 10.
; 10. 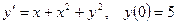 .
.
7. Разложить данную функцию 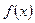 в ряд Фурье в интервале
в ряд Фурье в интервале 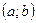 .
.
1. 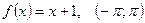 ; 2.
; 2. 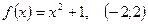 ;
;
3. 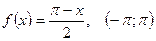 ; 4.
; 4. 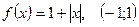 ;
;
5. 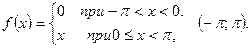 ;6.
;6. 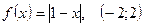 ;
;
7. 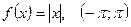 ; 8.
; 8. 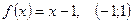 ;
;
9. 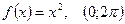 ; 10.
; 10. 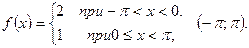
4.3. Пример решения контрольной работы
Задание 1. Найти общее решение линейного дифференциального уравнения первого порядка 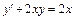 и частное решение, удовлетворяющее начальному условию y(0) = 0.
и частное решение, удовлетворяющее начальному условию y(0) = 0.
Решение. Общее решение будем искать методом Бернулли: 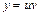 , где
, где 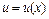 ,
, 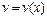 – две новые неизвестные функции, тогда
– две новые неизвестные функции, тогда 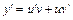 . Подставляя в исходное уравнение, получаем
. Подставляя в исходное уравнение, получаем 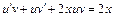 или
или 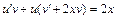 . Подберем функцию v так, чтобы выражение в скобках было равно нулю, тогда получим
. Подберем функцию v так, чтобы выражение в скобках было равно нулю, тогда получим 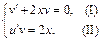 Найдем частное решение уравнения (I) при С1 = 0, которое является ДУ с разделяющимися переменными. Для этого в этом уравнении разделим переменные x и y:
Найдем частное решение уравнения (I) при С1 = 0, которое является ДУ с разделяющимися переменными. Для этого в этом уравнении разделим переменные x и y: 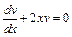 или
или 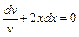 . Проинтегрировав обе части, получим
. Проинтегрировав обе части, получим 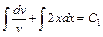 или
или 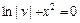 (при С1= 0) или
(при С1= 0) или 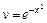 – частное решение уравнения (I). Подставляя полученную функцию v в уравнение (II), получаем тоже ДУ с разделяющимися переменными:
– частное решение уравнения (I). Подставляя полученную функцию v в уравнение (II), получаем тоже ДУ с разделяющимися переменными: 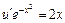 , для которого найдем его общее решение. Разделяем переменные:
, для которого найдем его общее решение. Разделяем переменные: 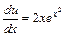 или
или 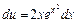 . Интегрируем обе части:
. Интегрируем обе части: 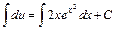 или
или 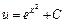 – общее решение уравнения
– общее решение уравнения 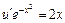 . Таким образом
. Таким образом 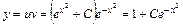 – общее решение исходного уравнения.
– общее решение исходного уравнения.
Для нахождения частного решения исходного уравнения, удовлетворяющего начальному условию y(0) = 0 подставим в найденное общее решение x = 0 и y = 0 и найдем постоянную С: 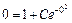 или
или 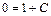 , т. е. С = –1. Таким образом,
, т. е. С = –1. Таким образом, 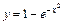 – частное решение исходного уравнения при y(0) = 0.
– частное решение исходного уравнения при y(0) = 0.
Ответ: 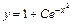 – общее решение;
– общее решение; 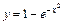 – частное решение.
– частное решение.
Задание 2. Найти общее решение линейного неоднородного дифференциального уравнения 2-го порядка с постоянными коэффициентами с правой частью специального вида и частное решение, удовлетворяющее начальным условиям y(x0) = y0 и 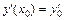
1) 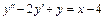 , y(0) = –1,
, y(0) = –1, 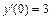 ;
;
2) 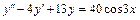 , y(0) = 1,
, y(0) = 1, 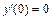 ;
;
3) 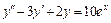 , y(0) = 2,
, y(0) = 2, 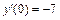 .
.
Решение. Общее решение линейного неоднородного дифференциального уравнения 2-го порядка с постоянными коэффициентами с правой частью специального вида будем искать в виде 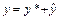 , где
, где 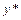 – общее решение соответствующего линейного однородного ДУ 2-го порядка с постоянными коэффициентами, а
– общее решение соответствующего линейного однородного ДУ 2-го порядка с постоянными коэффициентами, а 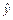 – некоторое частное решение исходного уравнения.
– некоторое частное решение исходного уравнения.
1) Найдем общее решение 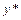 соответствующего линейного однородного ДУ 2-го порядка с постоянными коэффициентами
соответствующего линейного однородного ДУ 2-го порядка с постоянными коэффициентами 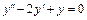 . Характеристическое уравнение
. Характеристическое уравнение 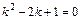 имеет два равных корня
имеет два равных корня 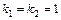 , значит
, значит 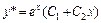 .
.
Найдем частное решение 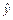 исходного уравнения. В нем правая часть
исходного уравнения. В нем правая часть 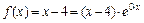 есть формула вида
есть формула вида 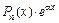 , причем n = 1 и a = 0 – не корень характеристического уравнения. Поэтому частное решение
, причем n = 1 и a = 0 – не корень характеристического уравнения. Поэтому частное решение 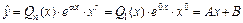 , где А и В – неопределенные коэффициенты. Тогда
, где А и В – неопределенные коэффициенты. Тогда 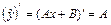 и
и 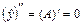 . Подставив
. Подставив 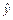 ,
, 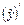 ,
, 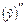 в исходное уравнение, получим –2А + Ax + B = x – 4 или Ax + (–2А + B) = x – 4. Приравнивая коэффициенты при одинаковых степенях x, получаем систему уравнений
в исходное уравнение, получим –2А + Ax + B = x – 4 или Ax + (–2А + B) = x – 4. Приравнивая коэффициенты при одинаковых степенях x, получаем систему уравнений 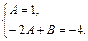 Отсюда A = 1, B = –2. Поэтому частное решение исходного уравнения имеет вид
Отсюда A = 1, B = –2. Поэтому частное решение исходного уравнения имеет вид 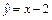 . Следовательно,
. Следовательно, 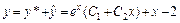 – общее решение исходного уравнения.
– общее решение исходного уравнения.
Для нахождения частного решения исходного уравнения, удовлетворяющего начальным условиям y(0) = –1, 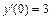 найдем
найдем 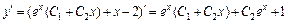 . Подставим начальные условия в найденное общее решение и его производную, получим систему
. Подставим начальные условия в найденное общее решение и его производную, получим систему 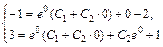 или
или 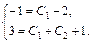 Отсюда С1 = С2 = 1. Таким образом, искомое частное решение имеет вид:
Отсюда С1 = С2 = 1. Таким образом, искомое частное решение имеет вид: 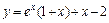 .
.
2) Найдем общее решение 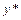 соответствующего однородного уравнения
соответствующего однородного уравнения 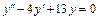 . Составим характеристическое уравнение
. Составим характеристическое уравнение 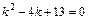 , дискриминант
, дискриминант 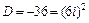 , имеет два комплексных корня
, имеет два комплексных корня 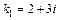 ,
, 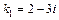 . Следовательно,
. Следовательно, 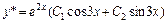 .
.
Найдем частное решение 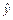 исходного уравнения. Его правая часть
исходного уравнения. Его правая часть 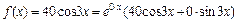 есть формула вида
есть формула вида 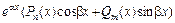 , причем n = m = 0, a = 0, b = 3. Так как числа
, причем n = m = 0, a = 0, b = 3. Так как числа 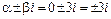 – не корни характеристического уравнения (r = 0), то частное решение имеет вид:
– не корни характеристического уравнения (r = 0), то частное решение имеет вид: 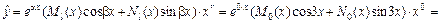
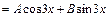 , где А и В – неопределенные коэффициенты,
, где А и В – неопределенные коэффициенты, 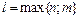 . Найдем
. Найдем 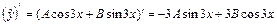 и
и 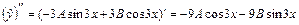 . Подставив
. Подставив 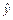 ,
, 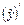 ,
, 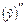 в исходное уравнение, получим
в исходное уравнение, получим 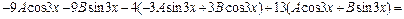
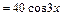 или
или 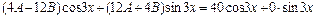 . Приравнивая коэффициенты при синусе и косинусе в обеих частях, получаем систему уравнений
. Приравнивая коэффициенты при синусе и косинусе в обеих частях, получаем систему уравнений 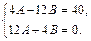 Отсюда A = 1, B = –3. Поэтому частное решение исходного уравнения имеет вид
Отсюда A = 1, B = –3. Поэтому частное решение исходного уравнения имеет вид 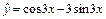 . Следовательно,
. Следовательно, 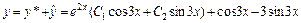 – общее решение исходного уравнения.
– общее решение исходного уравнения.
Для нахождения частного решения исходного уравнения, удовлетворяющего начальным условиям y(0) = 1, 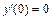 вычислим
вычислим 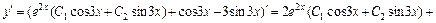
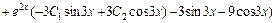 . Подставляя начальные условия в найденное общее решение и его производную, получим систему
. Подставляя начальные условия в найденное общее решение и его производную, получим систему 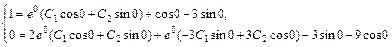 или
или 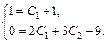 Следовательно, С1 = 0, С2 = 3. Таким образом,
Следовательно, С1 = 0, С2 = 3. Таким образом, 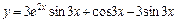 – искомое частное решение.
– искомое частное решение.
3) Найдем общее решение 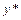 соответствующего однородного уравнения
соответствующего однородного уравнения 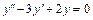 . Характеристическое уравнение
. Характеристическое уравнение 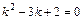 имеет два различных корня
имеет два различных корня 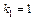 и
и 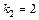 , значит
, значит 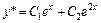 .
.
Найдем частное решение 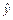 исходного уравнения. В нем правая часть
исходного уравнения. В нем правая часть 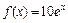 есть формула вида
есть формула вида 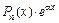 , причем n = 0, а a = 1 – корень характеристического уравнения кратности 1 (r = 1). Поэтому частное решение
, причем n = 0, а a = 1 – корень характеристического уравнения кратности 1 (r = 1). Поэтому частное решение 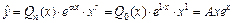 , где А – неопределенный коэффициент. Тогда
, где А – неопределенный коэффициент. Тогда 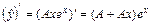 и
и 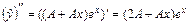 . Подставим
. Подставим 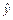 ,
, 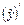 ,
, 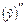 в исходное уравнение и получим
в исходное уравнение и получим 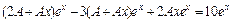 . Сократив оби части равенства на
. Сократив оби части равенства на 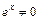 и приведя подобные, получим
и приведя подобные, получим 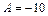 . Поэтому частное решение исходного уравнения имеет вид
. Поэтому частное решение исходного уравнения имеет вид 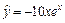 . Следовательно,
. Следовательно, 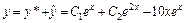 – общее решение исходного уравнения.
– общее решение исходного уравнения.
Для нахождения частного решения исходного уравнения, удовлетворяющего начальным условиям y(0) = 2, 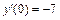 сначала найдем
сначала найдем 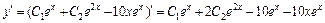 . Подставим начальные условия в найденное общее решение и его производную, получим систему
. Подставим начальные условия в найденное общее решение и его производную, получим систему 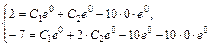 или
или 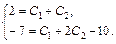 Отсюда С1 = С2 = 1. Итак, частное решение исходного уравнения имеет вид
Отсюда С1 = С2 = 1. Итак, частное решение исходного уравнения имеет вид 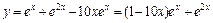 .
.
Ответ: 1) 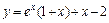 ; 2)
; 2) 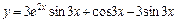 ; 3)
; 3) 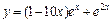 .
.
Задание 3. 1) способ:Найти общее решение системы
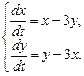
Решение.Перепишем систему в виде
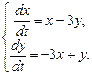
Воспользуемся методом решения при помощи матриц.
Рассмотрим характеристическое уравнение:
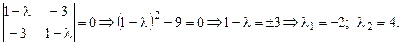
Подставим найденные значения корней характеристического уравнения в систему линейных алгебраических уравнений относительно 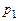 ,
, 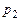 .
.
Для 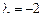 имеем
имеем
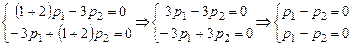 ,
,
(второе уравнение есть следствие первого). Возьмем, например, 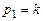 ; тогда
; тогда 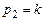 . Полагая
. Полагая 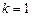 , найдем
, найдем 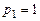 ;
; 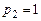 . Итак, для
. Итак, для 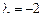 получим
получим 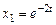 ;
; 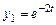 .
.
Для 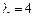 имеем
имеем
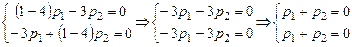 ,
,
(второе уравнение есть следствие первого). Возьмем, например, 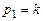 ; тогда
; тогда 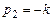 . Полагая
. Полагая 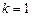 , найдем
, найдем 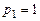 ;
; 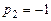 . Итак, для
. Итак, для 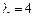 получим
получим 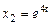 ;
; 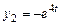 .
.
Фундаментальная система решений:
для 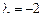 :
: 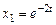 ;
; 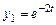 ,
,
для 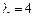 :
: 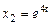 ;
; 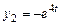 .
.
Следовательно, общее решение системы имеет вид
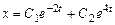 ,
, 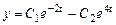 .
.
Ответ: 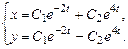 .
.
Задание 3. 2) способ:Решить систему дифференциальных уравнений
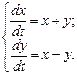
при начальных условиях: 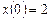 ,
, 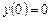 .
.
Решение.Воспользуемся методом исключения. Продифференцируем по 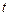 первое уравнение:
первое уравнение:
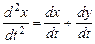 ;
;
исключая из полученного уравнения 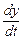 и
и 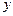 , имеем
, имеем
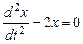 .
.
Корни характеристического уравнения 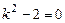 будут
будут 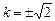 . Следовательно, общее решение для
. Следовательно, общее решение для 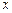 имеет вид
имеет вид
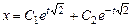 .
.
Общее решение для 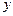 находим из первого уравнения:
находим из первого уравнения:
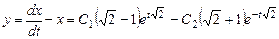 .
.
Воспользуемся начальными условиями для нахождения произвольных постоянных:
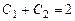 ,
, 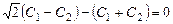 .
.
Отсюда
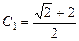 ,
, 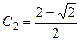 .
.
Таким образом, частное решение имеет вид
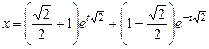 ,
,
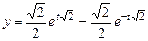 .
.
Ответ: 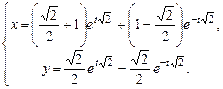
Задание 4. Написать три первых члена степенного ряда 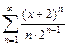 , найти его область абсолютной сходимости.
, найти его область абсолютной сходимости.
Решение. Запишем три первых члена ряда. При n = 1 получаем первый член ряда: 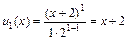 , при n = 2 – второй член:
, при n = 2 – второй член: 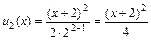 и при n = 3 – третий член ряда:
и при n = 3 – третий член ряда: 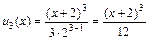 .
.
Для данного ряда имеем а = –2, 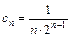 ,
, 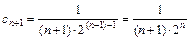 . Найдем радиус сходимости
. Найдем радиус сходимости 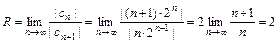 . Тогда интервал абсолютной сходимости ряда по формуле (a – R; a + R) есть (–4; 0).
. Тогда интервал абсолютной сходимости ряда по формуле (a – R; a + R) есть (–4; 0).
Теперь выясним поведение ряда на концах интервала сходимости. При x = –4 получаем числовой знакочередующийся ряд 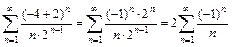 , который сходится согласно признаку Лейбница, т. к. выполняются оба условия признака: 1)
, который сходится согласно признаку Лейбница, т. к. выполняются оба условия признака: 1) 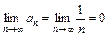 и 2) члены ряда убывают по абсолютной величине
и 2) члены ряда убывают по абсолютной величине 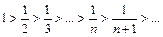 При x = 0 имеем числовой знакоположительный ряд
При x = 0 имеем числовой знакоположительный ряд 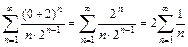 . Это гармонический ряд, который расходится. Таким образом, область абсолютной сходимости исходного ряда имеет вид [–4; 0).
. Это гармонический ряд, который расходится. Таким образом, область абсолютной сходимости исходного ряда имеет вид [–4; 0).
Ответ: 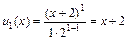 ,
, 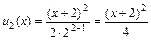 ,
, 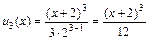 ; [–4; 0).
; [–4; 0).
Задание 5. Вычислить определенный интеграл 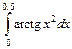 с точностью до 0,001, разложив подынтегральную функцию в степенной ряд.
с точностью до 0,001, разложив подынтегральную функцию в степенной ряд.
Решение. Для разложения подынтегральной функции в степенной ряд воспользуемся формулой 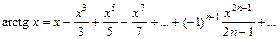 таблицы основных разложений. Заменив в ней x на x2, получим:
таблицы основных разложений. Заменив в ней x на x2, получим:
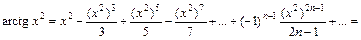
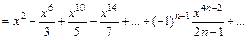
для любого 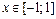 . Так как отрезок интегрирования [0; 0,5] целиком содержится внутри области сходимости ряда, то на основании свойства о почленном интегрировании степенных рядов получим
. Так как отрезок интегрирования [0; 0,5] целиком содержится внутри области сходимости ряда, то на основании свойства о почленном интегрировании степенных рядов получим
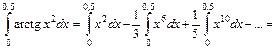
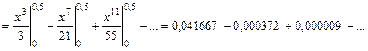
Получили числовой знакочередующийся ряд, удовлетворяющий условиям признака Лейбница: 1) члены знакочередующегося ряда убывают по абсолютной величине: 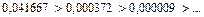 и 2) предел его общего члена при
и 2) предел его общего члена при 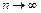 равен нулю:
равен нулю: 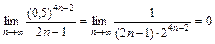 . Так как |a2| = 0,000372 < 0,001, то приближенное значение суммы S полученного ряда будет равно: S » S1 = a1, так как по следствию из признака Лейбница погрешность вычисления r2 = |S – S1| < |a2| < 0,001.
. Так как |a2| = 0,000372 < 0,001, то приближенное значение суммы S полученного ряда будет равно: S » S1 = a1, так как по следствию из признака Лейбница погрешность вычисления r2 = |S – S1| < |a2| < 0,001.
Таким образом, 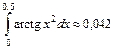 .
.
Ответ: » 0,042.
Задание 6.Найти решение уравнения 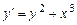 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 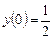 .
.
Решение.а) Применение ряда Тейлора. Так как 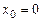 , то представим искомое решение в виде ряда Маклорена
, то представим искомое решение в виде ряда Маклорена
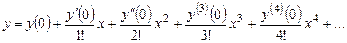 .
.
Из начального условия имеем 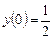 , тогда из уравнения
, тогда из уравнения 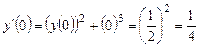 . Дифференцируя уравнение, находим
. Дифференцируя уравнение, находим 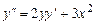 , тогда
, тогда 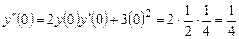 . Снова дифференцируя и подставляя
. Снова дифференцируя и подставляя 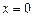 ,
, 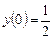 ,
, 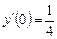 ,
, 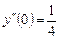 , получаем
, получаем 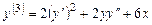 ,
, 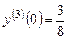 , и так далее. Следовательно, разложение искомой функции имеет вид
, и так далее. Следовательно, разложение искомой функции имеет вид
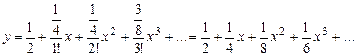 .
.
б) способ неопределенных коэффициентов. Положим, что искомое решение представляется сходящимся степенным рядом
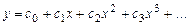 . (1)
. (1)
Используя начальные условия, что 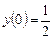 получим
получим 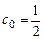 .
.
Дифференцируя ряд (1), получим:
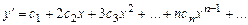 . (2)
. (2)
Подставляя ряды (1) и (2) в данное дифференциальное уравнение, получим:
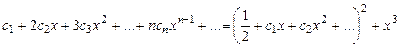 .
.
Приравнивая коэффициенты при одинаковых степенях 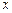 , получим:
, получим:
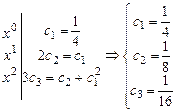
и так далее.
Подставляя найденные коэффициенты в (1), получим решение:
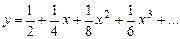 .
.
Ответ: 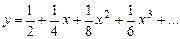 .
.
Задание 7.Разложить в ряд Фурье функцию 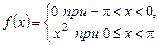 в интервале
в интервале 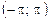 .
.
Решение.Данная функция непрерывна и монотонно возрастает в 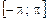 . Следовательно, по теореме Дирихле она разлагается в ряд Фурье в
. Следовательно, по теореме Дирихле она разлагается в ряд Фурье в 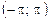 . Найдем ее коэффициенты Фурье по формулам:
. Найдем ее коэффициенты Фурье по формулам:
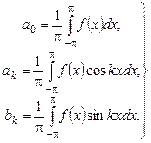
Вследствие того, что функция задана разными формулами на 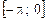 и
и 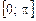 , приходится для вычисления интегралов по промежутку
, приходится для вычисления интегралов по промежутку 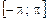 разбивать каждый из них на два интеграла – по
разбивать каждый из них на два интеграла – по 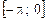 и по
и по 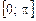 :
:
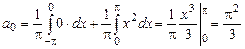 ;
;
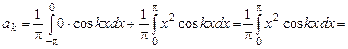
=( интегрируя дважды по частям) =
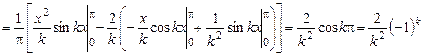 ;
;
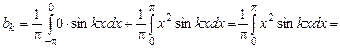
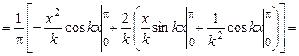
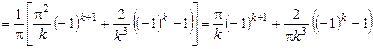 .
.
Так как значение выражения 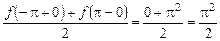 не совпадает со значением функции
не совпадает со значением функции 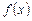 в точках
в точках 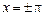 следовательно, равенство
следовательно, равенство
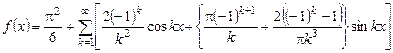
справедливо только для 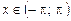 . На рисунке изображен график суммы ряда Фурье данной функции.
. На рисунке изображен график суммы ряда Фурье данной функции.
На этом примере видно, что функция, которая в двух разных половинах промежутка 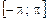 задавалась двумя разными аналитическими выражениями, может представляться во всем
задавалась двумя разными аналитическими выражениями, может представляться во всем 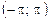 единым тригонометрическим рядом.
единым тригонометрическим рядом.
Ответ: 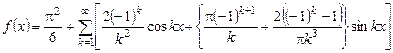 .
.
4.4. Вопросы для самопроверки
