Знакочередующиеся ряды. Знакопеременные ряды

[2, гл. XVI, § 7,8, упр. 20-26].

Пример. Исследовать сходимость ряда

,

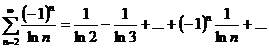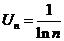
По теореме Лейбница ряд сходится, если выполнены два условия:

1) >

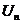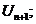
2)

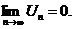
Проверим, выполнены ли эти условия для нашего ряда

< >

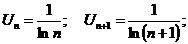
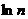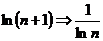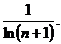
Первое условие выполнено.

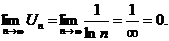
Второе условие выполнено, следовательно, ряд сходится условно.

Проверим, есть ли абсолютная сходимость, т.е. сходится ли ряд.

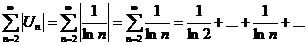
Используем признак сравнения сходимости рядов с положительными членами и сравним наш ряд с гармоническим рядом 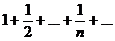, который расходится.

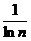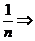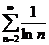> ряд тоже расходится и, следовательно, исходный ряд 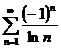абсолютно не сходится, а сходится только условно.

Функциональные ряды

[2, гл. XVI, § 9 - 12].

Степенные ряды

[2, гл. XVI, § 13, упр. 30, 31, 35-37].

Пример. Определить интервал сходимости ряда

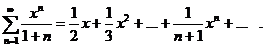
Решение. Коэффициенты ряда 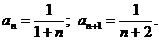Ищем радиус сходимости

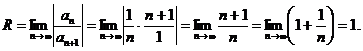
Следовательно, ряд сходится при 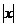<1 и расходится при 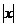>1. Исследуем отдельно точки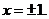

1) 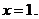В этой точке ряд равен

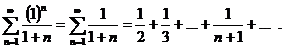
Используем интегральный признак сходимости. Заменим 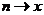. Тогда

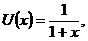
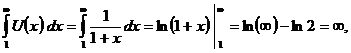
ряд расходится.

2) 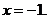В этой точке ряд равен

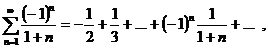
т.е. ряд знакочередующийся. По теореме Лейбница он сходится, действительно, здесь

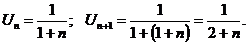
1) 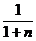> 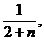т.е. > .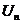

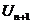2)

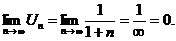
Ряд сходится. Интервал сходимости 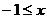< 1 или .

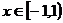Ряды Тейлора и Маклорена

[2, гл. XVI, § 16, 17, 19, 20, упр. 50, 51, 54-57.

Теория вероятностей.

Теория соединений

Теория соединений или комбинаторика рассматривает различные наборы множества элементов, выбранных из некоторого исходного набора множества этих элементов. Эти наборы составляются по определенным правилам и называются соединениями. Природа элементов, входящих во множество может быть любой, например, какие-то предметы, или люди, или числа и т.п. Нас, прежде всего, будет интересовать вопрос: сколько различных соединений можно составить? Рассмотрим самое простое соединение. Пусть исходное множество элементов разбито на k групп (наборов), содержащих n₁ , n₂ , ... , n_k элементов, т.е. первый набор n₁ элементов, второй n₂ элементов и т.д. Чтобы составить соединение из каждого набора следует взять один элемент. Сколько различных соединений можно составить? Очевидно каждый элемент первого набора может встретиться в соединении с каждым элементом второго набора и таких пар будет n₁n₂ . Каждая такая пара может встретиться с каждым элементом третьего набора, т.е. разных троек уже будет n₁n₂n₃ . Если обозначить за N число всех возможных соединений по одному элементу из каждого из k наборов, то получим

N = n₁ ∙ n₂ ∙ ... n_k .

Пример 1. В некотором городе телефонные номера состоят из буквы и пяти цифр. Буква может быть только А, В или Г. Первая цифра бывает 2, 3 , 4 или 5, а остальные цифры могут быть любые. Сколько телефонов может быть установлено в этом городе?

Решение. Первый набор состоит из трех букв, т.е. n₁ = 3 , второй - из четырех цифр, n₂ = 4. Следующие четыре набора содержат по 10 цифр, т.е. n₃ = n₄ = n₅ = n₆ = 10. Тогда всего различных номеров может быть N = 3´4´10´10´10´10 = 120 000.

В частном случае, если все k наборов содержат одинаковое количество элементов, скажем по n, то

N = n^k

Пример 2.Бросают две игральных кости. Сколько различных пар чисел может выпасть? (Нужно учесть, что 1 на первой кости и 2 на второй или 2 на первой и 1 на второй - это разные пары, т.е. разные соединения).

Решение. Так как у игральной кости, имеющей форму кубика, шесть граней, то n = 6, поэтому N = 6² = 36.

Отметим, что такие соединения могут получаться и в том случае когда имеется один набор из n элементов, из которого берут элемент, записывают его характеристику и возвращают в набор, после чего выбирают следующий элемент. В этом случае один и тот же элемент как бы выбирается из нового, но такого же как предыдущий, набора.

Теперь представим себе, что взятый один раз элемент обратно в набор не возвращается. Тогда второй элемент выбирается уже из набора, содержащего n - 1 элемент, третий из набора, содержащего n - 2 элемента и т.д. Это уже новый вид соединения, называемый размещением из n элементов по k элементов. Число размещений обозначается буквой А с двумя индексами

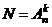
и читается “ а из эн по ка”

Каждое размещение отличается от другого или входящими элементами или их порядком. Например, из трех элементов a, b, c можно составить 6 размещений по 2 элемента ab, ac, bc, ba, ca, cb

Число различных размещений определяется формулой

.

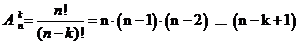Пример 3.В группе из 20 человек проводиться собрание. Сколькими способами можно избрать председателя, его заместителя и секретаря?

Решение. Очевидно, что важно не только кого изберут, но и на какие должности. Поэтому одно соединение от другого может отличаться или составом или порядком, т.е. это размещения, поэтому

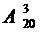= 20´19´18 = 6840

Если составлять размещения из всех n элементов, то очевидно они будут отличаться только порядком. Такие соединения называются перестановками из n элементов. Число перестановок обозначается P_n (“пэ из эн”) и, очевидно получается из 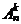при k = n, т.е.

P_n = n∙(n-1)∙(n-2) ... (n-n+1) = 1´2´3´…´n! = n! (“эн факториал”).

Пример 4.На трех карточках написаны цифры 1, 2, 3. Сколько различных трехзначных чисел можно составить переставляя местами эти карточки?

Решение. Очевидно, это число перестановок из трех, т.е.

Р₃ = 3! = 1´2´3 = 6.

Теперь рассмотрим соединения, которые называются сочетаниями из n элементов по k элементов. Это такие соединения, содержащие k элементов, взятых из данного множества из n элементов, которые отличаются только самими элементами (порядок роли не играет). Например, n = 3 : a, b, c , k = 2 тогда можно составить три сочетания ab, ac, bc. ( ab и ba - это разные размещения, но одно и то же сочетание). Число сочетаний обозначается буквой С. Очевидно, что для того чтобы составить все размещения нужно составить все возможные сочетания и в каждом произвести все возможные перестановки:

,

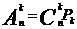где 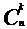- число сочетаний из n элементов по k элементов (“цэ из эн по ка”). Тогда

.

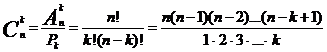Пример 5.На том же собрании 20 человек, где избирали председателя, заместителя и секретаря, нужно выбрать делегацию на конференцию в составе трех человек.

Решение. В этом случае порядок роли не играет, поэтому это не размещения, а сочетания и мы имеем

.

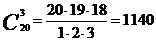Приведенные формулы числа размещений и числа сочетаний удобны для решения задач с конкретными числами n и k. Если задача решается в общем виде, то лучше пользоваться более компактными записями через факториалы, очень удобно ввести два определения

0!=1 и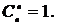

Событие и вероятность

[3. Введение, ч.1, гл.1, § 1 – 6].

Пример 1. В ящике 5 белых и 4 черных шара. Наудачу вынимают три. Какова вероятность, что среди них два белых и один черный шар?

Решение. Число всех возможных исходов - это число сочетаний из 9 по 3. Поэтому

.

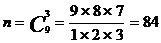Число вариантов выбора 2 белых из 4 белых - это число сочетаний из 4 по 2, то есть

,

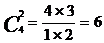и так как каждая пара может выпасть с любым из 4 черных шаров, то число благоприятных исходов равно произведению

m = 6∙4 = 24.

Тогда вероятность события “из ящика взяли 2 белых и 1 черный шар”

.

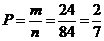Пример 2. На 10 карточках написаны цифры 1, 2, 3, 4, 5, 6, 7, 8, 9 и 0. Наудачу выбирают три карточки и раскладывают их в порядке появления. Какова вероятность, что получится число 120?

Решение. Поскольку в этом примере важен порядок цифр, то число всех возможных исходов

.

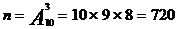Благоприятный исход только один, поэтому искомая вероятность

P 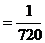.