Предел функции. Предел последовательности

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО РЫБОЛОВСТВУ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

"МУРМАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ"

Кафедра высшей математики
и программного обеспечения ЭВМ

ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИЙ. КОМПЛЕКСНЫЕ ЧИСЛА.
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ
ОДНОЙ ПЕРЕМЕННОЙ

Часть 2

Методические рекомендации к выполнению контрольных работ
для студентов 1 курса вечерне-заочного факультета
по дисциплине "Математика"

Мурманск

УДК 517 (076.5)

ББК 22.161Я73

М 54

Составители: В.С. Кацуба, канд. физ.-мат. наук, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ;

Л.Г. Мостовская, доцент кафедры высшей математики
и программного обеспечения ЭВМ МГТУ

Методические рекомендации рассмотрены и одобрены кафедрой
13 декабря 2006 г., протокол № 3

Рецензент – Ю.П. Драница, канд. физ.-мат. наук, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ

Оригинал-макет подготовлен в авторской редакции

Электронная верстка О.Р. Аптышевой

© Мурманский государственный технический университет, 2007

Оглавление

Введение.. 4

Методические указания по темАМ "Элементы теории функций. Комплексные числа" и "Дифференциальное исчисление функции одной переменной". 5

Справочный материал по теме "Элементы теории функций. Комплексные числа". 6

1. Функции и их свойства. 6

2. Предел функции. Предел последовательности. 9

3. Бесконечно малые, бесконечно большие и локально ограниченные функции 11

4. Вычисление пределов. 13

5. Раскрытие неопределенностей. 14

6. Непрерывность функции, точки разрыва. 16

7. Комплексные числа. 18

8. Действия над комплексными числами. 20

Примерный вариант и образец выполнения
контрольной работы 3. 21

Справочный материал по теме "Дифференциальное исчисление функциЙ одной переменной". 31

1. Дифференцирование функций. 31

2. Уравнения касательной и нормали к плоской кривой. 33

3. Вычисление пределов при помощи правила Лопиталя. 33

4. Исследование функций и построение графиков. 34

Примерный вариант и образец выполнения
контрольной работы 4. 38

Варианты контрольнЫХ работ.. 46

Варианты контрольной работы 3. 47

Варианты контрольной работы 4. 51

Рекомендуемая литература.. 54

Введение

В настоящем пособии содержатся методические рекомендации
к изучению теоретического материала и выполнению контрольных работ по темам "Элементы теории функций. Комплексные числа" и "Дифференциальное исчисление функций одной переменной", а также варианты
контрольных работ 3 и 4 по этим темам для студентов ВЗФ.

В результате изучения этих тем студенты 1-го курса должны:

• владеть понятиями функции, сложной и обратной функций, знать свойства основных элементарных функций, уметь определять их основные характеристики по графикам функций;

• знать определения предела функции и предела последовательности;

• уметь вычислять пределы, раскрывать неопределенности и анализи-ровать полученный результат с точки зрения определения предела;

• уметь исследовать функции на непрерывность, определять точки разрыва функции и устанавливать тип разрыва;

• знать, что такое мнимая единица и комплексное число, уметь производить операции над комплексными числами в алгебраической и тригонометрической формах;

• уметь решать простейшие алгебраические уравнения на множестве комплексных чисел;

• владеть основными понятиями дифференциального исчисления (производная и ее геометрический смысл, дифференциал), уметь находить производные функций, заданных явно, неявно или параметрически;

• иметь навыки решения основных задач с использованием производных: геометрические задачи на касательную и нормаль, вычисление пределов
с использованием правила Лопиталя и пр.;

• знать приемы исследования функций с помощью производной.

Данные методические рекомендации включают также список рекомендуемой литературы, справочный материал, необходимый для выполнения контрольных работ 3 и 4 для студентов 1-го курса и решение примерных вариантов этих работ, в которых имеются ссылки на используемый справочный материал.

Методические указания по темАМ
"Элементы теории функций. Комплексные числа"
и "Дифференциальное исчисление функции
одной переменной"

В таблице 1 приведены наименования тем в соответствии с содержанием контрольных работ и ссылки на литературу по этим темам. Перед выполнением каждой из контрольных работ рекомендуется изучить соответствующий теоретический материал и решить указанные в таблице задачи.

Таблица 1

№ к. раб.	№ задачи	Содержание (темы)	Литература
		Основные элементарные функции, их графики и основные характеристики. Сложные функции. Обратные функции	[1], гл. V, § 14; [2], гл. 4, § 1, 11, 12.1; [3], гл. VI, № 610–637; [4], гл. 4, № 15–38, 43–60, 62–71, 73–108, 151, 153
		Предел числовой последовательности и функции непрерывного аргумента. Вычисление пределов, раскрытие основных видов неопределенностей. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции	[1], гл. V, § 15–18; [2], гл. 4, § 2–6; [3], гл. VI, № 638–690, 692, 693, 700, 707, 714–719; [4], гл. 2, № 21–24, 26–28, 63–68, гл. 4, № 228–246, 285, 289, 346–351, 355, 358–359
		Определение непрерывности функции в точке и на промежутке. Точки разрыва функции и их классификация. Исследование функции на непрерывность	[1], гл. V, § 19; [2], гл. 4, § 7–9; [3], гл. VI, № 723–735
		Комплексные числа. Действия над комплексными числами в алгебраической и тригонометрической формах. Решение простейших алгебраических уравнений на множестве комплексных чисел	[1], гл. VI, § 27–28; [2], гл. 14, § 6.1; [4], гл. 9, № 1–52

Окончание табл. 1

№ к. раб.	№ задачи	Содержание (темы)	Литература
		Определение производной. Правила дифференцирования. Производные основных элементарных функций. Производные сложных функций. Дифференцирование функций, заданных неявно и параметрически. Производные высших порядков	[1], гл.V, § 20, 21, 23.1; [2], гл. 5, § 1, 4, 5, 7–9, 10.1, 11; [3], гл. VII, № 771–811, 900–907, 909–912, 950, 951, 964, 965, 969; [4], гл. 5, № 14–44, 162–167, 206–211
		Уравнения касательной и нормали к плоской кривой	[1], гл. V, § 20.2; [2], гл. 5, § 1.2; [3], гл. VII, № 917–921, 923–930; [4], гл. 5, № 139–144
		Вычисление пределов при помощи правила Лопиталя	[1], гл. V, § 25.2; [2], гл. 6, § 1, 2; [3], гл. VII, № 1024–1028, 1030–1040; [4], гл. 5, № 225–240, 258–264
		Монотонность и экстремумы функций. Выпуклость графика функции, точки перегиба. Вертикальные и наклонные асимптоты. Полное исследование функции и построение ее графика	[1], гл. V, § 25.3–25.8; [2], гл. 6, § 4; [3], гл. VII, № 1055–1058, 1061–1064, 1083–1084, 1091–1094, 1102–1109; [4], гл. 5, № 282, 293, 296, 297–300, 315–324, 334, 339, 342, 344–347

Примечание. Ссылки на литературу в таблице даны в соответствии
с номерами в списке рекомендуемой литературы.

Справочный материал по теме
"Элементы теории функций. Комплексные числа"

Функции и их свойства

Переменной называют величину x Î X, принимающую значения из некоторого множества значений Х.

Если каждому значению переменной х из множества Х поставлено
в соответствие по определенному правилу f единственное значение пере-менной у из множества Y, то говорят, что задана функция 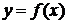, определенная на множестве Х с множеством значений Y. При этом используют следующие названия:

х – аргумент (независимая переменная);

у – значение функции (зависимая переменная);

Х – область определения функции (ООФ);

Y – множество значений функции (ОЗФ).

Функция 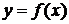, область определения Х которой симметрична
относительно начала координат, называется четной, если ,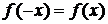
и называется нечетной, если , " .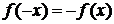

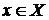Примеры. y = cos x – четная функция, y = x³ – нечетная функция, 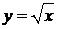– функция общего вида (ни четная, ни нечетная).

Функция 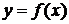называется периодической, если существует положительное число Т, такое, что 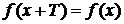, "x Î X.

Примеры. y = tg x – периодическая функция, наименьший период T = π, y = ln x – непериодическая функция.

Значение функции 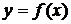– переменная величина, поэтому можно рассматривать новую функцию с аргументом у: z = g (y), где ,
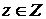т. е. функцию z = g (f (x)). Такая функция называется сложной функцией
от х, или суперпозицией функций f и g.

Пример. z = tg (х² + 3x – 1)– суперпозиция функций z = tg у
и у = х² + 3x – 1.

Если 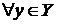ставится в соответствие единственное значение 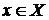, такое, что 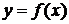, то говорят, что задана функция 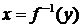, которую называют обратной по отношению к функции 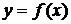. Функции f и 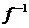называются взаимно обратными функциями. Если у обратной функции 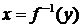обозначить аргумент буквой х, а функцию – буквой у,
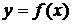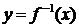то графики взаимно обратных функций и будут симметричны относительно прямой у = х.

Пример. y = lg x и y = 10^x – взаимно обратные функции.

Все функции, задаваемые аналитическим способом, можно разбить
на два класса: элементарные и неэлементарные. В классе элементарных функций выделяют основные элементарные функции: степенная (у = xⁿ), показательные (y = a^x), тригонометрические (y = sin x, y = cos x, y = tg x, y = ctg x), а также обратные к ним (логарифмические, обратные тригонометрические и др.). Элементарными называют функции, полученные из основных элементарных функций при помощи конечного числа операций сложения, вычитания, умножения, деления, а также суперпозиции основных элемен-тарных функций. Все остальные функции относятся к неэлементарным.

Примеры. y = lg (cos x) – элементарная функция, так как является суперпозицией основных элементарных функций y = lg x и y = cos x; 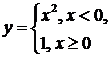– неэлементарная функция.

Нулями функции 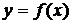называют точки х, в которых выполнено равенство 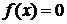. Нули функции – это абсциссы точек пересечения графика функции с осью Oх.

Пример. У функции y = lg (x) единственный нуль – точка х = 1.

Функция 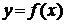называется монотонно возрастающей на интервале х Î (а; b), если для любых двух точек х₁ и х₂ этого интервала из неравенства х₂ > х₁ следует неравенство 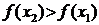, то есть если любому большему значению аргумента из этого интервала соответствует большее значение функции.

Функция 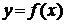называется монотонно убывающей на интервале х Î (а; b), если для любых двух точек х₁ и х₂ этого интервала из неравенства х₂ > х₁ следует неравенство .

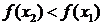Промежутки возрастания и убывания функции называются промежутками монотонности функции.

Если функция 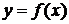монотонна на интервале х Î(а; b), то она имеет обратную функцию .

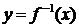Пример. Функция y = tg x монотонна на интервале 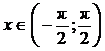, ее ОЗФ: 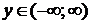. Она имеет обратную функцию y = arctg x, определенную на интервале 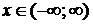, с ОЗФ: .

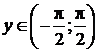Точка х₀ называется точкой максимума функции 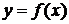, если суще-ствует такая двухсторонняя окрестность точки х₀, что для всякой точки х ¹ х₀ этой окрестности выполняется неравенство 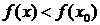. При этом число 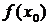называется максимумом функции 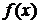и обозначается y_max.

Аналогично, если для всякой точки х ¹ х₀ из некоторой окрестности точки 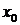выполняется неравенств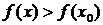о , то 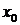называется точкой минимума, а число 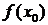– минимумом функции 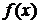и обозначается y_min.

Точки максимумов и минимумов называются точками экстремумов функции, а числа y_max и y_min называются экстремумами функции.

Пример. Функция y = cos x имеет точки максимумов x = 2pk, k = 0, ±1, ±2, …, 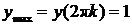, и точки минимумов x = p + 2pk, k = 0, ±1, ±2, …, .

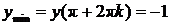Вычисление пределов

При вычислении пределов используют теоремы о конечных пределах и теоремы обесконечно малых и бесконечно больших функциях.

Раскрытие неопределенностей

Если некоторый предел существует, но не может быть вычислен при помощи теорем о конечных пределах или теорем обесконечно малых, бесконечно больших и локально ограниченных функциях, то говорят, что этот предел имеет неопределенность и указывают ее вид. Основные виды неопределенностей: .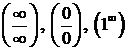

Чтобы вычислить предел, имеющий неопределенность, нужно предварительно преобразовать функцию, стоящую под знаком предела, таким образом, чтобы неопределенность исчезла, т. е. раскрыть неопределенность. Для этой цели рекомендуется использовать определенные правила.

Правило 1. Чтобы раскрыть неопределенность 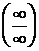при 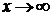, образованную отношением двух многочленов или иррациональных функций, нужно в числителе и знаменателе вынести за скобки старшие степени х
и сократить дробь на степень х.

Пример.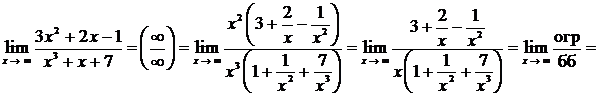

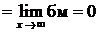(здесь использовано, что 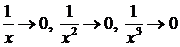при ).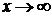

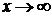Из правила 1 следует, что для раскрытия неопределенности при , образованной делением целых многочленов одинаковой степени, достаточно вычислить отношение коэффициентов при старших степенях переменной х:

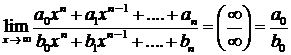. (8)

Правило 2. Чтобы раскрыть неопределенность при 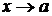, где а – число, образованную отношением двух функций, нужно в числителе
и знаменателе дроби выделить критический множитель (х – а), и сократить дробь на него.

Пример. 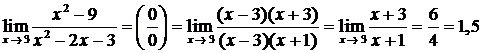(здесь критический множитель – это (х – 3), для его выделения использовано разложение многочленов на множители).

Для выделения критического множителя в случае, когда неопределен-ность образована отношением тригонометрических, показательных, или логарифмических функций, используют принцип замены бесконечно малых функций: при вычислении предела можно заменить любой бесконечно малый сомножитель на ему эквивалентный. При этом можно использовать теоретические соотношения эквивалентностей (см. формулы (1)–(7)).

Пример.

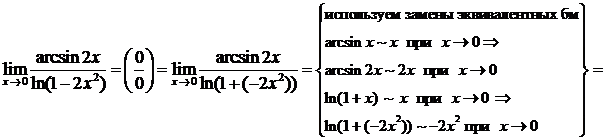
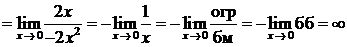(здесь критический множитель – это (х – 0) = х, для его выделения использован принцип замены эквива-лентных бесконечно малых и соотношения эквивалентностей (2) и (5)).

Правило 3. Чтобы раскрыть неопределенность (1^¥), нужно свести ее ко второму замечательному пределу, который может быть записан в двух формах:

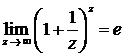или ;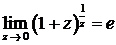

здесь е – это иррациональное число, которое можно представить в виде бесконечной непериодической десятичной дроби: е = 2,7182818… (e » 2,72).

Пример.

.

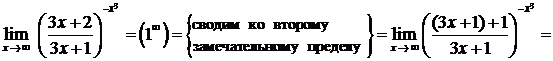
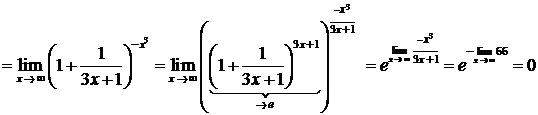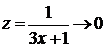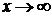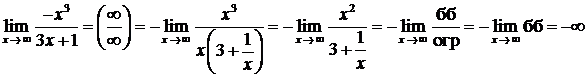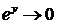При вычислении предела учтено, что при , , при .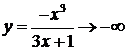

Комплексные числа

Комплексным числом называется выражение вида

z = x + iy, (10)

где х, у – действительные числа, а i – мнимая единица, т. е. число, для
которого выполнено равенство i² = –1.

Если х = 0, то комплексное число z = 0 + iy называется чисто мнимым.

Если у = 0, то комплексное число z = x + i0 = х является действительным, в частности, если х = у = 0, то z = 0.

На множестве комплексных чисел алгебраическое уравнение n-й
степени вида 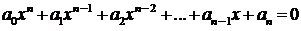, где a_k – числа, 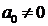,имеет ровно n корней.

Пример. Решим уравнение: х² + 9 = 0.

.

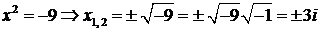Следовательно, уравнение имеет 2 корня: .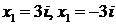

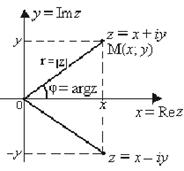На координатной плоскости Оху комплексное число z = x + iy можно изобразить точкой М(х; у) или радиус-вектором этой точки 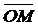(рис. 12), где х = Re z – действительная часть числа z, у = Im z – мнимая часть числа.

Рис. 12

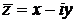Число называется сопряженным комплексному числу 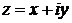. Геометрически точки z и 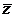симметричны относительно оси Ох (рис. 12).

Модулем комплексного числа называется действительное неотрицательное число 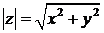. Геометрически модуль комплексного числа 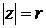– это модуль вектора 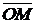(рис. 12).

Комплексное число можно задать либо парой действительных чисел (декартовы координаты точки (х; у)), либо его модулем и величиной угла φ между вектором 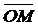и положительным направлением оси Ох (полярные координаты точки (r; φ)). Величина угла φ называется аргументом комп-лексного числа.

Аргумент комплексного числа определен неоднозначно, а с точностью до слагаемого 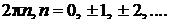. Значение аргумента, заключенное
в промежутке 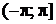, называется главным значением аргумента и обозначается arg z, тогда можно записать:

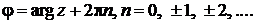(11)

Для комплексного числа z = 0 аргумент не определен, его модуль r = 0.

Запись комплексного числа в виде (10) называют алгебраической
формой комплексного числа.

Если использовать формулы связи между декартовыми и полярными координатами 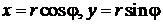, то можно записать тригонометрическую форму комплексного числа:

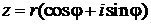, (12)

где

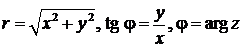. (13)

Для определения главного значения аргумента можно использовать формулы:

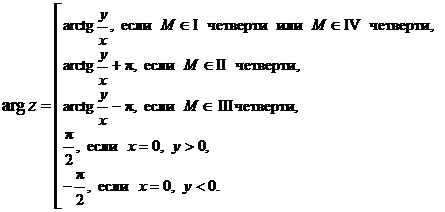(14)

Пример. Получим тригонометрическую форму комплексного числа z = –2 – 2i, используя формулы (13) и (14).

,

,

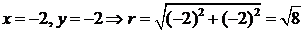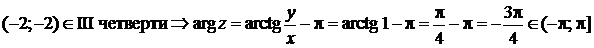следовательно, тригонометрическая форма комплексного числа z для 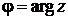имеет вид:

.

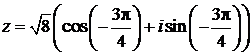Решение задачи 4

1) Найдем корни уравнения 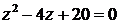на множестве комплексных чисел:

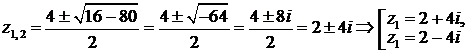
(здесь использовано: ).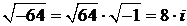

2) Чтобы найти комплексное число 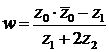, вычислим сначала :

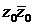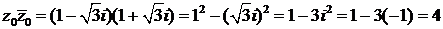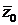( – это число, сопряженное числу 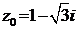, т. е. ).

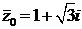Затем находим числитель 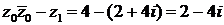и знаменатель .

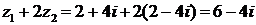Теперь вычисляем w, используя домножение числителя и знаменателя на число, сопряженное знаменателю:

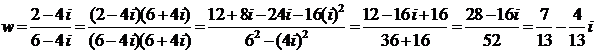– получили число w в алгебраической форме.

3) Комплексное число 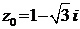задано в алгебраической форме z₀ = x + yi, где x = 1, y = 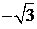. Получим тригонометрическую форму этого числа z₀ = r (cos j + sin j), используя формулы (13) и (14). Вычислим модуль комплексного числа 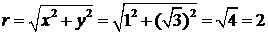и его аргумент:

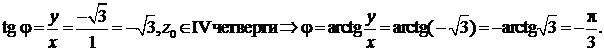
Таким образом, 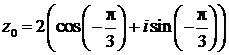– тригонометрическая форма числа z₀.

Для вычисления 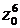используем формулу (15) возведения комплексного числа в натуральную степень:

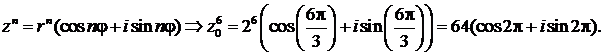
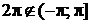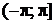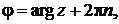
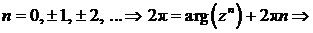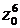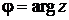Здесь аргумент . Выбираем главное значение аргумента, принадлежащее промежутку , используя формулу (11): при n = –1 получаем arg ( zⁿ ) = 0. Тригонометрическая форма комплексного числа для имеет вид:

.

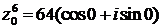Подставив значения cos 0 = 1, sin 0 = 0, получим алгебраическую форму этого числа: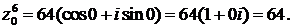

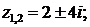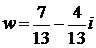Ответы: 1) 2) ; 3) ;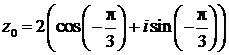

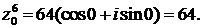
Справочный материал по теме "Дифференциальное исчисление функциЙ одной переменной"

Дифференцирование функций

Производной функции 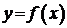в точке х называется конечный предел отношения приращения функции 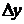к приращению аргумента Dx:

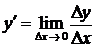, (16)

где .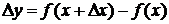

Другие обозначения производной: .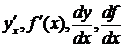

Если существует производная функции 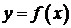в точке х, то функция называется дифференцируемой в этой точке. Дифференцирование функции – это процесс нахождения производной 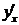. При дифференцировании используют таблицу производных и правила дифференцирования.

Таблица 3

Таблица производных основных элементарных функций

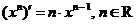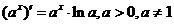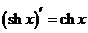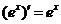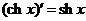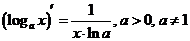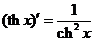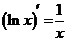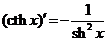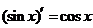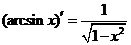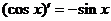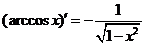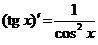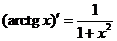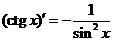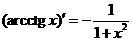Решение задачи 2

Найдем ординату точки касания: .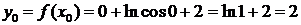

Для вычисления угловых коэффициентов касательной и нормали
найдем производную :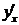

.

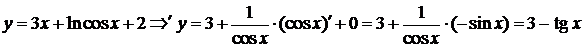Вычислим угловой коэффициент касательной: 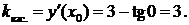Тогда угловой коэффициент нормали: .

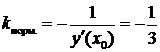Запишем уравнение касательной в точке М(0; 2) по формуле (23)
и приведем его к виду общего уравнения прямой:

.

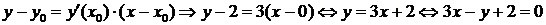Запишем уравнение нормали по формуле (24) и аналогично упростим его:

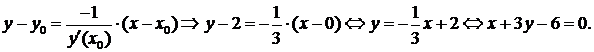
Для построения графика функции 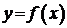в окрестности точки (х₀; у₀) вычислим значения функции 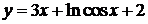в точках, близких к х₀ = 0:

,

.

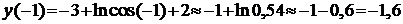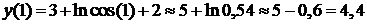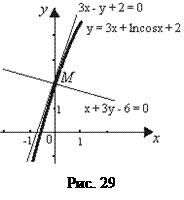
На рис. 29 построены участок графика функции 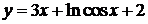, касательная 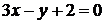и нор-маль 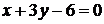в окрестности точки М(0; 2).

Ответы: 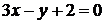и 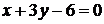. Графики на рис. 29.

Решение задачи 3а

В данном пределе функция 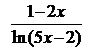при 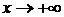есть отношение двух бесконечно больших функций, т. е. при вычислении предела нужно устранить неопределенность вида 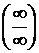. Используем правило Лопиталя (формула (25)):

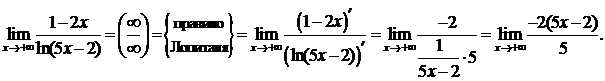
Последний предел есть предел бесконечно большой функции, т. е.

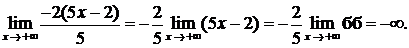
Следовательно, исходный предел .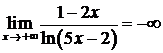

Решение задачи 3б

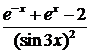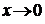В данном пределе функция при есть отношение двух бесконечно малых функций, т. е. при вычислении предела нужно устранить неопределенность вида . Используем правило Лопиталя:

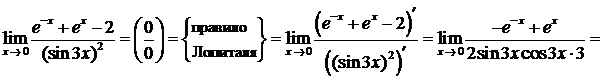
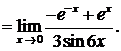
Последний предел при 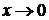есть отношение двух бесконечно малых функций, т. е. нужно снова устранять неопределенность вида . Еще раз используем правило Лопиталя:

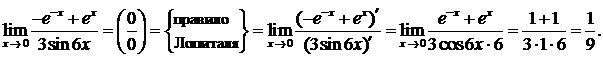
Следовательно, .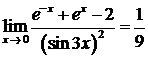

Ответы: а) 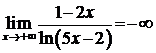; б) .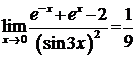

Решение задачи 4а

Проведем полное исследование функции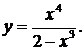

1) ООФ: 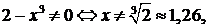т. е.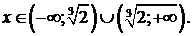

2) Функция не может быть четной или нечетной, так как имеет
несимметричную относительно начала координат ООФ. Следовательно, эта функция общего вида, симметрию графика предсказать нельзя. Функция непериодическая.

3) Функция непрерывна на всей ООФ, так как является элементарной функцией. Точка 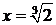является точкой разрыва, так как функция не определена в этой точке, но определена в ее окрестности.

Для определения типа разрыва найдем односторонние пределы при

:

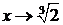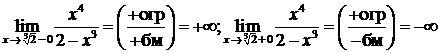
(здесь при 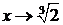числитель является ограниченной функцией, а знамена-тель – бесконечно малой). Следовательно, в точке 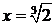функция терпит бесконечный разрыв и 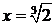– уравнение вертикальной асимптоты.

4) Промежутки монотонности и экстремумы найдем при помощи 1-й производной:

.

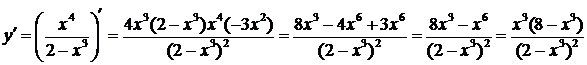Критические точки по 1-й производной: 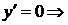х = 0, х = 2;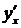
не существует .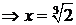

Точка 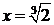не является критической точкой, так как 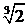Ï ООФ.
Следовательно, имеем две критические точки: х = 0 и х = 2.

Проверим выполнение достаточных условий монотонности и экстре-мума по знаку 1-й производной. На рис. 30 видно, что функция возрастает на интервалах 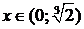и 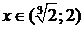, убывает на интервалах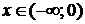
и .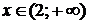

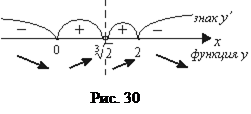В точке х = 0 есть минимум функции, 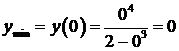, в точке х = 2 есть максимум, .

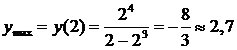5) Выпуклость, вогнутость графика и точки перегиба исследуем при помощи 2-й производной:

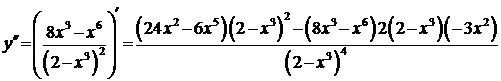
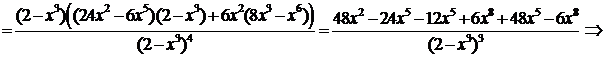
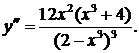
Критические точки по 2-й производной: 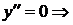х = 0, 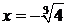; 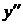не существует Þ x = 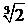. Точка 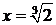не является критической точкой, так как 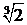Ï ООФ. Следовательно, критическими точками по второй
производной являются точки х = 0 и .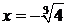

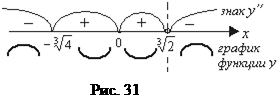Проверим выполнение достаточных условий выпуклости, вогнутости графика функции по знаку 2-й производной. На рис. 31 видно, что график функции выпуклый на интервалах 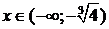, 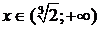и вогнутый на интервале 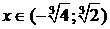. В точке
с абсциссой 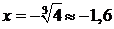имеется пере-гиб графика, .

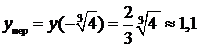6) Найдем наклонные асимптоты графика y = kx + b при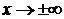
по формулам (26), (27):

;

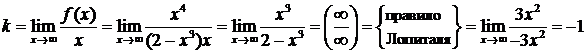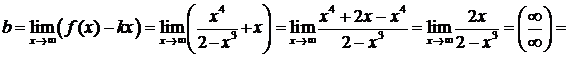
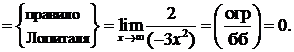
Следовательно, наклонная асимптота графика имеет уравнение .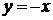

7) Точка пересечения с осями координат – единственная: (0; 0), так как

.

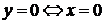8) 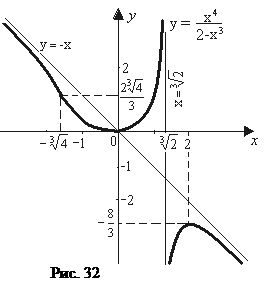Построение графика начинаем с построения асимптот 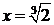и 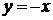, затем отмечаем точки графика, в которых функция имеет экстремумы: точку минимума (0; 0), точку максимума 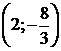, и точку перегиба 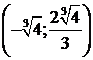. После этого выполняем построение гра-фика функции 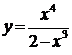сначала на промежутках 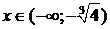и 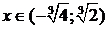, затем на промежутке .

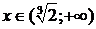На графике (рис. 32) видны сближение кривой с асимптотами при уда-лении от начала координат и перегиб кривой.

Ответ: график на рис. 32.

Решение задачи 4б

Проведем полное исследование функции .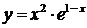

1) ООФ: 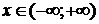, ОЗФ: 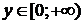, так как .

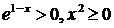2) Функция не является четной или нечетной, так как 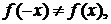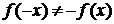. Следовательно, эта функция общего вида. Функция непериодическая.

3) Функция непрерывна на всей ООФ. Точек разрыва нет.

4) Промежутки монотонности и экстремумы найдем при помощи 1-й производной:

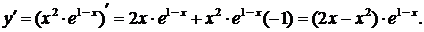
Критические точки по 1-й производной: