Раскрытие неопределенностей по правилу Лопиталя
I. Неопределенность 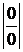 .
.
Теорема 1. Пусть
1) f и g определены и дифференцируемы в 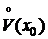 ,
, 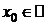 ;
;
2) g¢ (x)¹0 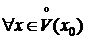 ;
;
3) 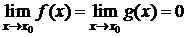 ;
;
4) существует конечный или бесконечный 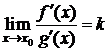 .
.
Тогда существует 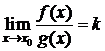 , т. е.
, т. е. 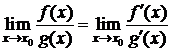 . (1)
. (1)
Доказательство.
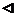 Т. к. f и g дифференцируемы в
Т. к. f и g дифференцируемы в 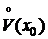 , то они непрерывны в
, то они непрерывны в 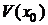 , кроме, быть может самой точки x0. Но если положить
, кроме, быть может самой точки x0. Но если положить 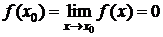 и
и 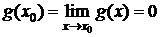 , то доопределенные таким образом функции f и g непрерывны в точке x0, т. е. в
, то доопределенные таким образом функции f и g непрерывны в точке x0, т. е. в 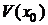 . Возьмем
. Возьмем 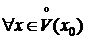 . Рассмотрим [x0;x], если x>x0 ([x;x0], если x<x0). Этот отрезок принадлежит
. Рассмотрим [x0;x], если x>x0 ([x;x0], если x<x0). Этот отрезок принадлежит 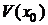 . Функции f и g на [x0;x] ([x;x0]) удовлетворяют условиям теоремы Коши. Тогда по этой теореме
. Функции f и g на [x0;x] ([x;x0]) удовлетворяют условиям теоремы Коши. Тогда по этой теореме
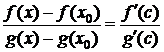 , где сÎ[x0;x] (или сÎ[x;x0]).
, где сÎ[x0;x] (или сÎ[x;x0]).
Т. к. f(x0)=g(x0)=0, то 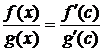 . (2)
. (2)
Пусть x®x0, тогда т. к. сÎ[x0;x] (или сÎ[x;x0]), то с®x0. По условию 4) 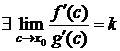 . Т. к. существует
. Т. к. существует 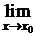 правой части равенства (2), то существует и
правой части равенства (2), то существует и 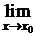 левой части, равный k. Переходя в (2) к
левой части, равный k. Переходя в (2) к 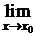 , получим (1).
, получим (1). 
Рассмотрим случай, когда  .
.
Теорема 2. Пусть
1) f и g определены и дифференцируемы в 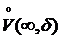 ;
;
2) g¢ (x)¹0  ;
;
3) 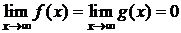 ;
;
4) существует конечный или бесконечный 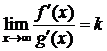 .
.
Тогда существует 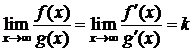 . (3)
. (3)
Доказательство.
 Используем теорему 1, применим замену
Используем теорему 1, применим замену 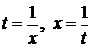 . Положим
. Положим 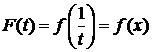 ,
, 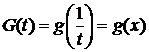 ,
, 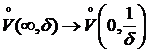 .
.
1) Функции F и G определены и дифференцируемы в 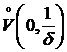 ,
,
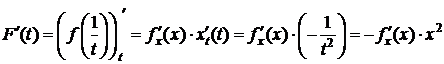 ,
, 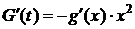 ;
;
2) G¢ (t)¹0 на 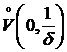 ;
;
3) 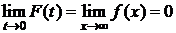 ,
, 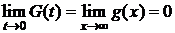 ;
;
4) 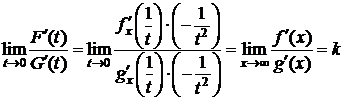 . (4)
. (4)
Т. о., функции F и G удовлетворяют условиям теоремы 1. Тогда
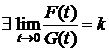 . (5)
. (5)
С другой стороны, 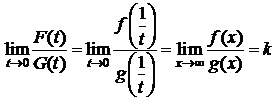 . (6)
. (6)
Из (4)-(6) следует (3). 
Из теорем 1 и 2 следует правило Лопиталя раскрытия неопределенностей  : предел отношения двух бесконечно малых функций при х®х0
: предел отношения двух бесконечно малых функций при х®х0 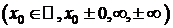 при выполнении условий 1)-4) теорем 1, 2 равен пределу при х®х0 отношения производных этих функций.
при выполнении условий 1)-4) теорем 1, 2 равен пределу при х®х0 отношения производных этих функций.
Пример 1.D 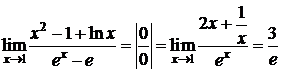 . D
. D
Замечание 1. Если условие 4) теорем 1, 2 не выполнено, правило Лопиталя может не действовать: 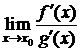 не существует, а
не существует, а 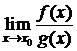 может существовать.
может существовать.
Пример 2. D 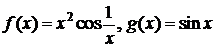 , х0=0.
, х0=0.
Для этих функций в 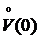 выполнены условия 1)-3) теоремы 1. Но
выполнены условия 1)-3) теоремы 1. Но 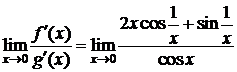 не существует, т.к. не существует
не существует, т.к. не существует 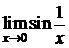 . Однако существует
. Однако существует 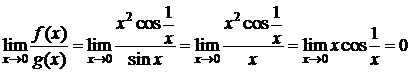 .D
.D
Замечание 2. Если производные f¢ и g¢ в окрестности 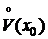 удовлетворяют тем же условиям , что и сами функции (условия 1)-4)), то правило Лопиталя можно применять повторно.
удовлетворяют тем же условиям , что и сами функции (условия 1)-4)), то правило Лопиталя можно применять повторно.
Пример 3.
D 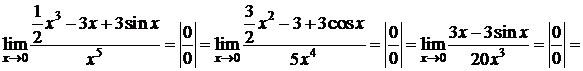
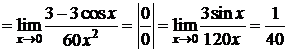 . D
. D
II. Неопределенность 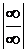 .
.
Теорема 3. Пусть
1) f и g определены и дифференцируемы в 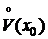 ,
, 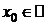 ;
;
2) g¢ (x)¹0 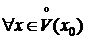 ;
;
3) 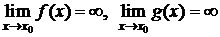 ;
;
4) существует конечный или бесконечный 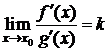 .
.
Тогда существует 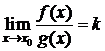 , т. е.
, т. е. 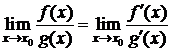 .
.
Из теоремы 3 следует правило Лопиталя раскрытия неопределенностей 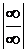 : предел отношения двух бесконечно больших функций при х®х0
: предел отношения двух бесконечно больших функций при х®х0 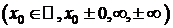 при выполнении условий 1)-4) теоремы 3 равен пределу при х®х0 отношения производных этих функций.
при выполнении условий 1)-4) теоремы 3 равен пределу при х®х0 отношения производных этих функций.
Остаются в силе замечания 1, 2.
Пример 4. D Пусть a>1.
а) 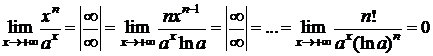 ;
;
б) 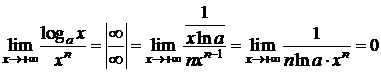 . D
. D
Вывод. Показательная функция ax (a>1) при 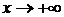 растет быстрее, чем степенная xn. Степенная функция xn при
растет быстрее, чем степенная xn. Степенная функция xn при 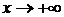 растет быстрее, чем логарифмическая logax (a>1).
растет быстрее, чем логарифмическая logax (a>1).
III. Неопределенности вида |0×¥|, |¥-¥|сводятся к неопределенностям вида 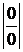 или
или 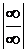 :
: 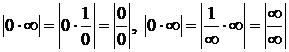 , |¥-¥| - привести к общему знаменателю.
, |¥-¥| - привести к общему знаменателю.
Пример 5. D 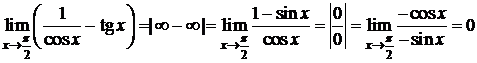 . D
. D
Пример 6.D 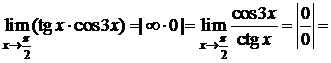
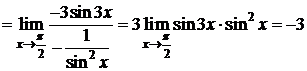 . D
. D
IV. Неопределенности 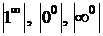 сводятся к |0×¥|, а она к
сводятся к |0×¥|, а она к 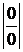 или
или 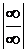 .
.
Пример 7.D  ;
;
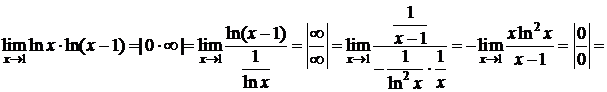
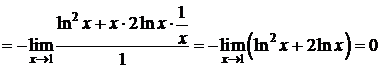 .
.
Следовательно, 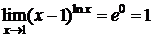 . D
. D
Пример 8. D 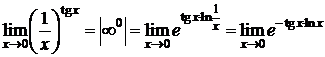 ;
;
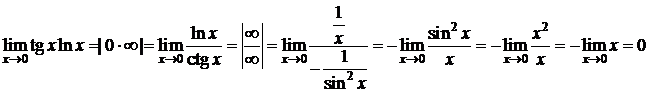 Значит,
Значит, 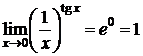 . D
. D
Замечание. Важно в случае многократного применения правила Лопиталя не забывать каждый раз проверять, раскрыта ли неопределенность, иначе можно допустить ошибку.
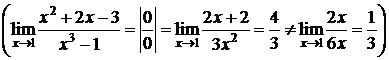
Формула Тейлора
Теорема. Пусть функция f(x) имеет в некоторой окрестности V(a) точки a производные до (n+1)-го порядка включительно. Пусть х – любая точка из V(a), p - произвольное положительное число. Тогда между точками а и х найдется такая точка с, что справедлива формула
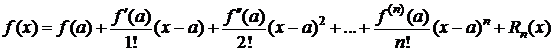 , (1)
, (1)
где 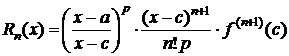 , cÎ(a;x) (или cÎ(x;a)). (2)
, cÎ(a;x) (или cÎ(x;a)). (2)
Формула (1) называется формулой Тейлора с центром в точке а, Rn(x) - остаточный член формулы Тейлора в общей форме.
Доказательство.
 Пусть j(x;a) - многочлен n - порядка относительно х правой части формулы (1), т. е.
Пусть j(x;a) - многочлен n - порядка относительно х правой части формулы (1), т. е.
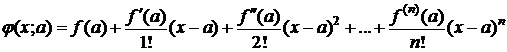 .
.
В силу условия j(x;a) существует. Обозначим через Rn(x)=f(x)-j(x;a). Тогда формула (1) будет доказана, если будет установлено, что Rn(x) имеет вид (2). Зафиксируем 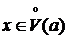 . Пусть x>a (для x<a доказательство аналогично). На отрезке [a;x] рассмотрим вспомогательную функцию y(t):
. Пусть x>a (для x<a доказательство аналогично). На отрезке [a;x] рассмотрим вспомогательную функцию y(t):
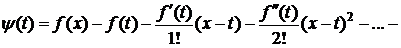
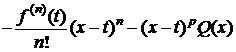 , (3)
, (3)
где 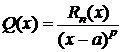 , т. е.
, т. е. 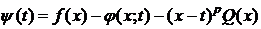 .
.
Покажем, что y(t) удовлетворяет условиям теоремы Ролля:
1) y(t) непрерывна на [a;x],
2) y(t) дифференцируема на (a;x),
3) 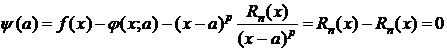 ,
,
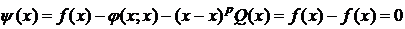 .
.
Значит, y(a)=y(x). Тогда на основании теоремы Ролля $ cÎ(a;x): y ¢(с)=0. Дифференцируя (3), получим
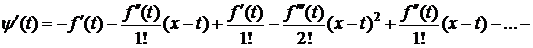
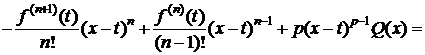
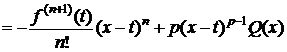 .
.
Тогда $ cÎ(a;x): 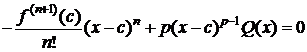 . Следовательно,
. Следовательно,
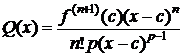 . (4)
. (4)
Тогда из (3), (4) следует
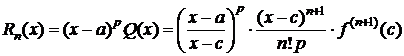 , cÎ(a;x).
, cÎ(a;x). 
Пример.1. Найти разложение по формуле Тейлора многочлена n-й степени
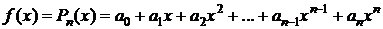 ,
, 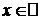 ,
, 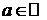 .
.
D fn+1(x)=Pn+1(x)=0 " 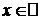 . Тогда Rn(x)=0 "
. Тогда Rn(x)=0 " 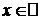 . Следовательно,
. Следовательно,
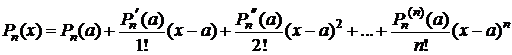 . D
. D
Остаточный член формулы Тейлора в различных формах
Преобразуем формулу (2). Т. к. cÎ(a;x), то существует такое число q, 0<q<1, что c=a+q(x-a) Þ x-c=x-a-q(x-a)=(x-a)(1-q). Тогда
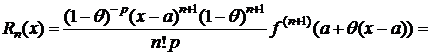
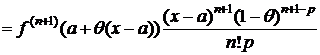 . (5)
. (5)
Частные случаи.
1) p=n+1 Þ 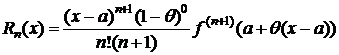 или
или
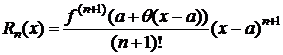 , 0<q<1. (6)
, 0<q<1. (6)
(6)– остаточный член в форме Лагранжа (наиболее употребительная форма).
2) p=1 Þ 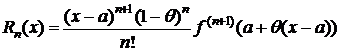 . (7)
. (7)
(7) – остаточный член в форме Коши.
Замечание 1. В формулах (6) и (7) q, вообще говоря, различны, т. к. эти формулы получены из (2) при различных значениях р, а q зависит от р.
Замечание 2. В некоторых задачах важен лишь порядок Rn(x) относительно (x-a).
Из (6) Þ 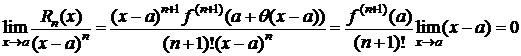
Þ 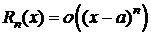 (8)
(8)
(8) - остаточный член в форме Пеано.
Замечание 3. С помощью формулы Тейлора можно производить приближенные вычисления f(x) с любой степенью точности: f(x)»j(x;a), погрешность равна Rn(x).
Замечание 4. Положим в (1) а=х0, х-х0=Dх, х=х0+Dх, f(x0+Dx)-f(x0)=Df(x0)=Dy.
Тогда 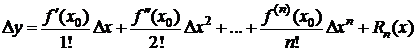 . Формула Лагранжа Dy=f(x)-f(x0)=f¢ (c)Dx является частным случаем формулы Тейлора и получается из нее при n=0. Действительно, при n=0
. Формула Лагранжа Dy=f(x)-f(x0)=f¢ (c)Dx является частным случаем формулы Тейлора и получается из нее при n=0. Действительно, при n=0
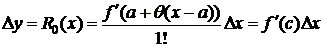 , 0<q<1.
, 0<q<1.
Формула Маклорена
Полагая в формулах (1), (6)-(8) а=0, получим
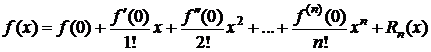 -
-
формула Маклорена;
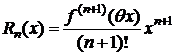 - форма Лагранжа;
- форма Лагранжа;
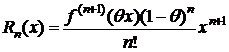 - форма Коши;
- форма Коши;
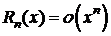 - форма Пеано.
- форма Пеано.
Разложение некоторых элементарных функций по формуле Маклорена
1. y=f(x)=ex, 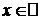 .
.
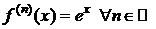 ,
, 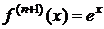 . При x=0 f(0)=f(n)(0)=1 Þ
. При x=0 f(0)=f(n)(0)=1 Þ
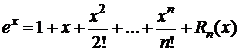 ,
,
где 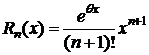 - форма Лагранжа;
- форма Лагранжа;
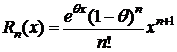 - форма Коши;
- форма Коши;
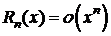 - форма Пеано.
- форма Пеано.
2. y=f(x)=sinx, 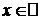 .
.
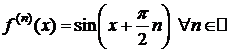 ,
,
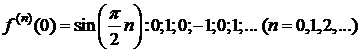 Þ
Þ
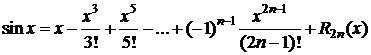 ,
,
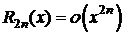 .
.
3.y=f(x)=cosx, 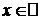 .
.
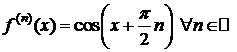 ,
, 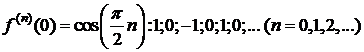 Þ
Þ
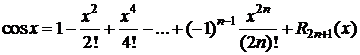 ,
,
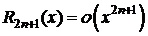 .
.
4. y=f(x)=ln(1+x), 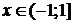 .
.
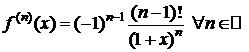 .
. 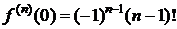 Þ
Þ
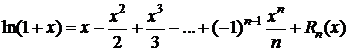 ,
,
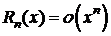 .
.
5. y=f(x)=(1+x)m, 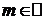 ,
, 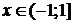 .
.
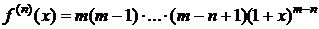 ,
, 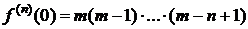 ,
,
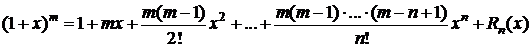 ,
,
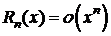 .
.
6. Пусть в случае 5 m=n 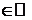 Þ
Þ 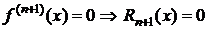 . Тогда
. Тогда
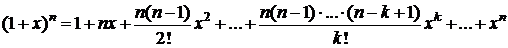 ,
,
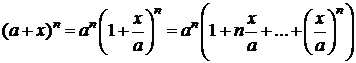 Þ
Þ
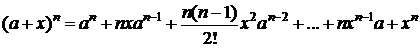 - бином Ньютона.
- бином Ньютона.
7. Пусть в случае 5 m=-1 Þ
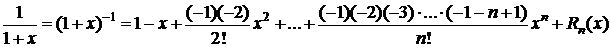 ,
,
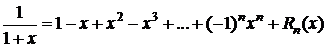 .
.
Положим здесь х=-х:
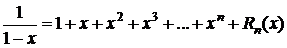 .
.
