Наибольшее и наименьшее значения функции в замкнутой области

Пусть функция z=ƒ(х;у) определена и непрерывна в ограниченной замкнутой области D. Тогда она достигает в некоторых точках D своего наибольшего М и наименьшего т значений (т. н. глобальный экстремум). Эти значения достигаются функцией в точках, расположенных внутри области D , или в точках, лежащих на границе области.

Правило нахождения наибольшего и наименьшего значений дифференцируемой в области D функции z = ƒ(х;у) состоит в следующем:

1. Найти все критические точки функции, принадлежащие D , и вычислить значения функции в них;

2. Найти наибольшее и наименьшее значения функции z = ƒ(х;у) на границах области;

3. Сравнить все найденные значения функции и выбрать из них наибольшее М и наименьшее т.

18. Условные экстремумы ф.м.п. Методы решения задач на условыне экстремумы.

Пусть функция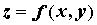определена в некоторой области 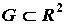и в этой области задана кривая уравнением 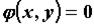. Условным экстремумом функции двух переменных 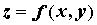называют ее экстремум при условии, что точки берутся на заданной кривой. Если из уравнения кривой можно, например, выразить 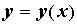, то задача о нахождении условного экстремума сводится к исследованию на экстремум функции одной переменной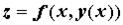

Методы решения задач на условный экстремум:

1. Если представляется возможным, то из уравнения связи 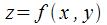В результате функция 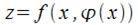преобразуется в функцию одной переменной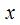

2.Метод множителей Лагранжа:

Если уравнение 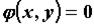не разрешимо ни относительно 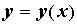ни относительно 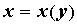, то рассматривают функцию Лагранжа 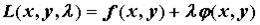. Необходимым условием существования условного экстремума функции 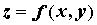при условии 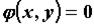является равенство нулю всех частных производных функции Лагранжа: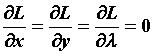

Пример: Найти экстремум функции f(x, y) = xy, если уравнение связи:

2x + 3y – 5 = 0

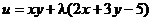
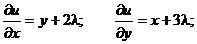
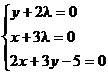
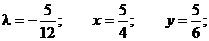
Таким образом, функция имеет экстремум в точке .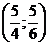

Использование функции Лагранжа для нахождения точек экстремума функции называется также методом множителей Лагранжа.

Выше мы рассмотрели функцию двух переменных, однако, все рассуждения относительно условного экстремума могут быть распространены на функции большего числа переменных.

19. Понятие об эмпирических формулах.Метод наименьших квадратов.

Эмпирические формулы — формулы, полученные из опыта посредством наблюдения и эксперимента. Имея серию исходных данных х1, x2, . . ., хn, в результате эксперимента получают соответствующие этим исходным данным результаты: y1, y2, ..., yn . Ставят задачу об отыскании такой функции из некоторого заранее заданного класса функций, чтобы отклонение этой функции от реальной зависимости было по возможности мало. Полученная зависимость называется Э. ф. Задача нахождения Э. ф. неоднозначна. Мерой отклонения функции f (х) от реальной зависимости считают

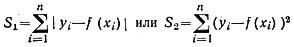
МНК:

Пусть в качестве исходных данных имеем таблицу:

x	x1	x2	…	xn
y	y1	y2	…	yn

содержащую статистические данные, или данные экспериментов. Если в качестве X выступает время, то имеем динамический ряд (тогда 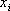размещены в возрастающем порядке). Необходимо получить аналитическую зависимость 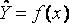(*) , которая наилучшим образом описывает начальные данные. Словосочетание «наилучшим образом», будем понимать в смысле минимума суммы квадратов отклонений значений 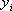, данных в таблице от 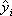, рассчитанных по (*): 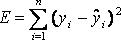(**).Определение зависимости (*) необходимо, в т.ч., и для нахождения 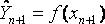что уже представляет собой задачу прогнозирования.

Нанесём точки из таблицы на координатную плоскость и сделаем предположение, что зависимость (*) есть линейной 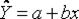, а отклонения от прямой вызваны 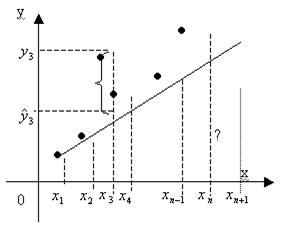Определим уравнение прямой (найдем значения коэффициентов a и b).

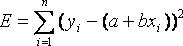Функция 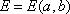.Продифференцируем 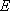по a и по b. Получим:

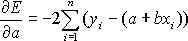
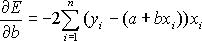
Для того, чтобы найти минимум функции E(a,b), приравняем нулю производные и упростим систему:

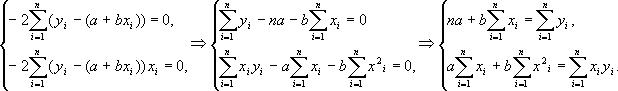
Находим а и b и подставляем.

20.Двойной интеграл.Его свойства.Вычисление двойного интеграла в декартовой и полярной системах координат.Геометрическое приложение двойного интеграла.

Двойные интегралы.

Определение: Если при стремлении к нулю шага разбиения области D интегральные суммы 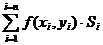имеют конечный предел, то этот предел называется двойным интеграломот функции f(x, y) по области D.

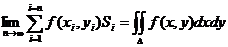
Т.к. деление области интегрирования произвольно, также произволен и выбор точек Р_i, то, считая все площади S_i одинаковыми, получаем формулу:

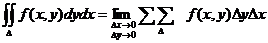
Условия существования двойного интеграла.

Сформулируем достаточные условия существования двойного интеграла.

Теорема. Если функция f(x, y) непрерывна в замкнутой области D, то двойной интеграл 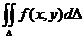существует.

Свойства двойного интеграла.

1)

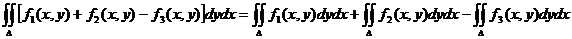
2)

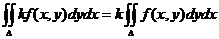
3) Если D = D₁ + D₂, то

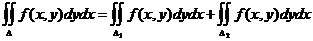
4) Теорема о среднем. Двойной интеграл от функции f(x, y) равен произведению значения этой функции в некоторой точке области интегрирования на площадь области интегрирования.

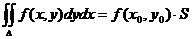
5) Если f(x, y) ³ 0 в области D, то .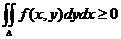

Вычисление двойного интеграла.

Теорема. Если функция f(x, y) непрерывна в замкнутой области D, ограниченной линиями х = a, x = b, (a < b), y = j(x), y = y(x), где j и y - непрерывные функции и

j £ y, тогда

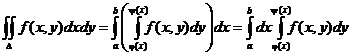
Теорема. Если функция f(x, y) непрерывна в замкнутой области D, ограниченной линиями y = c, y = d (c < d), x = F(y), x = Y(y) (F(y) £ Y(y)), то

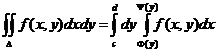
20. Выражение 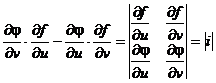называется определителем Якобиили Якобианомфункций f(u, v) и j(u, v).

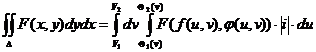Формула замены переменной в двойном интеграле :