Наибольшее и наименьше значения функции в замкнутой области

Значение, принимаемое функцией в некоторой точке множества, на котором эта функция задана, называется наибольшим (наименьшим) на этом множестве, если ни в какой другой точке множества функция не имеет большего (меньшего) значения. Н. и н. з. ф. по сравнению с её значениями во всех достаточно близких точках называются экстремумами (соответственно максимумами и минимумами) функции. Н. и н. з. ф., заданной на отрезке, могут достигаться либо в точках, где производная равна нулю, либо в точках, где она не существует, либо на концах отрезка. Непрерывная функция, заданная на отрезке, обязательно достигает на нём наибольшего и наименьшего значений; если же непрерывную функцию рассматривать на интервале (т. е. отрезке с исключенными концами), то среди её значений на этом интервале может не оказаться наибольшего или наименьшего. Например, функция у = x, заданная на отрезке [0; 1], достигает наибольшего и наименьшего значений соответственно при x = 1 и x = 0 (т. е. на концах отрезка); если же рассматривать эту функцию на интервале (0; 1), то среди её значений на этом интервале нет ни наибольшего, ни наименьшего, так как для каждого x0 всегда найдётся точка этого интервала, лежащая правее (левее) x0, и такая, что значение функции в этой точке будет больше (соответственно меньше), чем в точке x0. Аналогичные утверждения справедливы для функций многих переменных

Двойной интеграл

Понятие интеграла может быть расширено на функции двух и большего числа переменных. Рассмотрим, например, функцию двух переменных z = f (x,y). Двойной интеграл от функции f (x,y) обозначается как

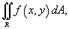
где R - область интегрирования в плоскости Oxy. Если определенный интеграл 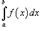от функции одной переменной 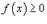выражает площадь под кривой f (x) в интервале от x = a до x = b, то двойной интеграл выражает объем под поверхностью z = f (x,y) выше плоскости Oxy в области интегрирования R

Повторный интеграл

понятие интегрального исчисления. Вычисление двойного интеграла

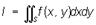
от функции f (x, у) по области S, ограниченной прямыми х = а, х = b и кривыми y = φ1(x), у = φ2(х), при некоторых условиях относительно функций f (x, у), φ1(x), φ2(х), производится по формуле:

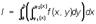
где при вычислении внутреннего интеграла х считается постоянным.

Тройной интеграл

Тройным интегралом называют кратный интеграл с d=3.

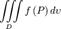
Здесь 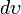— элемент объема в рассматриваемых координатах.

В прямоугольных координатах 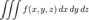, где 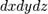является элементом объема в прямоугольных координатах.

Якобиан

функциональный определитель ½aik½1n с элементами 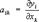, где yi = fi (X1,..., Xn), l £ i £ n, — функции, имеющие непрерывные частные производные в некоторой области А; обозначение:

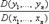
Якобиан часто применяется при анализе неявных функций

Равенство определителя Якоби нулю служит удобным необходимым и достаточным условием вырожденности преобразования координат, а неравенство его нулю — необходимым и достаточным условием невырожденности.

Замена переменных

Для вычисления двойного интеграла иногда удобнее перейти в другую систему координат.

Это может быть обусловлено формой области интегрирования или сложностью подынтегральной функции.

В новой системе координат вычисление двойного интеграла значительно упрощается.

Замена переменных в двойном интеграле описывается формулой

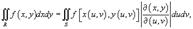
где 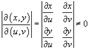выражение представляет собой так называемый якобиан преобразования 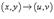, а S − образ области интегрирования R, который можно найти с помощью подстановки 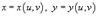в определение области R. Отметим, что в приведенной выше формуле 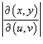означает абсолютное значение соответствующего определителя.

Двойной интеграл

Пусть область D ограничена линией r = r( ) и лучами = и = , где и r – полярные координаты точки на плоскости, связанные с ее декартовыми координатами x и y

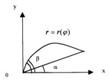
Рис. 5

соотношениями 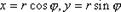(рис. 5). В этом случае

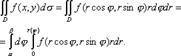
Замечание. Если область D в декартовых координатах задается уравнением, содержащим бином , например, и т.д., то вычисление двойного интеграла по такой области удобнее производить в полярных координатах.

Если область D в декартовых координатах задается уравнением, содержащим бином 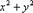, например, 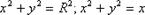и т.д., то вычисление двойного интеграла по такой области удобнее производить в полярных координатах.