Уравн. с разделяющимися переменными

Ду 1-го порядка назыв уравн с раздел перемен,если его можно привести к виду:

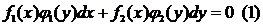- Диф. ур с раздел переменными.

Где f₁ (х)и f₂ (х)зависят только от х, и f₁ (у)и f₂ (у)от y,разделим обе части уравнения (1) на f₁ (у)и f₂ (х)в предположении что f₂ (х) f₁ (у) 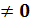получим

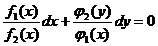- ур с разд перемен, т.к. при dx нах-ся ф-ция зависящ тока от x, при dy от y

взяв неопр интегр получ: 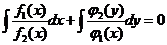- общими интегралами исходного диф. уравнения.

Однородные ДУ 1-ого порядка

Функция f(x,y) называется однородной функцией n–го измерения, если при любом t выполняется условие: .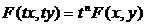

Дифференциальное уравнение y’=f(x,y) есть однородное, если функция f(x,y) является однородной функцией нулевого измерения.

Дифференциальное уравнение P(x,y)dx+Q(x,y)dy=0 однородное, если P(x,y) и Q(x,y) являются однородными функциями одного и того же измерения.

P(x,y)dx=-Q(x,y)dy; 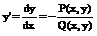. Однородное уравнение всегда можно привести к виду 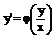и с помощью замены y/x=t однородное уравнение всегда приводится к уравнению с разделяющимися переменными (y/x=t; y=xt; y’=t+xt’).

Такие уравнения с помощью подстановки y = ux и y' = u'x + u, dy=udx+xdy , где u – новая переменная сводятся к уравнениям с разделяющимися переменными u и х.

Пример. Найти общее решение (общий интеграл) дифференциального уравнения y`=2xy/(x²-y²). Проверим, является ли данное уравнение однородным:

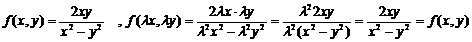т.е. является. Введем замену: 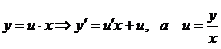. Подставим в исходное уравнение: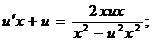

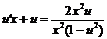
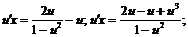
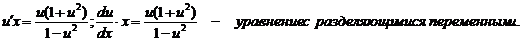
Разделим переменные и проинтегрируем полученное уравнение: 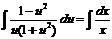. Найдем интеграл левой части уравнения:

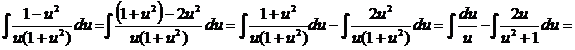
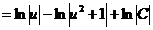. Найдем интеграл правой части уравнения: 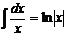. Приравняем найденные результаты: 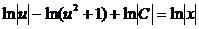. Используем свойства логарифмов и потенцируем равенство: 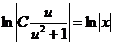, 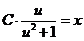. Подставим вместо 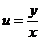получим 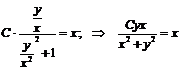.Общее решение данного дифференциального уравнения имеет вид: 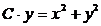, где С – произвольная постоянная.

7.Линейные ДУ 1-ого порядка (метод подстановки Бернулли, метод вариации произвольной постоянной Лагранжа).

ЛДУ- уравнения вида y’+P(x)y=f(x) (21)– первого порядка относительно у и у’. Где P(x) и f(x) заданные ф-ции, линейн относ неизв ф-ции и ее произв-й. Если f(x)=0 , то ур-ние линейн однородн.

Для решения ЛДУ применяем замену(подстановка Бернулли): y=UV, тогда y’=U’V+UV’

U’V+UV’+P(x)UV=f(x)

V(U’+P(x)U)+UV’=f(x) (23)

Далее приравняем U’+P(x)U=0 – ур с раздел. переменными, его общ решен:

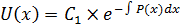, подстав U(x) в 23: 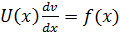;(поделим обе части на U(x) и проинтегрир): 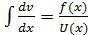; ;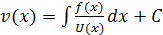подставл найден знач v(x) и u(x) в выр

y(x)=U(x)V(x): y(x)= U(x)( );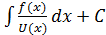

По методу вариац произв постоян неодн ду (21) ищется в виде: 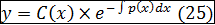--реш. неоднор лду в котор C=C(x)-диференц ф-ция. подставив в 21 получим:

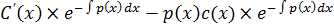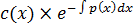+p(x) =f(x)

=>

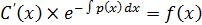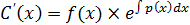
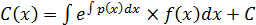; ф-ция с(х) найдена подст в ф-лу 25 оконч получ общ реш ду 21:

y=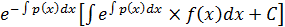

Уравнение Бернулли

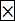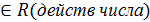урав вида y’+P(x)y=Q(x) yⁿ,n (26)

при n=0, оно превр в линейн ду, при n=1 в ур с раздел перемен.

y’+ 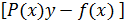y=0 –ур с разд перем

рассм случ когда 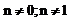ур Берн сведется к лин диф ур, для этого обе части рав-ва 26 раздел все эл-ты на yⁿ ; y 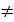0; y=0 – явл решен ур Берн при n=0; yⁿ 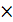y’+P(x) y^1-n=f(x) (27). Введем замену перемен: y^1-n=z, z=z(x), z’=(1-n)y; y^-n 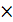y’= 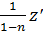; Ур 27 примет вид:

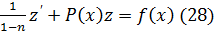; 28 явл лин ду относ задан ф-ции z(x) его реш мож быть получ метод подстан Берн или вариац произв постоян.