Уравнения с разделяющимися переменными.

Эти уравнения самые простые. При решении какого-либо уравнения его стараются свести к уравнению с разделяющимися переменными.

А. Уравнение с разделенными переменными

Уравнением с разделенными переменными называется уравнение вида:

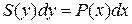(1)

Переменные разделены, каждая из них находится только в той части равенства, где ее дифференциал. 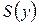и 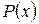– заданные функции.

Теорема. Общим интегралом уравнения (1) служит соотношение 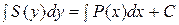. (2)

Пример. Найти общий интеграл уравнения .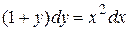

Решение. 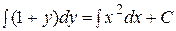или 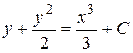– общий интеграл.

Теорема. Частным решением уравнения (1), удовлетворяющим начальному условию 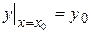будет функция 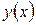, определенная из равенства 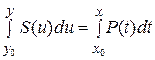. (4)

Пример. Найти решение уравнения 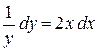, удовлетворяющего условию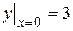

Решение. .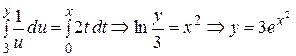

В. Уравнения с разделяющимися переменными

Уравнением с разделяющимися переменными называется уравнение вида: 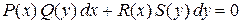(5)

В этом уравнении легко разделить переменные. Для этого поделим уравнение на произведение 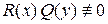. Тогда получим: 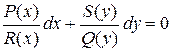. (6)

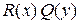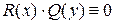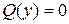Это уравнение с разделенными переменными. При переходе от уравнения (5) к уравнению (6) мы могли потерять некоторые решения, которые обращают в нуль произведение , именно или . (7)

Уравнение (7) есть конечное (без производных) уравнение относительно 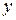. Его решением служат 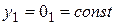, , 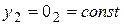… и т.д. Заметим, что константы 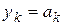служат решениями уравнения (5), т.к. 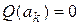и .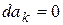

Общим интегралом (5) будет 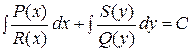. (8)

Если решения 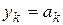получаются из (8) при подходящем выборе С, то такие решения суть частные, если же подобрать нужное С невозможно, то они особые решения.

Следовательно, если у уравнения (5) есть особые решения, то соответствующие им графики, т.е. интегральные кривые – это прямые параллельные оси ОХ.

Частным решением уравнения (5), удовлетворяющим начальному условию 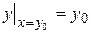будет функция 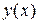, определенная уравнением:

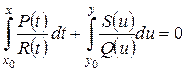. (9)

Пример. Для уравнения 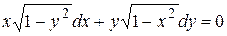найти общий интеграл и частное решение, удовлетворяющее условию .

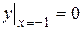Решение.

а) Общий интеграл. Делим на . .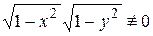

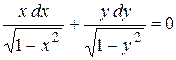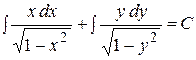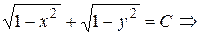Отсюда или – общий интеграл.

б) Частное решение.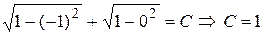

Частное решение: .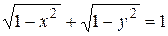

с) Особое решение.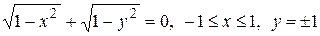

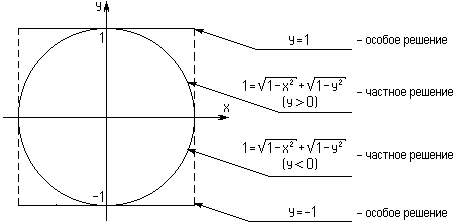Возможна потеря решений 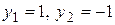. Оба эти решения особые.

Однородные уравнения.

Определение. Уравнение 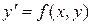(1) называется однородным, если 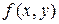может быть представлена как функция отношения своих аргументов, т.е. 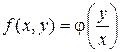. (2)

Таким образом, однородное уравнение имеет вид: 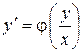(3)

Теорема. Однородное уравнение (3) имеет общий интеграл: 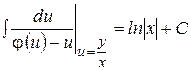. (4)

Замечание 1. В доказательстве теоремы мы предполагаем, что 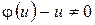. Рассмотрим тот случай, когда 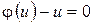. Здесь имеются две возможности.

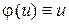а) Тогда 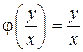и уравнение (3) принимает вид: .

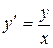Это уравнение с разделяющимися переменными 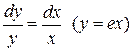и здесь никаких преобразований делать не нужно.

б) уравнение 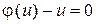удовлетворяется лишь при определенных значениях 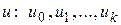. В этом случае могут быть потеряны решения 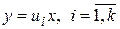. Интегральные кривые суть прямые, проходящие через начало.

Пример. Решить уравнение .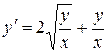

Решение. Уравнение однородное. Полагаем . .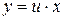

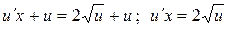Если 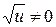, то 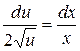. Отсюда .

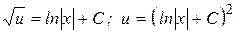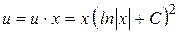– общий интеграл.

Может быть потеряно решение 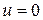или .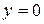

Действительно, 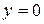есть решение рассматриваемого уравнения и оно не может быть получено из общего интеграла ни при каком значении С, следовательно 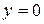есть особое решение.

Замечание 2. Формулу (4) запоминать не следует. Надо уметь ее выводить в каждом конкретном случае, как это сделано в примере.

Замечание 3. Для интегрирования уравнения более общего вида, чем (3) 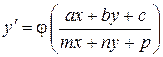. (6)

(обобщенное однородное) сначала делают замену неизвестной функции и независимой переменной по формулам 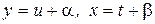; выбирая 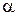и 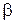такими, чтобы исчезли свободные члены в числителе и знаменателе аргумента 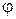в (6), тогда (6) приводится к однородному уравнению.

Линейные уравнения

Определение. Линейным дифференциальным уравнением I порядка называется дифференциальное уравнение вида: 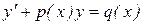(1),

где 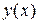– неизвестная функция аргумента.

Уравнение (1) линейно относительно 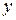и .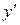

Если 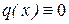, то уравнение (1) примет вид: 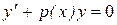(2), и называется линейным однородным. При этом уравнение (1) называется линейным неоднородным.

Уравнение (2) называется линейным однородным, соответствующим линейному неоднородному уравнению (1).