Уравнением с разделяющимися переменными

Дифференциальное уравнение первого порядка y' = f(x,y) называется уравнением с разделяющимися переменными, если функцию f(x,y) можно представить в виде произведения двух функций, зависящих только от x и y:

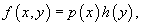
где p(x) и h(y) − непрерывные функции.

Рассматривая производную y' как отношение дифференциалов 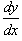, перенесем dx в правую часть и разделим уравнение на h(y):

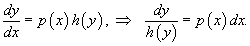
Разумеется, нужно убедиться, что h(y) ≠ 0. Если найдется число x₀, при котором h(x₀) = 0, то это число будет также являться решением дифференциального уравнения. Деление на h(y) приводит к потере указанного решения.

Обозначив 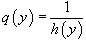, запишем уравнение в форме:

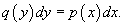
Теперь переменные разделены и мы можем проинтегрировать дифференциальное уравнение:

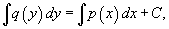
где C − постоянная интегрирования.

Вычисляя интегралы, получаем выражение

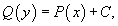
описывающее общее решение уравнения с разделяющимися переменными.

2.Дифференциальные уравнения с разделенными переменными

Рассмотрим дифференциальное уравнение вида:

f1(x)dx=f2(y)dy, (1)

которое называется уравнением с разделенными переменными.

Пусть найдено некоторое его решение y(x). При подстановке y=y(x) в дифференциальное уравнение (1) оно обратится в тождество и, интегрируя его, имеем

∫f1(x)dx=∫f2(y)dy+C, (2)