Миноры, алгебраические дополнения. Теорем о разложении определителя по элементам ряда

Миноры, алгебраические дополнения. Теорем о разложении определителя по элементам ряда

Миноры и алгебраические дополнения. Теорема Лапласа

Минором Мij квадратной матрицы n-го порядка для элемента аij называется определитель (n-1)-ого порядка, полученный с данного вычёркиванием i-ой строки и j-ого столбца.

Алгебраическое дополнение элемента 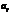определителя 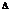определитель

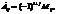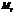где - минор

элемента .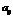

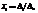
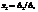
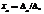
Теорема Лапласа. В данной квадратной матрице А(n x n ) вычеркнем k строк (1£k£n). Тогда равно сумме произведений всевозможных миновров к-того порядка из данных строк на их алгебраические дополнения: 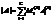. То же для столбцов. Теорема удобна для матриц с большим кол-вом нулей.

Обратная матрица. Необходимое и достаточное условия существования обратной матрицы

Определим операцию деления матриц как операцию, обратную умножению.Опр.Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию:

XA = AX = E,где Е - единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратнойк матрице А и обозначается А^-1.Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну. Рассмотрим общий подход к нахождению обратной матрицы.Исходя из определения произведения матриц, можно записать:AX = E Þ 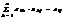, i=(1,n), j=(1,n), e_ij = 0, i ¹ j,

e_ij = 1, i = j .Таким образом, получаем систему уравнений: 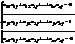Решив эту систему, находим элементы матрицы Х.

9 Ранг матрицы. Теорема об инвариантности ранга матрицы.

Ранг матрицы

Рангом матрицы А наз наивысший из порядков миноров этой матрицы не равных нулю.А=(аij)=(a11 a12 … a1n; a21 a22 … a2n; …; am1 am2 … amn) m*x Возьмем и выделим какой-нибудь минор порядка А (а11 а12; а21 а22). Если этот минор не равен нулю то его строки(столбцы) линейно независимы, тогда первые 2-е строки этой матрицы линейно независ. Ранг матрицы А будет не меньше 2-х. При нахождении ранга матрицы пользуются методом окомляющих миноров. Этот метод состоит в том что минор второго порядка окомляют одной строкой и одним столбцом, т.е строят минор 3-го порядка. Если же миноры 3-его порядка окомляющие данный минор 2-го порядка равны нулю, то матрица А не содержит миноров порядка большего 2-х, не равных нулю и ее ранг равен 2-м.Если же есть хотя бы один минор 3-го порядка который не равен нулю, то ранг матрицы не менее 3-х и процедуру окомления 3-порядка продолжают, в итоге будет найден минор 4-го порядка не равный нулю. Для которого все окомляющие миноры n+1-го порядка равны нулю. Тогда ранг матрицы А равен n. Разность матрицы обозн. R(A). Замечания: 1)Ранг нулевой матрицы равен нулю; 2)ранг матрицы равен max числу его линейно независимых строк.

Теорема (об инвариантности ранга при элементарных преобразованиях): Введём обозначение А~В для матриц, полученных друг из друга элементарными преобразованиями. Тогда справедливо утверждение: Если А~В, то их ранги равны.

Базис и координаты вектора.

Базисом на плоскости называется совокупность фиксированной точки и 2х неколлинеарных векторов, проведенных к ней.

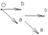Базисом в пространстве наз. совокупность фиксированной точки в пространстве и 3х некомпланарных векторов.

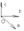Любой вектор на плоскости может быть разложен по векторам базиса на плоскости. Любой вектор в пространстве может быть разложен по векторам базиса в пространстве.

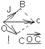ОС=OA+OB, OA=x*i, OB=j*y, OC=xi+yj. Числа х,у наз-ся координатами вектора ОС в данном базисе

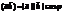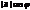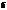17. Скалярное произведение векторов: его свойства скаляр проивед векторов называется произведение их модулей на косинус угла между ними. Оно обозначается . – есть проекция на и 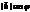– проекция 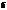на . Скалярное произведение векторов есть произведение одного из них на проекцию другого на первый. Косинус угла между векторами:

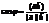
Два вектора на 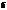перпендикулярны (ортогональны), т.е. 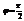тогда и только тогда, когда .

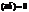Свойства скалярного произведения:

1. 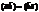– переместительное свойство;

2. 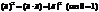– скалярный квадрат вектора;

3. 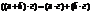– распределительное свойство;

4. 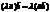– сочетательное свойство относительно числового множителя.

Докажем распределительное свойство: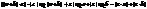

Гипербола и ее св-ва.

Кривая 2го порядка наз. гиперболой, если в ур-ии Ax²+Cy²=d, коэффициент А и С имеют противоположные знаки, т.е. А*С<0

б) Если d>0, то каноническое ур-е гиперболы примет вид: x²/a²-y²/b²=1, F1(c,o) и F₂(-c,0) - фокусы ее, e>0, e=c/a - эксцентриситет.

Св-во:
для любой точки гиперболы абсолютная величина разности ее расстояний до фокусов есть величина постоянная = 2а.

б) если d=0, ур-е примет вид x²/a²-y²/b²=0, получаем 2 перекрестные прямые х/а±у/b=0

в) если d<0, то x²/a²-y²/b²=-1 - ур-е сопряженной гиперболы.

Парабола и ее свойства.

Множество точек плоскости, координаты которых по отношению к системе декартовых координат удовлетворяет уравнению y=ax², где х и у - текущие координаты, а- нек. число, наз. параболой.

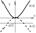Если вершина нах. в О(0,0), то ур-е примет вид

y²=2px-симметрично отн. оси ОХ

х²=2pу-симметрично отн. оси ОУ

Точка F(p/2,0) наз. фокусом параболы, а прямая x=-p/2 - ее директриса.

Любой точке М(х,у), принадлежащей параболе, расстояние до фокуса = r=p/2

Св-ва:

1. парабола предст. собой ¥ точек плоскости, равноотстающих от фокуса и от директрисы y=ax².

Угол между плоскостями

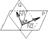
N₁,N₂-нормальные векторы плоскости.

P:A₁x+B₁y+C₁z+D₁=0

Q:A₂x+B₂y+C₂z+D₂=0

P^Q{A₁,B₁,C₁}

Q^N₂{A₂,B₂,C₂}

Угол между плоскостями

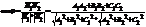
1)Пусть P^Q<=>N₁^N₂

A₁A₂+B₁B₂+C₁C₂=0 условие перпендикулярности P^Q.

2) Пусть P^Q<=> N₁^N₂

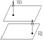
A₁/A₂=B₁/B₂=C₁/C₂- Условие параллельности 2х плоскостей.

A₁/A₂=B₁/B₂=C₁/C₂=D₁/D₂- Условие совпадения 2х плоскостей.

Й, замечательный предел.

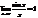Доказательство: докажем для 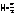справедливость неравенства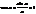

В силу четности входящих в неравенство ф-ий, докажем это неравенство на промежутке 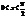Из рисунка видно, что площадь кругового сектора

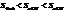
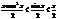, так как х>0, то ,

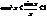2. следовательно, что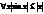

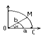
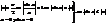
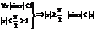
1. Покажем, что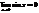

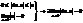
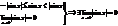
2. Докажем, что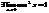

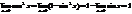
3. Последнее утверждение:

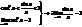
Второй замечательный предел

lim(n®¥)(1+1/n)^n=e Док-во:

x®+¥ n x:n=[x] => n£x<n+1 => 1/(n+1)<1/x<1/n

Посколько при ув-нии основания и степени у показательной ф-ции, ф-ция возрастает, то можно записать новое неравенство (1/(n+1))^n£(1+1/n)^x£ (1+1/n)^(n+1) (4)

Рассмотрим пос-ти стоящие справа и слева. Покажем что их предел число е. Заметим (х®+¥, n®¥)

lim(n®¥)(1+1/(n+1))=lim(n®¥)(1+1/(n+1))^n+1-1= lim(n®¥)(1+1/(n+1))^n+1*lim(n®¥)1/(1+1/(n+1))=e

lim(n®¥)(1+1/n)^n+1= lim(n®¥)(1+1/n)^n* lim(n®¥)(1+1/n)=e*1=e

48. Непрерывность функции в точке. Действия над непрерыв функциями

x=x₀+Dx, Dx=x-x₀

Dy=f(x₀+Dx)-f(x₀)

Ф-ция y=f(x) наз. непрерывной в точке x₀, если она определена в окрестности этой точки, а limDy=0. (бесконеч.малая. приращению аргумента соответствует б.м. приращению ф-ции).

limDy=lim[f(x)-f(x₀)]=limf(x)-limf(x₀)=0, то

limf(x)=limf(x₀)

x®x₀

Ф-ция непрерывна в точке х₀, если ее предел = значению этой ф-ции в точке х₀

Ф-ция явл. непрерывной на интервале, если она непрерывна в каждой его точке.

Асимптоты.

Опр. Часть графика называется бесконечной ветвью если при движении точки по этой части, расстояние между ей и началом координат стремится к бесконечности.

Опр. Прямая называется асимптотой бесконечной ветви графика функции, если при удалении точки от начала координат по этой ветви, расстояние до данной прямой стремится к нулю.

Теорема 1: x=a (вертикальная прямая) – является асимптотой для бесконечно вертикальной ветви графика функции y=f(x), тогда когда f(x)®µ, при x®a.

Теорема 2: Критерий существования наклонной асимптоты прямая y=kx+b является асимптотой для правой (левой) ветви графика функции тогда, когда существует предел при :

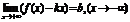
Док-во: Точка M0(x0,y0) и прямая

L: Ax+By+Cz=0, то расстояние

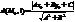
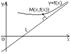Пусть y=kx+b

асимптота =>

d(M,l)®0=>

kx-f(x)+b®0

тогда f(x)-kx®b

при x®+µ

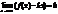существует предел:

Миноры, алгебраические дополнения. Теорем о разложении определителя по элементам ряда