Миноры и алгебраические дополнения.

Опр.1:Минорами элемента 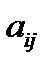квадратной матрицы А называется определитель матрицы получ. из матрицы А вычеркиванием i-той строки и j-того столбца, обозначается 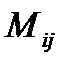.Алгебраическим дополнением элемент.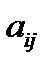назыв. число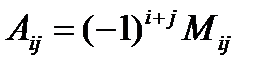

С учетом опр. 1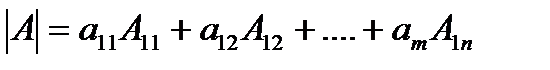

Теорема 1 .Определитель квадратной матрицы n-го порядка = сумме произв.какой-либо строки(столбца) наихалгебр.дополнений: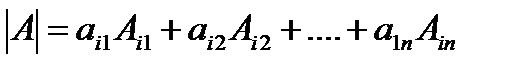

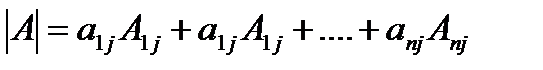
Доказательство: докажем для строк (для столбцов аналогично).Если i=1, то справедливость теоремы следует из определения детерминанта и алгебраич.дополнений.

Пусть i 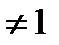, переставив i-тую строку на 1 место и обозначив 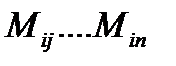миноры элементы i-той строки матрицы А.

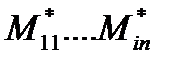миноры элемент.1 строки получ.матрицы.Тогда 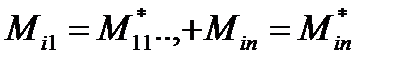- определитель матрицы А равен:

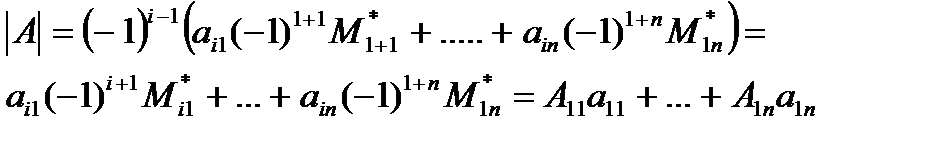
Представл.опред.матрицы как в теор.1 назыв.разложением по строке(столбцу).

Теорема 2.Сумма произведений элементов какой-либо строки определителяn–го порядка на алгебраические дополнения элементов другой его строки равна нулю, т. е.

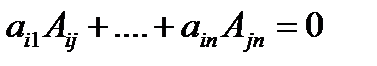,при i, j = 1, 2, . . . , n и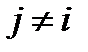

Доказательство. Рассмотрим вспомогательную матрицу:

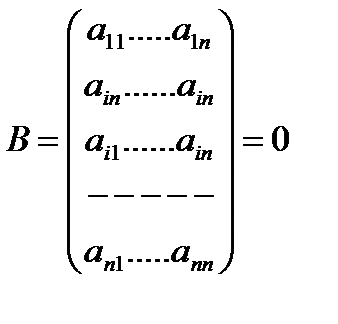
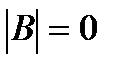
Заметим что алгебр.дополнения элементов j-той строки матриц 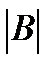= 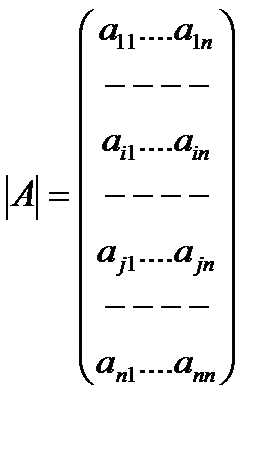равны.

Разложим определитель матрицы В по элементам j строки: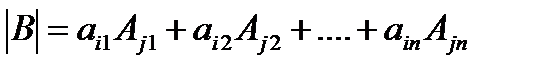

5.Обратная матрица.Критерии её сущ-ния.
Обратная матрица.ПустьА кв. матрица n-го порядка. Матрица В наз. Обратной матрице А, если в произведении получается единица А*В=В*А=Е. Обратную матрицу можно обозначить А^-1 , таким образом А* А^-1= А^-1*А=Е. Квадратная матрица А наз. невырожденной , если detA≠0. Если detA=0, то матрица наз. невырожденной. Теорема. Если кв. матрица А имеет обратную, то А- невырожденная матрица. Обратно, если А- невырожденная матрица, тоА обладает обратной матрицей, причем А^-1= 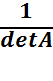*A^*где, A^*- присоединенная матрица, т.е. матрица 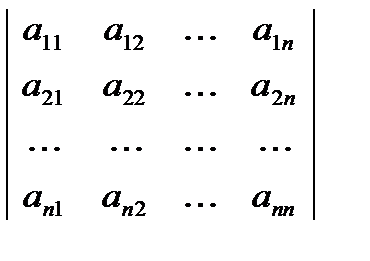,составленная из алгебраических дополнений элементов матрицыА и протранспонированная.

6.Ранг матрицы.Элементарные преобразования матриц.Нахождения ранга с их помощью
Ранг матрицы. Пусть 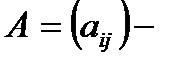матрица размера 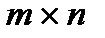. Если в этой матрице выбрать произвольно 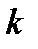строк и 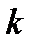столбцов 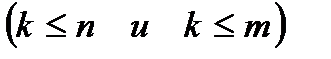, то элементы, стоящие на пересечении этих строк и столбцов, образуют квадратную матрицу порядка k. Определитель этой матрицы называется минором k - го порядка матрицы А.Натуральное число 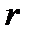называется рангом матрицы А, если 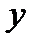нее имеется минор порядка r , отличный от нуля, а все миноры порядка r+1 равны нулю. Если ранг матрицы равен r, то всякий минор порядка r, отличный от нуля, называют базисным минором.

Имеет место следующая теорема:Если в матрице А имеется минор 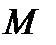-порядка r, отличный от нуля, а всякий минор порядка r+1, включающий все элементы минора 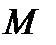(окаймляющий минор), равен нулю, то ранг матрицыА равен r .

При вычислении ранга матрицы находим некоторый минор k-го порядка, отличный от нуля. Затем вычисляем только миноры порядка k+1, окаймляющие этот минор; если все они равны нулю, то ранг матрицы равен k. Практически этот способ нахождения ранга матрицы весьма трудоемок. Укажем еще один способ вычисления ранга матрицы, основанный на применении так называемых элементарных преобразований матрицы

Элементарными преобразованиями матрицы называют следующие преобразования:

1) Умножение всех элементов строки на одно и то же число;

2) Перестановка двух строк;

3) Вычеркивание одной из двух пропорциональных строк;

4) Вычеркивание строки, состоящей из одних нулей;

5)Прибавление ко всем элементам какой-либо строки соответствующих элементов другой, умноженных на одно и то же постоянное число;

6) Те же операции со столбцами.

Справедлива следующая теорема:

Ранг матрицы не меняется в результате элементарных преобразований, примененных к матрице.

Любую матрицу можно элементарными преобразованиями привести к диагональной форме. Тогда ранг матрицы равен числу отличных от нуля элементов диагонали.