Миноры и алгебраические дополнения

Если в матрице 3-го порядка вычеркнуть строку и столбец, то определитель, порождённый оставшейся матрицей 2-го порядка, называется минором того элемента, на котором пересекаются вычеркнутые ряды.

Алгебраическим дополнением элемента называется минор этого элемента, умноженный на (-1)^p , где р – сумма номеров рядов, пересекающихся , пересекающихся на нашем элементе.

Теорема разложения. Определитель 3-го порядка равен сумме парных произведений элементов парных произведений элементов любого ряда на их алгебраические дополнения.

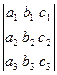= a₁ A₁ + a₂ A₂ + a₃ A₃.

Операции над матрицами.

Матрицы подобно векторам можно склады­вать, умножать на число и друг на друга. Рассмотрим эти операции:

1°. Суммой двух матриц А = (a_ij) и В = (b_ij) с одинаковым ко­личеством m строк и n столбцов называется матрица С = (c_ij), элементы которой определяются равенством a_ij + b_ij = c_ij, (i = 1, 2, … , m; j =1, 2, ... , n).

Обозначение: A + В = С.

Пример 1.

+ = = .

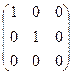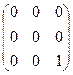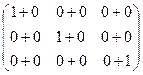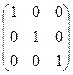Аналогично определяется разность двух матриц. a_ij – b_ij = c_ij,

Обозначение: A – В = С.

Свойства операции сложения матриц:

1) коммутативность: А + В = В + А.

2) ассоциативность: (А + В) + С = А + (В + С).

3) Дистрибутивность: k×(А + В) = k×А + k×В, (k + t)×А =k×А + t×А

2°. Произведением матрицы А = (a_ij) на число k, называется мат­рица, у которой каждый элемент равен произведению соответствую­щего элемента матрицы А на число k: k×А = k×(a_ij) = (k×a_ij), (i = 1, 2, … , m; j =1, 2, ... , n).

Пример 2.

3× = = .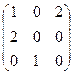

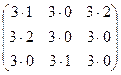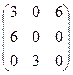3°. Произведением матрицы А = (a_ij), имеющей m строк и k столбцов, на матрицу В = ((b_ij), имеющую k строк и n столбцов, называется матрица С = (c_ij), имеющая m строк и n столбцов, у которой элемент c_ij равен сумме произведений элементов i-й стро­ки матрицы А и j-го столбца матрицы В, т. е.

c_ij = a_i1 b_1j + a_i2 b_2j + … + a_ik b_kj (i = 1, 2, … , m; j =1, 2, ... , n).

При этом число k столбцов матрицы А должно быть равно числу строк матрицы В. В противном случае произведение не определено. Произведение обозначается так: А×В = С.

Пример 3.

× = = .

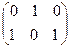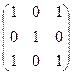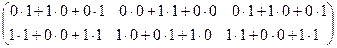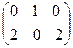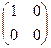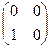Пример 4. Пусть А = , В = , тогда А×В = 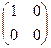× 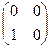= 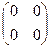, а

В×А = × = .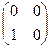

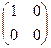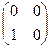Отсюда получаем, что А×В ¹ В×А, т. е. умножение матриц не обладает перестановочным свойством.

Непосредственной проверкой можно убедиться, что для суммы и произведения матриц справедливы следующие соотношения:

(А + В)×С = А×С + В×С; С×(А + В) = С×А + С×В; (А×В)×С = А×(В×С);

4°. Умножение на единичную матрицу. Совокупность элемен­тов а₁₁, а₂₂, … , а_nn rвадратной матрицы А = (a_ij) называется глав­ной диагональю матрицы. Матрица, у которой элементы, стоящие на главной диагонали, равны единице, а все остальные элементы рав­ны нулю, называется единичной матрицей и обозначается буквой Е.

Так, единичной матрицей третьего порядка является матрица

Е =

Единичная матрица обладает замечательным свойством, а имен­но: умножение квадратной матрицы любого порядка на соответству­ющую единичную матрицу не меняет матрицу. Это свойство и объяс­няет ее название «единичная»: при умножении матриц она обладает таким же свойством, как число 1 при умножении чисел.

А×Е = Е×А = А

Ранг матрицы.

Рангом матрицы А называют наивысший порядок отличных от нуля миноров матрицы А.

Пример.

A = 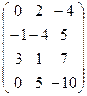меняем местами 1 и 2 столбцы: A ~ 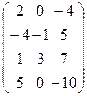, затем умножаем первую строку на ½: А ~ 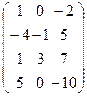, прибавляем к 3 столбцу удвоенный первый столбец: А ~ 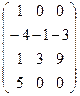. Умножим 1 строку на 4 и сложим со 2-й строкой, затем на (-1) и сложим с 3-й, и наконец, на (–5) и сложим с 4-й. В результате этих элементарных преобразований получится матрица, эквивалентная исходной:

А ~ . Далее последовательно будем преобразовывать строки и столбцы матрицы, не меняя 1-й строки и 1-го столбца:

1) умножим 2-ю строку на (–1);

2) умножим 2-ю строку на (–3) и сложим с 3-й строкой;

3) умножим второй столбец на (–3) и сложим с 3-м столбцом. В результате этих элементарных преобразований последовательно получаются матрицы:

~ ~ .

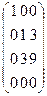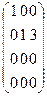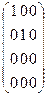Не все миноры 2-го порядка равны 0, а значит rang (А) = 2.