Потенциальное (безвихревое) поле

Если во всех точках поля ротор равен нулю, то поле называется безвихревым.

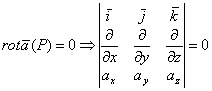. Потенциал поля,Тогда выражение a_xd_x+a_yd_y+a_zd_z является полным дифференциалом некоторой функции u(x,y,z), т.е

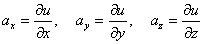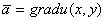Тогда Функция u называется потенциалом векторного поля, а градиент ее направлен по касательной к векторной линии.Справедливо и обратное утверждение. Поле градиента любой функции u(x,y,z)является потенциальным, а сама функция u - его потенциалом.В потенциальном поле циркуляция по любому замкнутому контуру равна нулю.Потенциальное поле вполне определяется его потенциалом.

Если мы возьмем замкнутую векторную линию и рассмотрим циркуляцию вдоль этой замкнутой линии, то 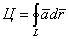где 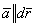Тогда, 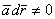Итак, циркуляция вдоль замкнутой векторной линии не равна нулю. Следовательно, в безвихревом поле 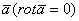не могут существовать замкнутые векторные линии при условии, что области ими ограниченные целиком лежат в векторном поле.Трубчатое (соленоидальное) поле Векторное поле, для всех точек которого дивергенция равна нулю, называется трубчатым или соленоидальным. Возьмем в этом поле какую-нибудь площадку S₁ и проведем через каждую точку ее границы векторные линии. Эти линии ограничивают часть пространства, называемую векторной трубкой По условию 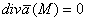. Тогда по формуле Остроградского-Гаусса имеем:

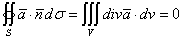где V - тело, ограниченное векторной трубкой.

Это значит, что поток вектора 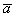в направлении векторных линий соленоидального поля один и тот же, т.е. через каждое сечение протекает одно и то же количество жидкости, поэтому векторные линии не могут начинаться или обрываться внутри области G, а векторные трубки такого поля либо замкнуты, либо выходят на границы области, где определен вектор .

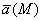57. Дифференциальные уравнения 1 порядка, задача Коши.

Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида

F(x, y, y' )=0,

где F — известная функция трех переменных, определенная в области G из R³, x — независимая переменная из интервала (a, b), y(x) — неизвестная функция, y'(x) — ее производная.

Обыкновенные дифференциальные уравнения, разрешенные относительно производной, т.е. уравнения вида

y'=f(x, y)

называют уравнениями в нормальной форме.

Задача Коши. Заключается в нахождении решения u (x, t); х = (x₁,..., x_n) дифференциального уравнения вида:

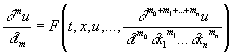, (1)

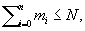m₀ < m, m > 0,

удовлетворяющего т. н. начальным условиям.

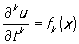, t = t₀, x Î G₀, k = 0, …, m-1, (2)

где G₀ — носитель начальных данных — область гиперплоскости t = t_o пространства переменных x₁,..., x_n. Когда F и f_k, k = 0,..., m — 1, являются аналитическими функциями своих аргументов, задача Коши (1), (2) в некоторой области G пространства переменных t, х, содержащей G₀, всегда имеет и притом единственное решение. Однако это решение может оказаться неустойчивым (т. е. малое изменение начальных данных может вызвать сильное изменение решения), например в том случае, когда уравнение (1) принадлежит эллиптическому типу.