Метод Фурье для уравнения колебаний

Пусть нам дана конечная, однородная струна, закреплённая на концах (т.е. в точках x=0 и x=l). Если на неё не действуют внешние силы, то функция u(x,t), дающая закон колебания струны должна удовлетворять уравнению:

.

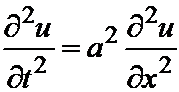Граничным условиям:

u(0,t)=0; u(l,t)=0.

И начальным условиям:

.

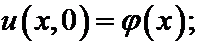
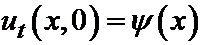Здесь сформулирована 1-я краевая задача. Видно, что как само уравнение, так и дополнительные условия (граничные) однородны, поэтому если некоторые функции удовлетворяют уравнению и граничным условиям, то и любая их линейная комбинация также удовлетворяет этому уравнению и граничным условиям. На этом и основан метод Фурье. Суть его заключается в том, что на первом этапе мы находим некоторый запас функций, удовлетворяющих уравнению и граничным условиям; пусть это будут функции u₁(x,t), u₂(x,t), …, u_n(x,t)… На втором этапе строится линейная комбинация из этих функций:

u(x,t)=c₁u₁(x,t)+ c₂u₂(x,t)+…+ c_nu_n(x,t)+…

Здесь под линейной комбинацией понимается и сумма бесконечного ряда.

В силу однородности уравнения и однородности граничных условий эта сумма также удовлетворяет и уравнению и граничным условиям при любых значениях коэффициентов ряда c_i; остаётся подобрать эти коэффициенты так, чтобы функция u(x,t) удовлетворяла и начальным условиям.

Для того чтобы осуществить этот план, попытаемся найти такие решения, которые представимы в виде произведения двух функций, одна из которых зависит только от x (обозначим её X(x)), другая только от t (обозначим её T(t)):

u(x,t)= X(x)×T(t).

Если эта функция удовлетворяет уравнению колебаний, то в результате её подстановки в уравнение колебаний получим тождество:

.

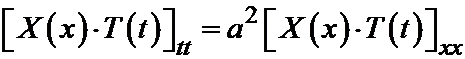Проведём дифференцирование:

.

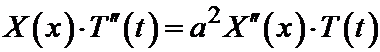Разделим переменные в этом тождестве, т.е. всё, что зависит от x переносим в одну сторону, всё что от t – в другую, получим:

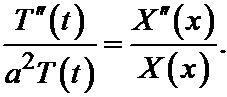
Выражения, стоящие в обеих частях не зависят ни от x, ни от t. Действительно, левая часть не зависит от x, значит и правая от x не зависит. Далее, правая часть не зависит от t; следовательно, не зависит от t и левая часть. Значит обе части равенства вообще не зависят ни от x ни от t – следовательно, они константы:

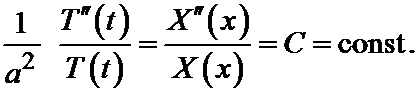
Отсюда получаем два уравнения:

.

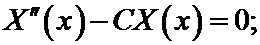
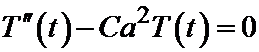Поскольку мы ищем частные решения, удовлетворяющие граничным условиям, то при любом t должны соблюдаться условия:

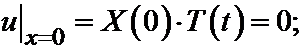
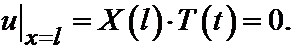
Если бы обращался в ноль второй множитель, то решение равнялось бы нулю при всех значениях x и t. Поэтому, чтобы отыскать решения, не тождественно равные нулю (а только такие решения нас и интересуют) мы должны считать, что

X(0)=0; X(l)=0.

В результате для отыскания функции X(x) мы пришли к следующей задаче. Найти решение линейного дифференциального уравнения второго порядка:

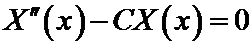
при условиях:

X(0)= X(l)=0.

Эта задача носит название задачи Штурма-Лиувилля.

Разумеется, эта задача при любом С имеет решение, тождественно равное нулю: X(x)=0. Оказывается, однако, что при некоторых значениях постоянной С, эта задача имеет и ненулевые решения.

1. Пусть 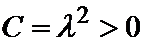. Тогда общее решение уравнения

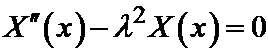
имеет вид:

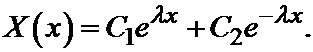
Удовлетворим это решение граничным условиям:

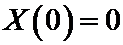
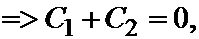
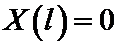
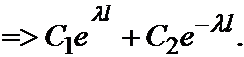
Так как определитель этой системы

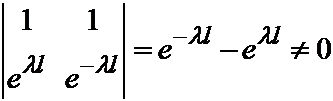
не равен нулю, то система имеет единственное решение: C₁=C₂=0.

Таким образом, в этом случае решений, отличных от тождественного нуля, не существует.

2. Пусть C=0. Тогда уравнение становится особенно простым

.

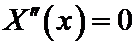Его решение – это любой полином первой степени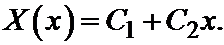

Подставляя в это решение граничные условия, имеем:

C₁=0; C₁+C₂l=0.

То есть, опять таки C₁=C₂=0.

3. Пусть, наконец C=–l²<0. Тогда уравнение будет следующим:

.

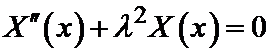Его решение имеет вид:

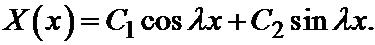
Подставляем граничные условия:

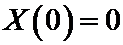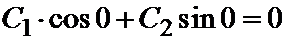=> => C₁=0,

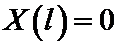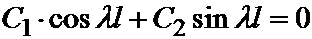=> => C₂×sinll=0.

Последнее равенство возможно, когда C₂¹0, оно будет удовлетворяться при sinll=0.

То есть при 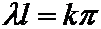(k=±1; ±2;….)

Итак, если 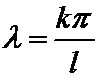, т.е. 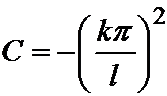, то существуют решения уравнения колебаний струны, не равные тождественно нулю.

Решение, отвечающее некоторому фиксированному k обозначим через X_k(x). Оно имеет вид:

,

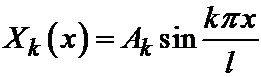где A_k – произвольная постоянная. Мы вправе в дальнейшем рассматривать только положительные значения k=1,2,…, поскольку при отрицательных k получатся решения того же вида (ведь A_k – произвольные постоянные, которые могут иметь любые знаки).

Как мы видим, каждому значению 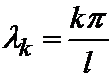соответствует бесчисленное множество решений 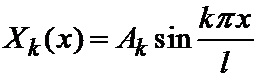, отличающихся друг от друга постоянным множителем.

Величины 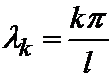называются собственными числами, а функции 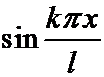– собственными функциями дифференциального уравнения 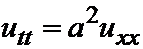с краевыми условиями 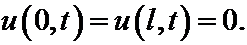Именно с такими краевыми, условиями, поскольку, как мы увидим позднее, при других краевых условиях будут другие собственные функции, а не только .

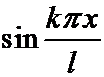Итак, задача отыскания решения уравнения

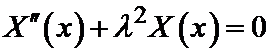
называется задачей Штурма-Лиувилля на собственные значения.

Видно, что найденные собственные функции 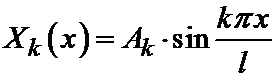– это система тригонометрических функций (в данном случае система синусов). Эта система функций ортогональна на интервале (0,l), что известно из курса анализа.

Теперь обратимся к отысканию функций T(t). Каждому собственному числу l_k будет соответствовать своя функция T_k(t), определенная уравнением

,

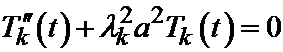или .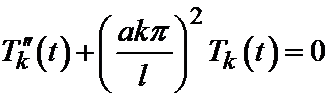

Это уравнение имеет точно такое же решение, как и уравнение

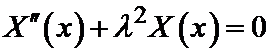, то есть

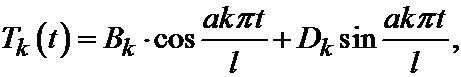
где B_k и D_k произвольные постоянные.

Подставляя найденные X_k(x) и T_k(t) в формулу 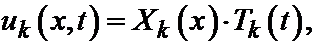получим решение:

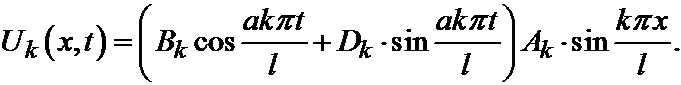Внося множитель A_k в скобку и обозначая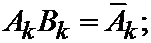 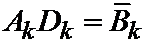запишем:

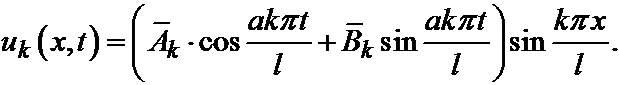
Решения u_k(x,t)называются собственными функциями задачи; соответствующие им колебания струны называются собственными колебаниями.

Сейчас осуществим вторую часть нашего плана: при помощи найденных собственных функций построим решение, удовлетворяющее начальным данным задачи.

В силу линейности и однородности уравнения колебаний струны, любая сумма решений u_k(x,t) также будет решением:

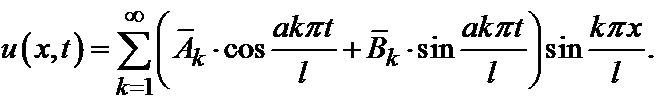
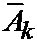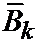Теперь будем выбирать произвольные постоянные и так, чтобы решение u(x,t) удовлетворяло первому начальному условию: .

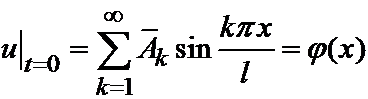Дифференцируя этот ряд по t, имеем:

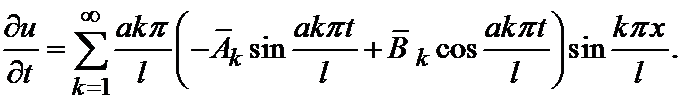
И подставляя t=0, удовлетворим решение второму начальному условию:

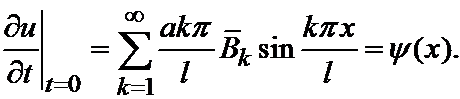
Эти формулы показывают, что величины 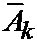и 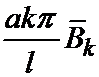являются коэффициентами Фурье разложения функций j(x) и y(x) в ряды Фурье по синусам в интервале от 0 до l (0, l).

Вспоминая формулы для этих коэффициентов, найдём (чёрточки у 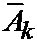и 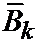опустим):

.

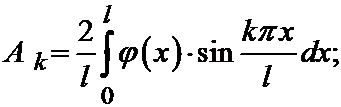
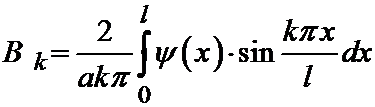Эти константы называются коэффициентами Фурье начальных данных. То есть мы получаем решение в следующем виде:

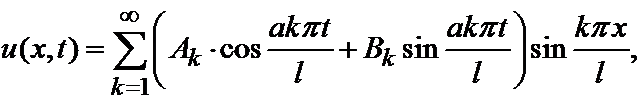
где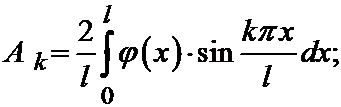

.

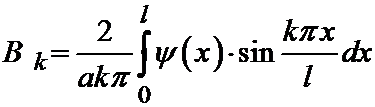коэффициенты Фурье начальных данных.