Тема 5.« Определение точек разрыва и асимптот функций»
 Определение 1. Если при нахождении предела функции выбирать значения переменной х только слева от точки хо, то такой предел называется левосторонними обозначается Определение 1. Если при нахождении предела функции выбирать значения переменной х только слева от точки хо, то такой предел называется левосторонними обозначается 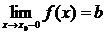 . Определение 2. Если при нахождении предела функции выбирать значения переменной х только справа от точки хо, то такой предел называется правосторонним и обозначается . Определение 2. Если при нахождении предела функции выбирать значения переменной х только справа от точки хо, то такой предел называется правосторонним и обозначается 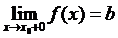 . Пример 1.Вычислите односторонние пределы функции . Пример 1.Вычислите односторонние пределы функции 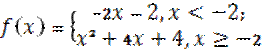 в точке в точке 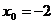 . Решение. Для нахождения левостороннего предела функции в точке . Решение. Для нахождения левостороннего предела функции в точке 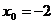 будем выбирать значения переменной, меньшие -2. Но при будем выбирать значения переменной, меньшие -2. Но при 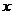 <-2 наша функция задается формулой <-2 наша функция задается формулой 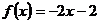 . Таким образом, получим: . Таким образом, получим: 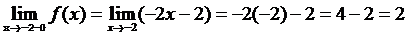 . При нахождении правостороннего предела функции в точке . При нахождении правостороннего предела функции в точке 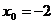 будем выбирать значения переменной, большие -2. Но при будем выбирать значения переменной, большие -2. Но при 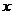 > -2 наша функция задается формулой > -2 наша функция задается формулой 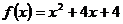 . Таким образом, получим: . Таким образом, получим: 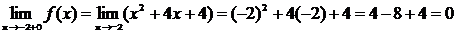 . Ответ . Ответ 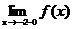 =2, =2, 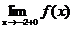 =0. Определение 3. Функция у=f(x) называется непрерывной в точке хо, если она определена в ней, существует предел функции в этой точке и он равен значению функции в этой точке, т.е. =0. Определение 3. Функция у=f(x) называется непрерывной в точке хо, если она определена в ней, существует предел функции в этой точке и он равен значению функции в этой точке, т.е.  . Определение 4. Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции. Все точки разрыва функции подразделяются на точки разрыва первого и второго рода. Определение 5. Точка разрыва хо называется точкой разрыва первого рода, если в этой точке существуют конечные левосторонние и правосторонние пределы, т.е. . Определение 4. Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции. Все точки разрыва функции подразделяются на точки разрыва первого и второго рода. Определение 5. Точка разрыва хо называется точкой разрыва первого рода, если в этой точке существуют конечные левосторонние и правосторонние пределы, т.е. 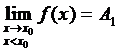 и и 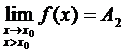 . Определение 6. Если А1 = А2, то точка хо называется точкой устранимого разрыва. Определение 7. Точка разрыва хо называется точкой разрыва второго рода, если в этой точке хотя бы один (левосторонний или правосторонний) предел не существует или равен бесконечности. Пример 2. Найдите точки разрыва и определите . Определение 6. Если А1 = А2, то точка хо называется точкой устранимого разрыва. Определение 7. Точка разрыва хо называется точкой разрыва второго рода, если в этой точке хотя бы один (левосторонний или правосторонний) предел не существует или равен бесконечности. Пример 2. Найдите точки разрыва и определите 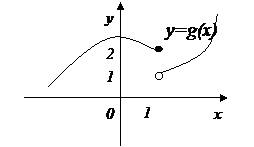 их род для функции их род для функции  , заданной графически: Решение: Непрерывность функции , заданной графически: Решение: Непрерывность функции  нарушена в единственной точке нарушена в единственной точке 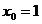 . Она будет точкой разрыва функции. Определим ее род. Для этого по графику найдем односторонние пределы функции в этой точке: . Она будет точкой разрыва функции. Определим ее род. Для этого по графику найдем односторонние пределы функции в этой точке: 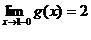 и и 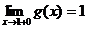 . Они существуют и конечны. Следовательно, точка . Они существуют и конечны. Следовательно, точка 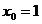 является точкой разрыва I рода функции. Поскольку односторонние пределы не равны друг другу, точка является точкой разрыва I рода функции. Поскольку односторонние пределы не равны друг другу, точка 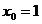 будет точкой устранимого разрыва. будет точкой устранимого разрыва. 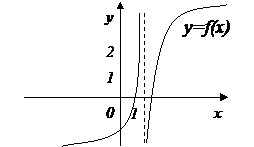 Ответ: Ответ: 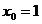 - точка разрыва функции I рода (точка устранимого разрыва). Пример 3. Найдите точки разрыва и определите их род для функции - точка разрыва функции I рода (точка устранимого разрыва). Пример 3. Найдите точки разрыва и определите их род для функции 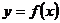 , заданной графически: Решение: Непрерывность функции , заданной графически: Решение: Непрерывность функции 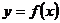 нарушена в единственной точке нарушена в единственной точке 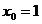 . Она будет точкой разрыва функции. Определим ее род. Для этого по графику найдем односторонние пределы функции в этой точке: . Она будет точкой разрыва функции. Определим ее род. Для этого по графику найдем односторонние пределы функции в этой точке: 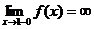 и и 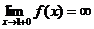 . Они существуют , и оба равны бесконечности. Следовательно, точка . Они существуют , и оба равны бесконечности. Следовательно, точка 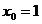 является точкой разрыва II рода функции. Ответ: является точкой разрыва II рода функции. Ответ: 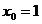 - точка разрыва функции II рода. Пример 4.Найдите точки разрыва функции у= - точка разрыва функции II рода. Пример 4.Найдите точки разрыва функции у= 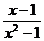 и определите их род. Решение. Функция у= и определите их род. Решение. Функция у= 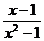 является элементарной, следовательно, она непрерывна на области определения. Найдем D(у): х2-1≠0; х≠1 и х≠-1. Получили, что точки является элементарной, следовательно, она непрерывна на области определения. Найдем D(у): х2-1≠0; х≠1 и х≠-1. Получили, что точки 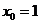 и и 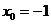 являются точками разрыва функции. Для того, чтобы их классифицировать, найдем односторонние пределы функции в указанных точках. Для точки являются точками разрыва функции. Для того, чтобы их классифицировать, найдем односторонние пределы функции в указанных точках. Для точки 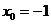 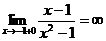 , следовательно, , следовательно, 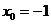 - точка разрыва II рода. Для точки - точка разрыва II рода. Для точки 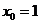 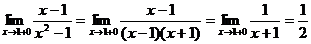 , , 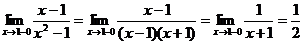 . Следовательно, . Следовательно, 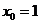 - точка разрыва I рода. Поскольку левосторонний и правосторонний пределы функции в этой точке совпадают, то - точка разрыва I рода. Поскольку левосторонний и правосторонний пределы функции в этой точке совпадают, то 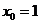 – точка устранимого разрыва. Положив у= – точка устранимого разрыва. Положив у= 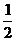 при при 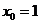 , разрыв устранится, функция станет непрерывной Ответ: , разрыв устранится, функция станет непрерывной Ответ: 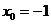 - точка разрыва функции II рода, - точка разрыва функции II рода, 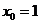 - точка разрыва функции I рода. ______________________________________________________________________ Определение 8. Прямая, к которой неограниченно приближается график функции, называется асимптотой этой функции. - точка разрыва функции I рода. ______________________________________________________________________ Определение 8. Прямая, к которой неограниченно приближается график функции, называется асимптотой этой функции.
Пример 5. Найдите асимптоты графика функции Решение: Найдём точки разрыва функции, для этого Д = 4, 1)
2) у = 0- горизонтальная асимптота. 3) Ответ: х = 3 и х = 1 – вертикальные асимптоты, у = 0 – горизонтальная асимптота. |

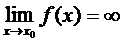 (х0 – точка разрыва)
(х0 – точка разрыва) 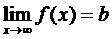
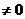 )
) 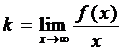
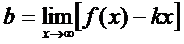
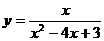
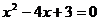 .
.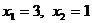
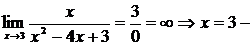 вертикальная асимптота,
вертикальная асимптота,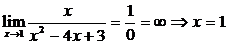 - вертикальная асимптота
- вертикальная асимптота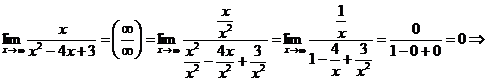 -
-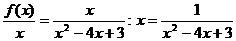 ,
, 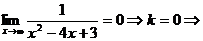 наклонных асимптот нет.
наклонных асимптот нет.