Понятие вектора. Свободный вектор

Действия с векторами. Коллинеарность векторов

В школьном курсе геометрии рассматривается ряд действий и правил с векторами:сложение по правилу треугольника, сложение по правилу параллелограмма, правило разности векторов, умножения вектора на число, скалярное произведение векторов и др.Для затравки повторим два правила, которые особенно актуальны для решения задач аналитической геометрии.

Правило сложения векторов по правилу треугольников

Рассмотрим два произвольных ненулевых вектора 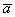и :
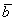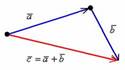
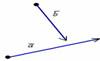Требуется найти сумму данных векторов. В силу того, что все векторы считаются свободными, отложим вектор 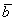от конца вектора :

Суммой векторов и 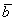является вектор 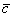. Для лучшего понимания правила в него целесообразно вложить физический смысл: пусть некоторое тело совершило путь по вектору 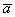, а затем по вектору 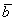. Тогда сумма векторов 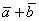представляет собой вектор результирующего пути 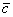с началом в точке отправления и концом в точке прибытия. Аналогичное правило формулируется для суммы любого количества векторов. Как говорится, тело может пройти свой путь сильно поддатым по зигзагу, а может и на автопилоте – по результирующему вектору суммы.

Кстати, если вектор 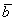отложить от начала вектора 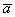, то получится эквивалентное правило параллелограмма сложения векторов.

Умножение вектора на число

Сначала о коллинеарности векторов. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Грубо говоря, речь идёт о параллельных векторах. Но применительно к ним всегда используют прилагательное «коллинеарные».

Представьте два коллинеарных вектора. Если стрелки данных векторов направлены в одинаковом направлении, то такие векторы называются сонаправленными. Если стрелки смотрят в разные стороны, то векторы будут противоположно направлены.

Обозначения: коллинеарность векторов записывают привычным значком параллельности: 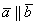, при этом возможна детализация: 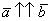(векторы сонаправлены) или 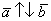(векторы направлены противоположно).

Произведением ненулевого вектора 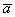на число 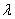является такой вектор 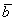, длина которого равна 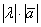, причём векторы 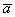и 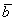сонаправлены при 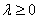и противоположно направлены при .

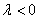Правило умножения вектора на число легче понять с помощью рисунка:

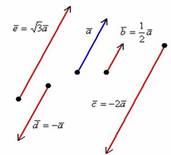
Разбираемся более детально:

1) Направление. Если множитель 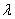отрицательный, то вектор меняет направление на противоположное.

2) Длина. Если множитель заключен в пределах 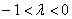или 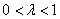, то длина векторауменьшается. Так, длина вектора 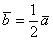в два раза меньше длины вектора 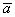. Если множитель 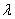по модулю больше единицы, то длина вектора увеличивается в 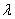раз.

3) Обратите внимание, что все векторы коллинеарны, при этом один вектор выражен через другой, например, 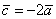. Обратное тоже справедливо: если один вектор можно выразить через другой, то такие векторы обязательно коллинеарны. Таким образом: если мы умножаем вектор на число, то получится коллинеарный (по отношению к исходному) вектор.

4) Векторы 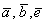сонаправлены. Векторы 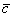и 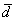также сонаправлены. Любой вектор первой группы противоположно направлен по отношению к любому вектору второй группы.

Как найти длину отрезка?

Длина, как уже отмечалось, обозначается знаком модуля.

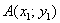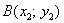Если даны две точки плоскости и , то длину отрезка 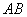можно вычислить по формуле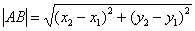

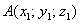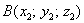Если даны две точки пространства и , то длину отрезка 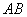можно вычислить по формуле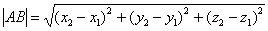

Примечание: Формулы останутся корректными, если переставить местами соответствующие координаты: 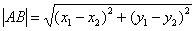и 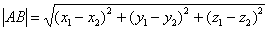, но более стандартен первый вариант

Пример 3

Даны точк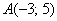и и 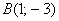. Найти длину отрезка .

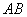Решение: по соответствующей формуле:

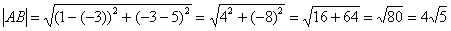
Ответ: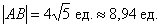

Для наглядности выполню чертёж

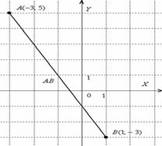
Отрезок – это не вектор, и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ 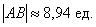можно проверить обычной линейкой, непосредственно измерив длину отрезка.

Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:

Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».

Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:

Читаем!!!

Обратите внимание на важный технический приём – вынесение множителя из-под корня. В результате вычислений у нас получился результат 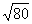и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: 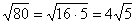. Конечно, оставить ответ в виде 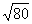не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.

Вот другие распространенные случаи:

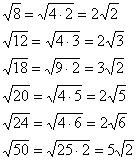
Нередко под корнем получается достаточно большое число, например 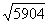. Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: 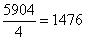. Да, разделилось нацело, таким образом: 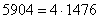. А может быть, число 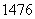ещё раз удастся разделить на 4? 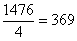. Таким образом: 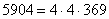. У числа 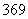последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: 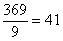. В результате:
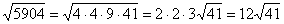Готово.

Вывод: если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.

В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.

Давайте заодно повторим возведение корней в квадрат и другие степени:

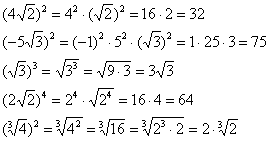
Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.

Задание для самостоятельного решения с отрезком в пространстве:

Пример 4

Даны точк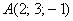и и 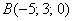. Найти длину отрезка .

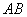Решение и ответ в конце урока.

Как найти длину вектора?

Если дан вектор плоскости 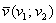, то его длина вычисляется по формуле .

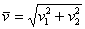Если дан вектор пространства 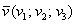, то его длина вычисляется по формуле .

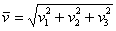Данные формулы (как и формулы длины отрезка) легко выводятся с помощью небезызвестной теоремы Пифагора.

Пример 5

Даны точк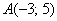и и 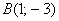. Найти длину вектора .

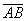Я взял те же точки, что и в Примере 3.

Решение: Сначала найдём вектор :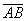

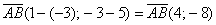
По формуле 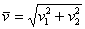вычислим длину вектора:

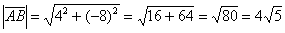
Ответ: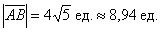

Не забываем указывать размерность – «единицы»! Всегда ли, кстати, нужно рассчитывать приближенное значение (в данном примере 8,94), если этого не требуется в условии? С моей точки зрения, лишним не будет, отсутствие приближенного значения тянет на придирку. Округление целесообразно проводить до 2-3 знаков после запятой.

Выполним чертеж к задаче:

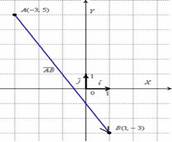
В чём принципиальное отличие от Примера 3? Отличие состоит в том, что здесь речь идёт о векторе, а не об отрезке. Вектор можно переместить в любую точку плоскости.

А в чём сходство Примера 3 и Примера 5? Геометрически очевидно, что длина отрезка 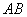равна длине вектора 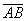. Так же очевидно, что длина вектора 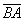будет такой же. По итогу: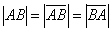

Задачу 3 можно было решить и вторым способом, повторю условие: Даны точк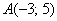и и 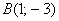. Найти длину отрезка .

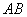Вместо применения формулы 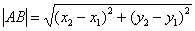, поступаем так:
1) Находим вектор .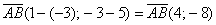
2) А теперь ссылаемся на то, что длина отрезка 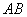равна длине вектора :

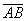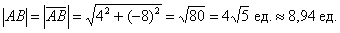
Этот способ широко практикуется в ходе решений задач аналитической геометрии.

Вышесказанное справедливо и для пространственного случая

Для тренировки:

Пример 6

а) Даны точк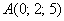и и 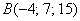. Найти длину вектора .
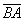б) Даны векторы 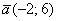, , 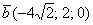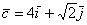и 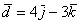. Найти их длины.

Решения и ответы в конце урока.

Понятие вектора. Свободный вектор

Сначала повторим школьное определение вектора. Вектором называется направленныйотрезок, для которого указано его начало и конец:

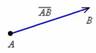
В данном случае началом отрезка является точка , концом отрезка – точка . Сам вектор обозначен через 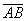. Направление имеет существенное значение, если переставить стрелку в другой конец отрезка, то получится вектор 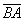, и это уже совершенно другой вектор. Понятие вектора удобно отождествлять с движением физического тела: согласитесь, зайти в двери института или выйти из дверей института – это совершенно разные вещи.

Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором 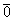. У такого вектора конец и начало совпадают.

!!! Примечание: Здесь и далее можете считать, что векторы лежат в одной плоскости или можете считать, что они расположены в пространстве – суть излагаемого материала справедлива и для плоскости и для пространства.

Обозначения: Многие сразу обратили внимание на палочку без стрелочки в обозначении 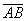и сказали, там же вверху еще стрелку ставят! Верно, можно записать со стрелкой: 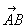, но допустима и запись 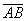, которую я буду использовать в дальнейшем. Почему? Видимо, такая привычка сложилась из практических соображений, слишком разнокалиберными и мохнатыми получались мои стрелки в школе и ВУЗе. В учебной литературе иногда вообще не заморачиваются клинописью, а выделяют буквы жирным шрифтом: 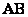, подразумевая тем самым, что это вектор.

То была стилистика, а сейчас о способах записи векторов:

1) Векторы можно записать двумя большими латинскими буквами:
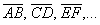и так далее. При этом первая буква обязательно обозначает точку-начало вектора, а вторая буква – точку-конец вектора.

2) Векторы также записывают маленькими латинскими буквами:
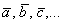В частности, наш вектор 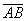можно для краткости переобозначить маленькой латинской буквой .

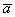Длиной или модулем ненулевого вектора 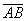называется длина отрезка 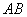. Длина нулевого вектора 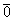равна нулю. Логично.

Длина вектора обозначается знаком модуля: ,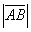

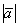
Как находить длину вектора мы узнаем (или повторим, для кого как) чуть позже.

То были элементарные сведения о векторе, знакомые всем школьникам. В аналитической же геометрии рассматривается так называемый свободный вектор.

Если совсем просто – вектор можно отложить от любой точки:

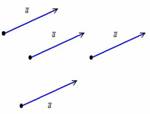
Такие векторы мы привыкли называть равными (определение равных векторов будет дано ниже), но чисто с математической точки зрения это ОДИН И ТОТ ЖЕ ВЕКТОР илисвободный вектор. Почему свободный? Потому что в ходе решения задач вы можете «пристроить» тот или иной вектор в ЛЮБУЮ, нужную вам точку плоскости или пространства. Это очень крутое свойство! Представьте вектор произвольной длины и направления – его можно «клонировать» бесконечное количество раз и в любой точке пространства, по сути, он существует ВЕЗДЕ. Есть такая студенческая присказка: Каждому лектору в ж**у по вектору. Ведь не просто остроумная рифма, всё математически корректно – вектор можно пристроить и туда. Но не спешите радоваться, чаще страдают сами студенты =)

Итак, свободный вектор – это множество одинаковых направленных отрезков. Школьное определение вектора, данное в начале параграфа: «Вектором называется направленный отрезок…», подразумевает конкретный направленный отрезок, взятый из данного множества, который привязан к определённой точке плоскости или пространства.

Следует отметить, что с точки зрения физики понятие свободного вектора в общем случае некорректно, и точка приложения вектора имеет значение. Действительно, прямой удар одинаковой силы по носу или по лбу хватит развивать мой дурацкий пример влёчет разные последствия.

Далее, если не оговаривается иное, речь пойдёт только о свободных векторах.