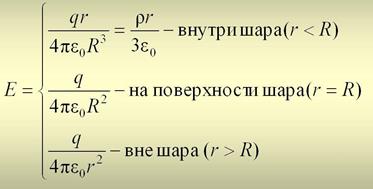Поток вектора напряженности электрического поля. Теорема Остроградского-Гаусса. Понятие дивергенции вектора. Математический оператор набла

Лекция 2

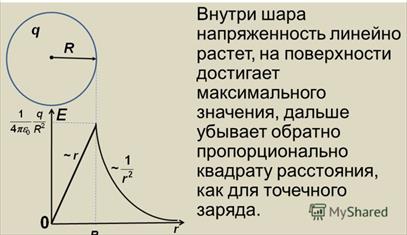
Расчет электрических полей. Понятие дивергенции вектора. Теорема Остроградского-Гаусса. Распределение зарядов: линейное, поверхностное, объемное. Основной закон электростатики – закон Гаусса. Примеры применения закона Гаусса: сферическая оболочка, шар, бесконечная плоскость, цилиндрическая поверхность, бесконечная прямая нить.

Способ 1.Применение принципа суперпозиции для нахождения напряжённости поля системы зарядов и протяжённых заряженных тел

Этот способ принципиально применим всегда. Другое дело, что получить

точный результат аналитически, без применения численных

методов и ЭВМ, удаётся только в очень ограниченном ряде случаев распределения зарядов-источников в пространстве.

Пример .Определить напряженность на оси равномерно заряженного кольца. Заряд кольца q, x – расстояние от центра кольца.

Прежде всего разобьём кольцо на элементы – точечные

заряды Δqi, каждый из которых создаёт в точке А поле с напряженнстью

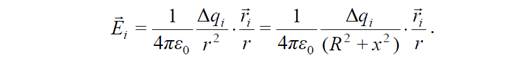
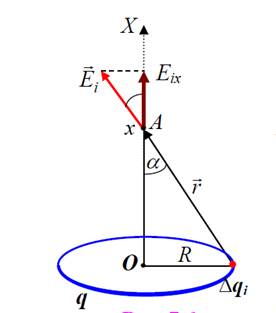
Расстояние от элемента Δqi, кольца до точки А одинаково для всех таких элементов. Все векторы располагаются под одинаковым углом к оси

ОХ на конической поверхности. Далее воспользуемся принципом

суперпозиции, т.е. сложим все такие векторы. Вследствие симметрии задачи вклад в общую напряжённость дадут лишь составляющие Е_xi. Поэтому

модуль вектора напряжённости в точке А будет равен только сумме именно этих составляющих Еix от всех элементов кольца:

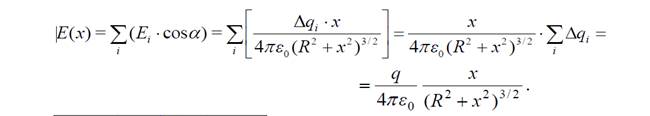
Сам же вектор Е очевидно, будет направлен вдоль оси ОХ.

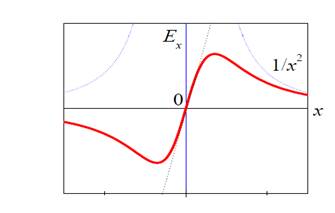
Рис.2. Зависимость проекции на ось ОХ вектора напряжённости Ex .

Видно, что на малых расстояниях от центра кольца эта

зависимость линейная, на больших – обратно пропорциональная

квадрату расстояния (кольцо “становится” точечным зарядом).

Чаще такие задачи решают, используя процедуру интегрирования.

Пример на доске. При этом полагают, что заряд распределен непрерывно по телу.

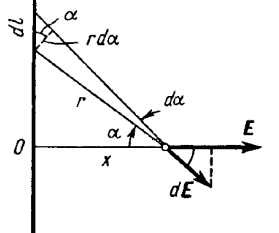
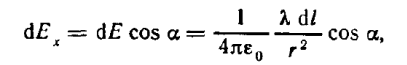
Надо привести уравнение к одной переменной. Выберем угол альфа.

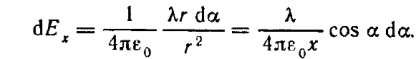
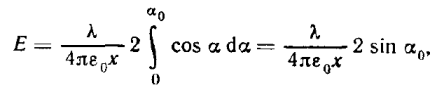
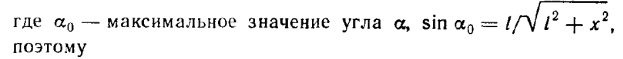
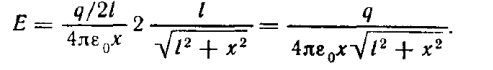
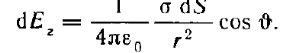
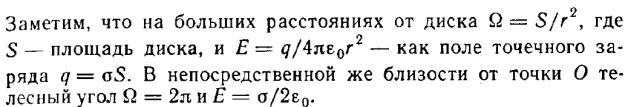
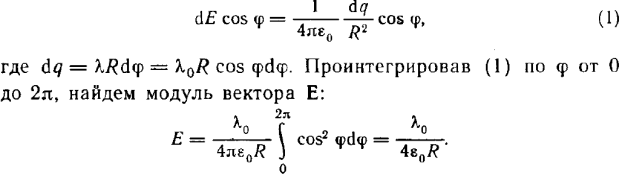
Поток вектора напряженности электрического поля. Теорема Остроградского-Гаусса. Понятие дивергенции вектора. Математический оператор набла.

Многое задачи электростатики решаются намного изящнее и проще, если использовать такие свойства векторного поля, как теоремаОстроградского-Гаусса и теорема о циркуляции вектора. Эти свойства связаны с такими математическими понятиями как поток вектора, циркуляция и дивергенция вектора.

Элементарным потоком напряженности электрического поля dФ через произвольную площадку dS называют произведение модуля вектора Ена dS и на косинус угла α между вектором напряженности электрического поля и положительной нормалью к площадке.

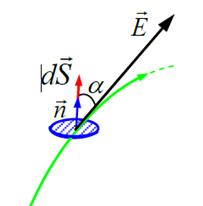dФ = Е ∙dS∙cosα или dФ = (Е ∙ dS)

Полный поток через замкнутую поверхность будет равен интегралу по поверхности по элементарным потокам.

Ф = = 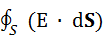или

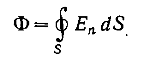Если соблюдено условие – густота силовых линий пропорциональна модулю напряжённости поля, то справедливо и следующее важное утверждение: поток вектора напряжённости через данную поверхность пропорционален числу силовых линий проходящих сквозь неё.

Нужно сделать важную оговорку: поскольку

поток «величина алгебраическая», т.е. может иметь

разный знак в зависимости от

направления, в котором силовые линии пересекают поверхность (знака скалярного произведения EndS или соответствующей суммы), договоримся и «число линий» считать с учётом этого направления. Договоримся также, при этом, для замкнутых поверхностей положительными считать нормали n смотрящие вовне. Тогда линия «выходящая» изнутри наружу даёт вклад «+1», а «входящая» снаружи вовнутрь – «-1»

Теорема Остроградского-Гаусса.

Поток вектора напряжённости электростатического поля

Ф в вакууме через любую замкнутую поверхность пропорционален суммарному заряду, расположенному внутри этой поверхности ,деленному на электрическую постоянную

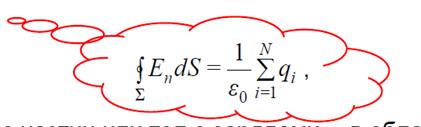
Физический смысл. Поток вектора Е через поверхность численно равен числу силовых линий пронизывающих эту поверхность.

Проведём теперь доказательство утверждения теоремы «по

шагам», отталкиваясь от самого простого случая:

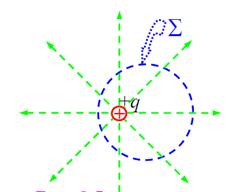
а) сферическая поверхность охватывает точечный

положительный заряд*), расположенный в её центре

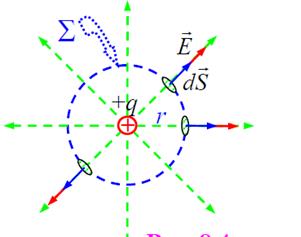
Рассчитаем поток вектора

напряжённости. Структура поля

точечного заряда нам уже хорошо

известна – в любой точке пространства

вектор напряжённости имеет радиальное

направление, а его величина обратно пропорциональна квадрату расстояния от точечного заряда-источника поля. Отметим, прежде всего, то, что для любого малого элемента сферической поверхности направления векторов E

и dS совпадают. Это позволяет перейти от проекции

вектора E_n к его модулю E(r) под знаком интеграла (мы добавили

в обозначении модуля напряжённости указание на то, что

имеется зависимость только от расстояния!):

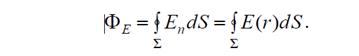
Далее подставим известное нам выражение для напряжённости

поля точечного заряда:

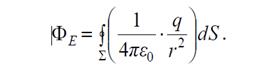
Подынтегральное выражение в скобках есть константа в пределах всей

поверхности интегрирования S, поэтому её можно вынести за

знак интеграла. Оставшийся интеграл в строгом соответствии с

математическим определением не что иное, как площадь

поверхности S, равная для сферы, как известно, 4πr².

В итоге получаем для искомого потока результат:

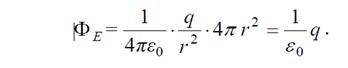Как видим, он вполне соответствует утверждению теоремы.

б) сместим точечный заряд из центра всё той же

сферической поверхности

Обратим внимание, что вычисление

поверхностного интеграла (потока) в этом

случае сразу существенно усложняется.

Ведь теперь для каждого малого элемента

поверхности угол между векторами Eи dS

разный, также как разные значения принимает модуль напряженности.

Рисунок помогает понять, что обсуждаемый поток ничуть не изменяется

по сравнению со случаем «а». Вспомним, что поток через

поверхность пропорционален числу силовых линий пересекающих

эту поверхность. Это число, очевидно, не изменилось при

смещении заряда из центра. Поэтому можно предполагать, что остаётся в силе и утверждение теоремы Гаусса.

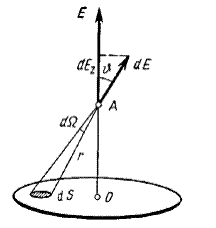
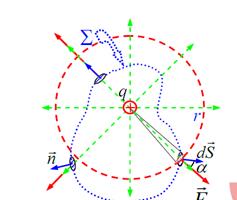Вычислим поток через произвольную поверхность математически строго, используя dФ = Е ∙dS∙cosα.

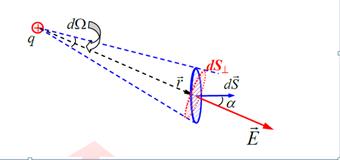
Как видно из рисунка dS∙cosα = dS_┴

Учитывая , что телесный угол dΩ = dS_┴/r² для точечного заряда запишем.

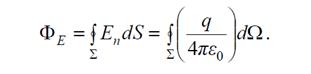
Выражение в скобках под знаком интеграла, очевидно, постоянная

величина, а телесный угол при обходе всей замкнутой

поверхности, охватывающей точечный заряд, изменяется в

пределах от 0 до 4π. Учитывая это, приходим к уже знакомому выражению

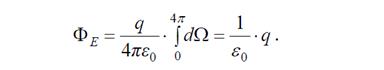
в) замкнутая поверхность произвольной формы охватывает

один точечный заряд. Морщинистая поверхность.

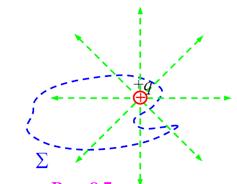
видно, что число силовых линий «истекающих» через поверхность ∑ наружу не изменилось (напомним, что мы выбрали случай положительного

заряда).Оно не изменяется даже в случае самых причудливых, например,

«складчатых» замкнутых поверхностей, охватывающих точечный заряд. Несмотря на то, что в последнем

случае, силовая линия может пересекать поверхность несколько раз, её итоговый «вклад» всегда равен «+1».

Проследите по рисунку, что число «выходов» всегда на единицу

превышает число «входов». Таким образом, и в этом случае

поток пропорционален заряду q внутри поверхности S.

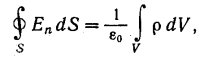
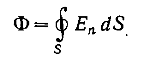
Пример 1. Поле равномерно заряженной бесконечной плоскости.

Плоскость равномерно заряжена с постоянной поверхностной плотностью заряда s.

В качестве замкнутой поверхности построим цилиндр основания которого ½½плоскости, а ось ^ ей.

Поток Есквозь боковую поверхность =0, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания.

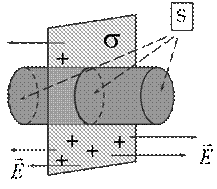
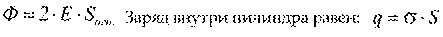
Вывод: напряженность не зависит от длины цилиндра т.е. Напряженность поля на любых расстояниях от плоскости одинакова, следовательно поле заряженной плоскости однородно.

Пример 2.Поле бесконечной однородно заряженной нити с линейной плотностью τ ( τ = dq/dl, Кл/м).

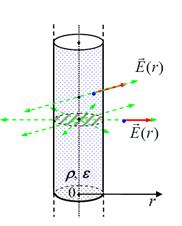
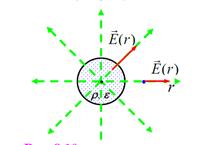
Поле симметричное, направлено перпендикулярно нити и из соображений симметрии на одинаковом расстоянии от оси симметрии цилиндра (нити) имеет одинаковое значение.

Модуль напряжённости может зависеть от расстояния от оси стержня r, но никак не от азимутального направления.

Критерий выбора замкнутой поверхности

На части этой поверхности вектор E должен совпадать с

направлением нормали и быть постоянным по модулю, а на

оставшейся части перпендикулярным к ней.

Этому критерию удовлетворят поверхность прямого кругового цилиндр

Процедура «вычисления» поверхностного интеграла вида

ò E_n dS может быть записана

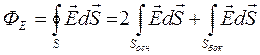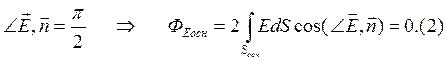Для оснований цилиндра

Для боковой поверхности

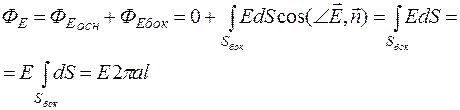
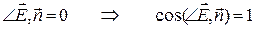Тогда найдем поток вектора магнитной индукции по определению потока

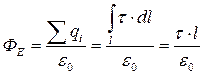Найдем поток вектора магнитной индукции по теореме Гаусса

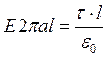Приравняем оба выражения

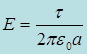и найдем Е:

Здесь а радиус основания цилиндра, окружающего нить, т.е.расстояние от нити до данной точки пространства, τ(тау) - поверхностная плотность заряда.

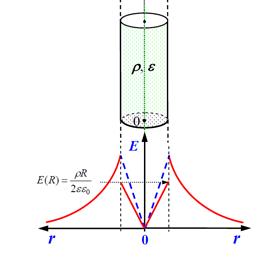
Пример 3.Электрическое поле вне и внутри объемно заряженного бесконечного цилиндра радиуса R.

Распределение заряда так же, как и в случае с нитью имеет «аксиальную» (относительно оси) симметрию. Графическое изображение силового поля так же аналогично, изображению поля нити. Легко понять, что поле вне цилиндра будет аналогично полю нити.

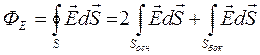
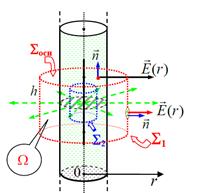Поток напряженности электрического поля через основания цилиндра равен нулю, т.к. угол между нормалью и вектором Е равен 90⁰.Тогда

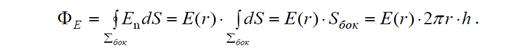
Таким образом, поверхностный интеграл удалось представить в

виде произведения скалярных величин. По внешнему виду он

выглядит совершенно одинаково как для поверхности S₁

(охватывающей часть стержня снаружи), так и для поверхности S₂

(расположенной внутри стержня). Разница здесь лишь в принадлежности r к определённому диапазону значений радиуса: r > R и r < R для S₁ и S₂

Отличие для поверхностей S1 и S2 обнаруживается в

величине охваченного ими заряда:

а)В первом случае (r > R) поверхность s1 охватывает весь

заряд участка стержня длины h. При постоянной объёмной

плотности заряда r получаем:

q₁ = 2×p R ×hr

(2×p R ×h – объём прямого кругового цилиндра высоты h).

б)Цилиндрическая поверхность S2 имеет радиус r меньший,

чем у стержня, и охватывает лишь часть заряда распределённого

внутри участка стержня высоты h. Этот заряд равен

q₂ = 2×p r hr

Тогда по теореме Гаусса поток напряженности электрического поля вне цилиндра будет равен: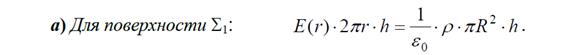

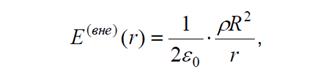при r > R (поле вне стержня).

Итак, вне стержня поле имеет радиальное направление и убывает обратно пропорционально расстоянию от оси заряженного цилиндра.

б) Для поверхности S2

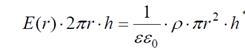
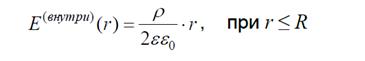
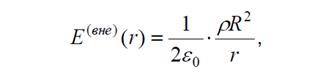
Ключевым моментом в проведённых решениях являлся переход от поверхностного интеграла от (E dS) , представляющего собой в общем случае весьма сложную с математической точки зрения конструкцию, к произведению скалярных величин вида Е×S. Такой переход возможен только при наличии одного из трёх видов

симметрии распределения заряда в пространстве – сферической,

осевой («аксиальной») или плоской («билатеральной» или

«зеркальной»)*). При произвольной форме заряженного тела единственно возможным остаётся лишь «первый» способ

расчёта напряжённости, основанный на непосредственном

применении принципа суперпозиции электрических полей, или её

экспериментальное измерение.

Пример 3. Поле полого шара. (Поле проводящего шара)

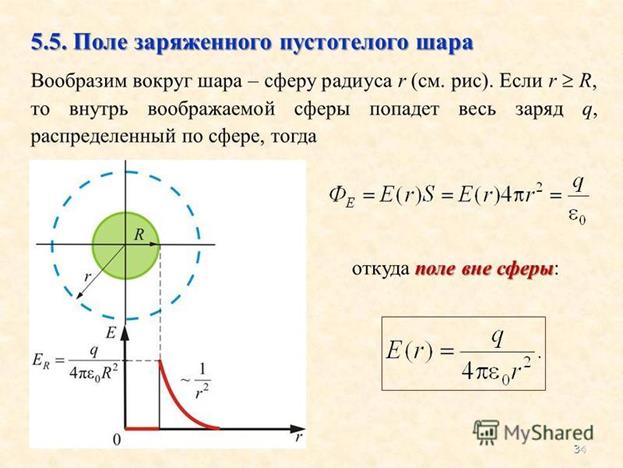
Внутри шара электрическое поле отсутствует. На этом явлении основана электростатическая защита.

Пример 4. Поле равномерно заряженного шара. Заряд шара q, радиус R.