Разложение функции в ряды Тейлора.
Ряд Тейлора — разложение функции в бесконечную сумму степенных функций.
Ряд назван в честь английского математика Брука Тейлора, хотя ряд Тейлора был известен задолго до публикаций Тейлора — его использовали ещё в XVII веке Грегори, а также Ньютон.
Ряды Тейлора применяются при аппроксимации функции многочленами. В частности, линеаризация уравнений происходит путёмразложения в ряд Тейлора и отсечения всех членов выше первого порядка.
Определение:
Пусть функция 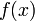 бесконечно дифференцируема в некоторой окрестности точки
бесконечно дифференцируема в некоторой окрестности точки 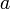 . Формальный ряд
. Формальный ряд
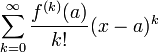
называется рядом Тейлора функции 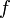 в точке
в точке 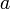 .
.
Связанные определения:
В случае, если 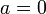 , этот ряд также называется рядом Макло́рена.
, этот ряд также называется рядом Макло́рена.
Свойства
Если 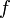 есть аналитическая функция в любой точке a, то её ряд Тейлора в любой точке
есть аналитическая функция в любой точке a, то её ряд Тейлора в любой точке 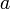 области определения
области определения 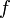 сходится к
сходится к 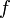 в некоторой окрестности
в некоторой окрестности 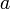 .
.
Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности 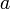 . Например, Коши предложил такой пример:
. Например, Коши предложил такой пример:
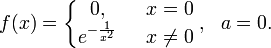
У этой функции все производные в нуле равны нулю, поэтому коэффициенты ряда Тейлора в точке 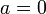 равны нулю.
равны нулю.
Формула Тейлора
Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.
Теорема:
Пусть функция 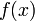 имеет имеет 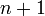 производную в некоторой окрестности точки производную в некоторой окрестности точки 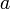 , , 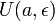 Пусть Пусть 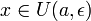 Пусть Пусть 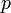 — произвольное положительное число, тогда: — произвольное положительное число, тогда: 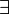 точка точка 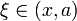 при при 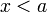 или или 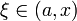 при при 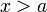 : : 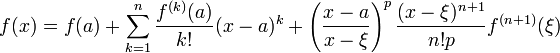 |
Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).
Разложение функции в ряд Маклорена.
Векторные и скалярные величины. Правило сложения и вычитания векторов.
Умножение вектора на число.
Умножение вектора на число
Произведением ненулевого вектора а на число х =/= 0 называется вектор, длина которого равна | x | • | а |, а направление совпадает с направлением а, если х > 0, и противоположно ему, если х < 0.
Произведением нулевого вектора на любое число х и произведением любого вектора на число нуль называется нулевой вектор.
Произведение вектора а на число х обозначается х • а (числовой множитель пишется слева).
Согласно определению | x • а | = | x | • | а | для любого вектора а и любого числа х.
На рис. 18 изображены произведения вектора а на число х = 2 (вектор CD>) и на число х = —2 (вектор EF>).
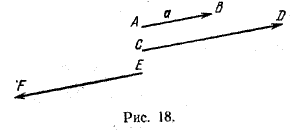
Умножение вектора на число обладает следующими свойствами:
1. Свойство ассоциативности (сочетательности):
х • (у • а) = (х • у) • а.
2. Свойство дистрибутивности (распределительности) относительно векторного множителя:
х • а + y • а = (х + у) • а.
3. Свойство дистрибутивности (распределительности) относительно числового множителя:
х • а + х • b = х • (a + b).
Если a = 0 или ху = 0, то равенство х(уа) = = (ху)а очевидно, так как слева и справа стоят нулевые векторы.
Пусть а =/= 0, ху =/= 0 и а = OA>. Тогда векторы х (у • OA>) и (ху) OA> лежат на прямой OA>, имеют длину |x| • |y| • |OA>| и направлены в одну сторону: в сторону вектора а = OA>, если ху > 0, и в противоположную сторону, если ху < 0. Таким образом, свойство 1 доказано.
Свойства 2 и 3 доказывать не будем. Заметим лишь, что свойства 1 и 2 являются свойствами векторов на прямой. Они уже доказывались в курсе геометрии восьмилетней школы. Свойство 3 является свойством векторов на плоскости; оно тоже было доказано.
Задача. В параллелограмме ABCD точка М есть точка пересечения диагоналей. Найти множитель k в каждом из следующих случаев:
1) M C> = k • CA>; 2) BD> = k • BM>; 3) AC> = k • CM>;
4) BB> = k • BD>; 5) AA> = k • CC>.
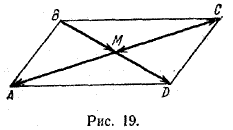
В соответствии с определением умножения вектора на число имеем (рис. 19)
1) M C> 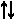 CA> , | CA| = 2•| MC |, откуда k = — 1/2;
CA> , | CA| = 2•| MC |, откуда k = — 1/2;
2) BM> 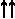 BD>, | BD | = 2 • | ВМ |, откуда k = 2;
BD>, | BD | = 2 • | ВМ |, откуда k = 2;
3) CM> 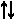 AC>, | CM | = 1/2• |AС |, откуда k = -2;
AC>, | CM | = 1/2• |AС |, откуда k = -2;
4) BB> = 0, BD> =/= 0, откуда k = 0;
5) AA> = 0, CC> = 0, откуда k — любое число.
