ВОПРОС№31: Формула Тейлора. Разложение некоторых элементарных функций по формуле Тейлора.

Теорема Тейлора. 1) Пусть функция f(x) имеет в точке х = а и некоторой ее окрестности производные порядка до (n+1) включительно.{ Т.е. и все предыдущие до порядка n функции и их производные непрерывны и дифференцируемы в этой окрестности}.

2) Пусть х- любое значение из этой окрестности, но х ¹ а.

Тогда между точками х и а найдется такая точка e, что справедлива формула(формула Тейлора):

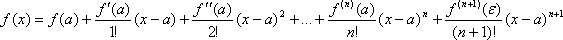
выражение: 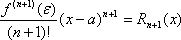называется остаточным членом в форме Лагранжа.

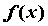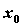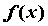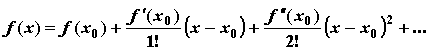
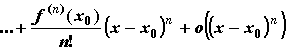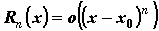Пусть функция имеет в точке производные всех порядков до n-го включительно. Тогда для справедлива формула Тейлора: ,где , называется остаточным членом формулы Тейлора в форме Пеано; 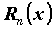— бесконечно малая более высокого порядка малости, чем .

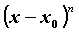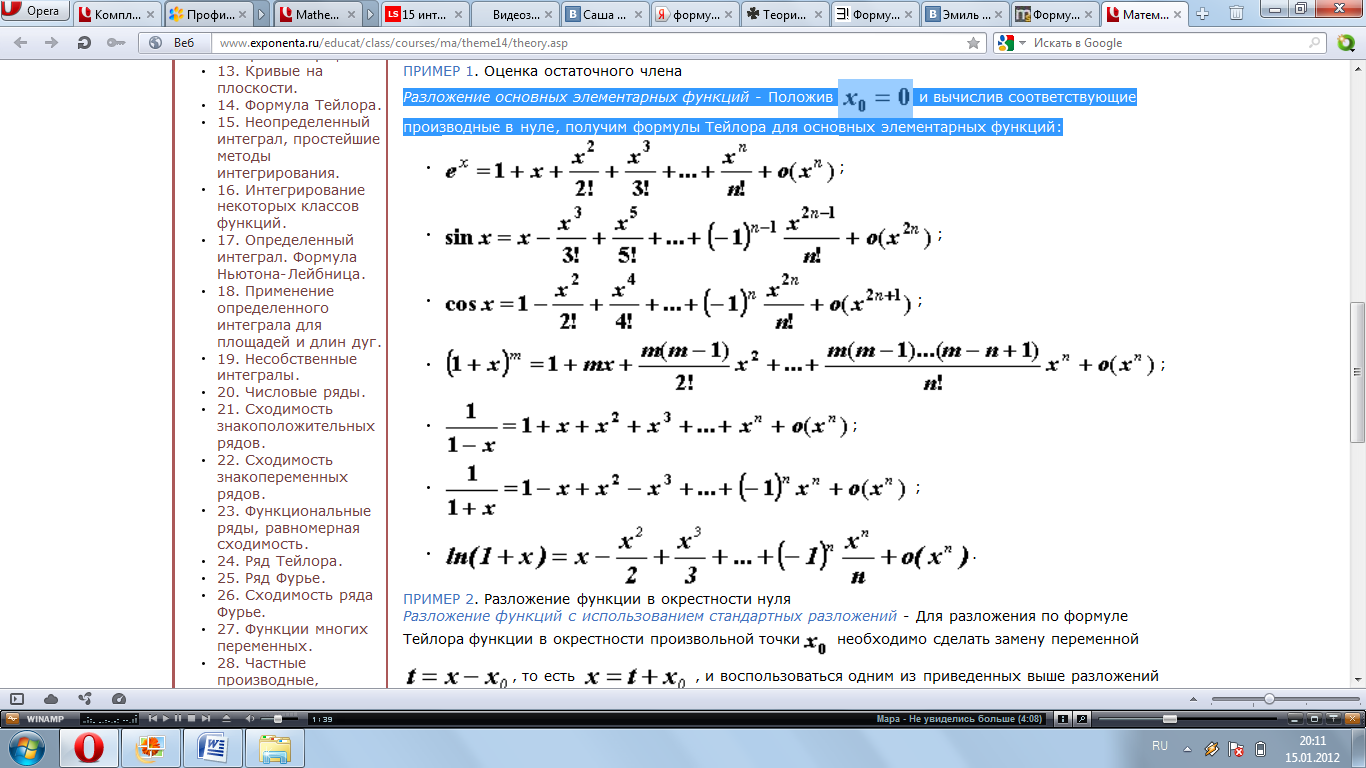
Разложение основных элементарных функций - Положив 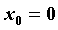и вычислив соответствующие производные в нуле, получим формулы Тейлора для основных элементарных функций:

ВОПРОС№33: основные свойства неопределенного интеграла:

1) Производная неопределенного интеграла равна подынтегральной функции. Дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е. (∫f(x)dx)′=f(x) d∫f(x)dx=f(x)dx

Доказательство:

∫f(x)dx=F(x)+C,

(∫f(x)dx)′=(F(x)+C)′=F′(x)+0=F′(x)=f(x),

d∫f(x)dx=(∫f(x)dx)′dx=f(x)dx

2) Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е. ∫dF(x)dx=F(x)+C.

Доказательство:

dF(x)=F′(x)dx=f(x)dx,

∫dF(x)dx=∫f(x)dx=F(x)+C.

3) Постоянный множитель можно выносить из под знака интеграла, т.е. ∫kf(x)dx=k∫f(x)dx,k(не равно) 0

Доказательство: Пусть F(x) -- первообразная для функции f(x), тогда

kF(x) -- первообразная для функции kf(x).

(kF(x))′=0+kF′(x)=kF′(x)=kf(x).

Таким образом

∫kf(x)dx=kF(x)+C=k(F(x)+C/k)=k(F(x)+C1)=k∫f(x)dx

4) Неопределенный интеграл от суммы(разности) двух функций равен сумме(разности) интегралов этих функций.

∫[f(x)±g(x)]dx=∫f(x)dx±∫g(x)dx

Распространяется на n слагаемых.

Доказательство:

d[∫f(x)dx±∫g(x)dx]=d∫f(x)dx±d∫g(x)dx=

=f(x)dx±g(x)dx=[f(x)±g(x)]dx.

ВОПРОС№34: Методы интегрирования.

Непосредственное интегрирование.

Пример.Найдите множество первообразных функции .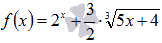
Решение.Запишем функцию в виде .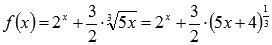
Так как интеграл суммы функций равен сумме интегралов, то

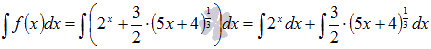
Числовой коэффициент можно вынести за знак интеграла:

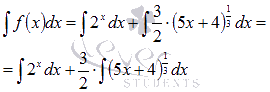
Первый из интегралов приведен к табличному виду, поэтому из таблицы первообразных для показательной функции имеем .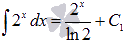
Для нахождения второго интеграла 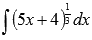воспользуемся таблицей первообразных для степенной функции 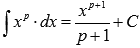и правилом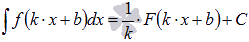
То есть, 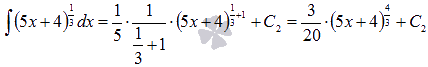. Следовательно,

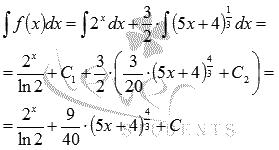
где.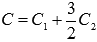

Интегрирование по частям.

Интегрирование по частям основано на представлении подынтегрального выражения в виде произведения 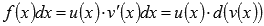и последующем применении формулы 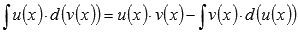. Этот метод является очень мощным инструментом интегрирования. В зависимости от подынтегральной функции, метод интегрирования по частям иногда приходится применять несколько раз подряд до получения результата. Для примера найдем множество первообразных функции арктангенс.
Пример.Вычислить неопределенный интеграл .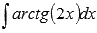
Решение.Пусть 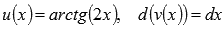, тогда

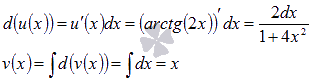
Следует отметить, что при нахождении функции v(x) не прибавляют произвольную постоянную С.
Теперь применяем формулу интегрирования по частям:

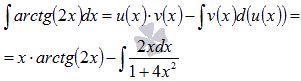
Последний интеграл вычислим по методу подведения под знак дифференциала.
Так как 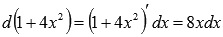, то 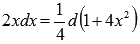. Поэтому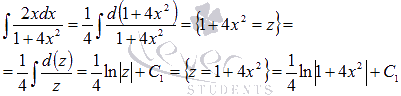
Следовательно,

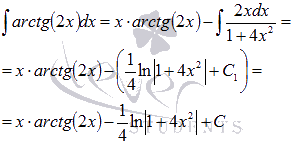
где 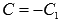. Ответ: .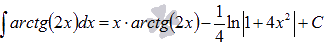