Функциональные ряды. Степенные ряды.
| Определение степенного ряда | Функциональный ряд вида 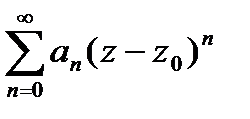 называется степенным рядом, где называется степенным рядом, где 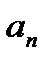 – вещественные или комплексные числа, не зависящие от – вещественные или комплексные числа, не зависящие от 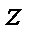 , называются коэффициентами степенного ряда; , называются коэффициентами степенного ряда; 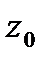 – фиксированное число, называется центром сходимости степенного ряда. Если – фиксированное число, называется центром сходимости степенного ряда. Если 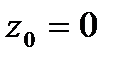 , то степенной ряд имеет вид , то степенной ряд имеет вид 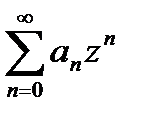 . . . . |
| Определение функционального ряда | Пусть в области Δ вещественных или комплексных чисел дана последовательность функций 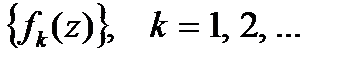 . Функциональным рядом называется сумма всех членов функциональной последовательности: . Функциональным рядом называется сумма всех членов функциональной последовательности: 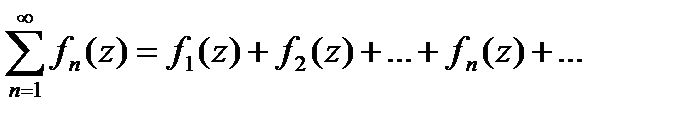 . . |
Сходимость степенного ряда.
Сходимость степенных рядов
Из формального степенного ряда с вещественными или комплексными коэффициентами путем приписывания формальной переменной 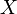 какого-нибудь значения в поле вещественных или комплексных чисел можно получить числовой ряд. Числовой ряд считается сходящимся (суммируемым), если сходится последовательность частичных сумм, составленных из его членов, и называется абсолютно сходящимся, если сходится последовательность частичных сумм, составленных из его членов, взятых по модулю (по норме).
какого-нибудь значения в поле вещественных или комплексных чисел можно получить числовой ряд. Числовой ряд считается сходящимся (суммируемым), если сходится последовательность частичных сумм, составленных из его членов, и называется абсолютно сходящимся, если сходится последовательность частичных сумм, составленных из его членов, взятых по модулю (по норме).
Признаки сходимости
Для степенных рядов есть несколько теорем, описывающих условия и характер их сходимости.
Первая теорема Абеля: Пусть ряд 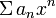 сходится в точке
сходится в точке 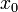 . Тогда этот ряд сходится абсолютно в круге
. Тогда этот ряд сходится абсолютно в круге 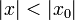 и равномерно по
и равномерно по 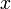 на любом компактном подмножестве этого круга.
на любом компактном подмножестве этого круга.
Обращая эту теорему, получаем, что если степенной ряд расходится при 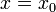 , он расходится при всех
, он расходится при всех 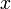 , таких что
, таких что 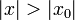 . Из первой теоремы Абеля также следует, что существует такой радиус круга
. Из первой теоремы Абеля также следует, что существует такой радиус круга 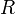 (возможно, нулевой или бесконечный), что при
(возможно, нулевой или бесконечный), что при 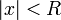 ряд сходится абсолютно (и равномерно по
ряд сходится абсолютно (и равномерно по  на компактных подмножествах круга
на компактных подмножествах круга 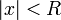 ), а при
), а при 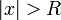 — расходится. Это значение
— расходится. Это значение 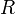 называется радиусом сходимости ряда, а круг
называется радиусом сходимости ряда, а круг 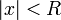 — кругом сходимости.
— кругом сходимости.
Формула Коши-Адамара: Значение радиуса сходимости степенного ряда может быть вычислено по формуле:
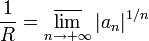
(По поводу определения верхнего предела 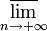 см. статью «Частичный предел последовательности».)
см. статью «Частичный предел последовательности».)
Пусть 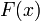 и
и 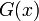 — два степенных ряда с радиусами сходимости
— два степенных ряда с радиусами сходимости 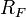 и
и 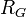 . Тогда
. Тогда
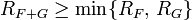
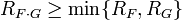
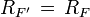
Если у ряда 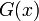 свободный член нулевой, тогда
свободный член нулевой, тогда
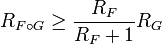
Вопрос о сходимости ряда в точках границы 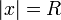 круга сходимости достаточно сложен и общего ответа здесь нет. Вот некоторые из теорем о сходимости ряда в граничных точках круга сходимости:
круга сходимости достаточно сложен и общего ответа здесь нет. Вот некоторые из теорем о сходимости ряда в граничных точках круга сходимости:
Признак Д’Аламбера: Если при 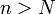 и
и 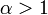 выполнено неравенство
выполнено неравенство
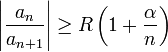
тогда степенной ряд 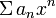 сходится во всех точках окружности
сходится во всех точках окружности 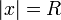 абсолютно и равномерно по
абсолютно и равномерно по 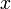 .
.
Признак Дирихле: Если все коэффициенты степенного ряда 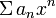 положительны и последовательность
положительны и последовательность 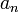 монотонно сходится к нулю, тогда этот ряд сходится во всех точках окружности
монотонно сходится к нулю, тогда этот ряд сходится во всех точках окружности 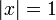 , кроме, быть может, точки
, кроме, быть может, точки 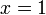 .
.
Вторая теорема Абеля: Пусть степенной ряд сходится в точке 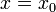 . Тогда он сходится равномерно по
. Тогда он сходится равномерно по 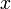 на отрезке, соединяющем точки 0 и
на отрезке, соединяющем точки 0 и 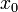 .
.
Сумма степенного ряда как функция комплексного параметра 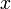 является предметом изучения теории аналитических функций.
является предметом изучения теории аналитических функций.
