Метод Даламбера для задачи о колебаниях неограниченной струны

Найти функцию 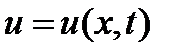, удовлетворяющую уравнению и начальным условиям (задача Коши):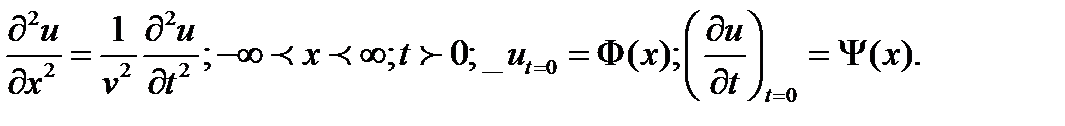

Общий интеграл уравнения имеет вид ;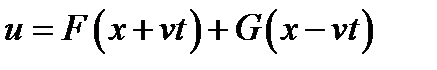

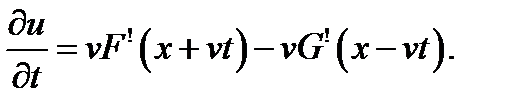
При 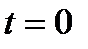будем иметь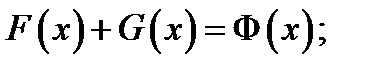

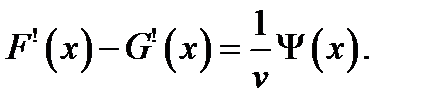
Откуда находим 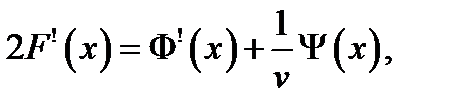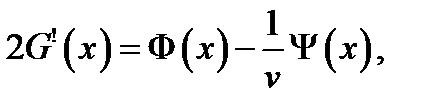или

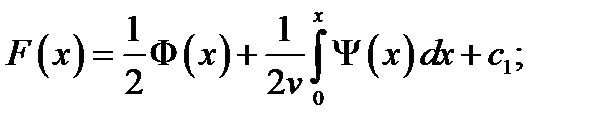
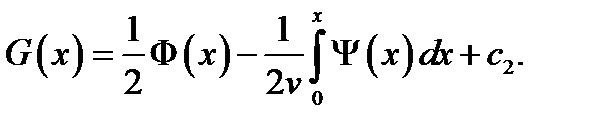
После подстановки в выражение для 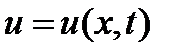получим:

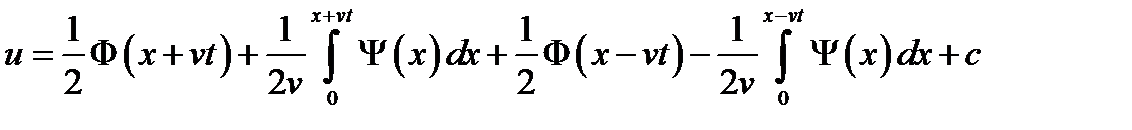, где .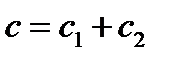

Легко видеть, что 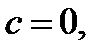это следует из начальных условий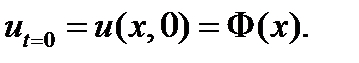

В итоге получаем формулу, называемую формулой Даламбера:

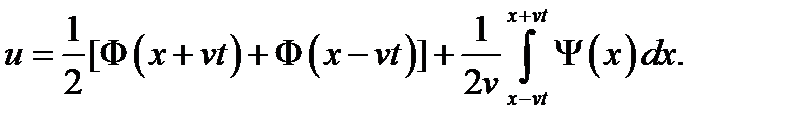
Раздел 3. Метод Фурье

3.1. Уравнения с разделяющимися переменными.

3.2. Задача Дирихле для круга. Интеграл Пуассона.

3.3. Задача Штурма-Лиувилля.

3.4. Фундаментальная система решений задачи Штурма-Лиувилля. Разложение в ряд по собственным функциям.

3.5. Метод Фурье для случая двух переменных.

Формула Грина. Теорема о среднем, принцип максимума. Функция Грина и ее применение к решение краевых задач.

Фу́нкция Гри́на используется для решения неоднородных дифференциальных уравнений с граничными условиями (неоднородной краевой задачи). Названа в честь английского математика Джорджа Грина (англ. George Green), который первым развил соответствующую теорию в 1830-х гг.

Функции Грина полезны в электростатике — для решения уравнения Пуассона; в теории конденсированных сред — они позволяют решить уравнение диффузии (и совпадающее с ним уравнение теплопроводности); в квантовой механике — функция Грина гамильтониана является одной из ключевых функций и связана с плотностью состояний. Функции Грина, используемые в этих областях, очень похожи, поскольку уравнения диффузии и уравнение Шрёдингера в некотором смысле подобны. Все области математической и теоретической физики, где крайне полезны функции Грина, пожалуй, трудно даже перечислить. Они помогают находить стационарные и нестационарные решения, в том числе при разнообразных граничных условиях.

Функция Грина G(x, s) линейного дифференциального оператора L = L(x), действующего на обобщённых функциях на подмножестве евклидового пространства Rⁿ в точке s — это любое решение уравнения

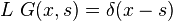где 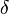— это дельта-функция Дирака. Это свойство функции Грина может использоваться для решения дифференциального уравнения вида

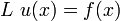Функция Грина — это обратный оператор к 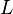. Поэтому ее нередко символически обозначают как .

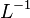Если ядро L не тривиально, то функция Грина не единственна. Однако на практике использование принципа симметрии, граничных условий и/или других дополнительных условий позволяет определить конкретную функцию Грина. Следует помнить, что, вообще говоря, функция Грина — не обычная, а обобщённая функция, то есть она может выпадать из класса обычных функций, например, иметь особенности вида дельта-функции или её производных.

Функция Грина — это также полезный инструмент для решения волнового уравнения, уравнения диффузии и квантово механических уравнений, где функция Грина оператора Гамильтона играет важнейшую роль и связана с плотностью состояний. В физике функция Грина обычно определяется с противоположным знаком:

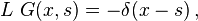
что не меняет существенно её свойства.

Если оператор трансляционно инвариантен, то есть если L имеет постоянные коэффициенты по отношению к x, то функция Грина может быть выбрана в виде конволюционного оператора

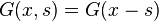
В таком случае она совпадает с импульсной переходной функцией из теории линейных стационарных систем.

Иногда, когда неоднородное уравнение содержит в правой части постоянный коэффициент, то есть имеет вид 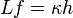, функция Грина 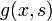также определяется с учётом этого коэффициента, то есть, по определению тогда она есть решение уравнения^[1]

.

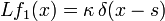В этом случае решение исходного неоднородного уравнения 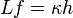с произвольной функцией 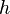в правой части записывается как

.
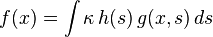