Для параболических уравнений

Уравнение теплопроводности, уравнение Шредингера и уравнения диффузии можно представить в виде уравнения в частных производных:

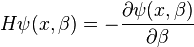(2)

где 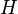— эрмитов оператор, 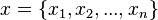- пространственные координаты

· для уравнения теплопроводности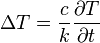

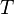— температура, .

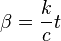· для уравнения Шредингера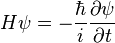

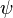— волновая функция, .

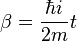· для уравнения диффузии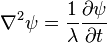

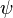— концентрация вещества, .

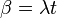Собственные функции 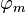оператора 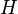образуют полную ортонормированную систему и удовлетворяют уравнению

.

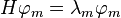Предположим, что решение уравнения (1) можно представить в виде:

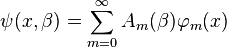Подставляя в уравнение (2) предполагаемую форму решения, получаем:

.

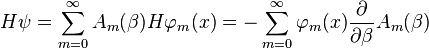Таким образом:

.

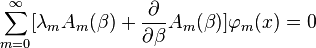Это уравнение должно выполняться для всех m. Получаем уравнение:

,

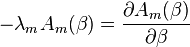откуда

.

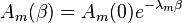Следовательно, решение исходного уравнения (2) можно представить в виде:

.

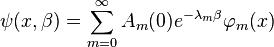Считая ряд (3) равномерно сходящимся, можно найти, что:

,

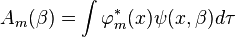где 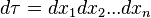— элемент объёма.

Из этой формулы следует:

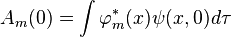
Итак, если задано начальное состояние, то

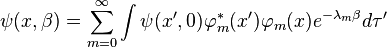
Это уравнение можно представить в более удобной форме:

,

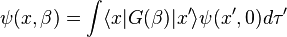где:

.

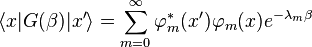Это выражение называется функцией Грина для уравнения (1).

Функция Грина для лапласиана может быть легко получена из теоремы Грина.

Для получения теоремы Грина, начнём с закона Гаусса :

.

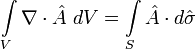Допустим 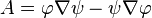и подставим в закон Гаусса . Вычислим 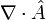и применим цепное правило для оператора:

.

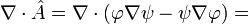
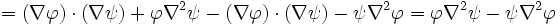Подставляя результат в теорему Гаусса, мы получаем теорему Грина:

.

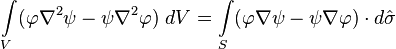Предполагая, что наш линейный дифференциальный оператор 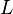Лапласиан, 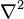, и то, что у нас имеется для него функция Грина 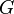. Определение функции Грина в этом случае запишется в виде:

.

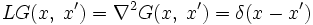Положим 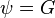в теореме Грина. Тогда получим:

.

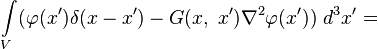
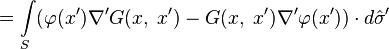Используя выражение, мы можем решить уравнение Лапласа ( 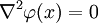) и уравнение Пуассона ( 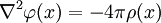) с граничными условиями Неймана или Дирихле. Другими словами, мы можем найти решение 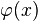всюду внутри заданной области, если (1) значение 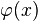задано на границе этой области (граничные условия Дирихле), или (2) нормальная производная 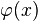задана на границе этой области (граничные условия Неймана).

Пусть нас интересует решение 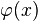внутри области.

В этом случае интеграл 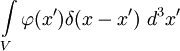упрощается до 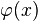в силу основного свойства дельта-функции, и мы имеем:

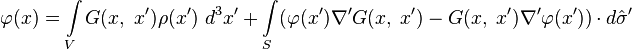
Эта формула выражает известное свойство гармонических функций, состоящее в том, что если известно значение нормальной производной на границе области, то известны и все значения функции в любой внутренней точке этой области.

В электростатике 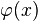понимается как электростатический потенциал, 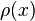как плотность электрического заряда, а нормальная производная 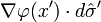как нормальная составляющая электрического поля.

При решении краевой задачи Дирихле функция Грина выбирается в виде 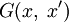. Эта функция обращается в нуль, когда 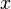или 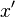находится на границе раздела; и наоборот, решая краевую задачу Неймана, следует выбирать функцию Грина так, чтобы на поверхности обращалась в нуль её нормальная производная. Таким образом в интеграле по поверхности остаётся только одно из двух слагаемых.

При отсутствии граничных условий функция Грина для лапласиана имеет вид:

.

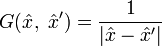Считая граничную поверхность бесконечно большой и подставляя в это выражение функцию Грина, мы придём к аналогичному выражению для электрического потенциала через электрическую плотность заряда.

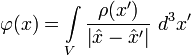
Раздел 4. Специальные функции математической физики.

4.1. Интегралы Эйлера (1-го и 2-го рода).