Метод разделения переменных для струны, закрепленной на концах

Физический смысл дивергенции векторного поля.

Инвариантное определение дивергенции. В разделе 17.2.2.1. Дивергенция векторного поля мы определили дивергенцию как выражение в определённой системе координат : 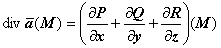. Теорема Остроградского позволяет понять смысл дивергенции поля в точке М как объективного атрибута векторного поля без использования координатной системы. Пусть 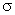- замкнутая поверхность, окружающая точку М, V - тело, заключенное внутри 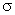, 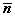- вектор единичной внешней нормали к 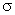. Тогда 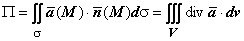. По теореме о среднем для тройного интеграла существует точка 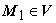такая, что 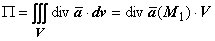. Следовательно, 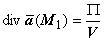. Отношение значения некоторой физической величины к объёму принято называть средней плотностью этой величины в объёме; если объём стягивается к точке М, предел средней плотности называется локальным значением плотности в точке М. Таким образом, мы можем трактовать 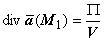как среднюю плотность потока в объёме V. Будем теперь стягивать 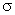к точке М, при этом и V стягивается к точке М; 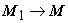, и, вследствие непрерывности 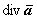, 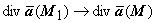. Поэтому 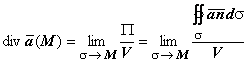будет равна плотности потока в точке М, и так как плотность потока определяется независимо от выбора какой-либо системы координат, то дивергенция векторного поля инвариантна относительно выбора координатной системы.

Используем теперь гидродинамическую интерпретацию поля для выяснения физического смысла дивергенции. Пусть 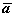(M) - стационарное поле скоростей несжимаемой жидкости. В каком случае поток 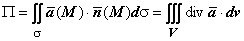через замкнутую поверхность 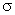может быть отличен от нуля, т.е. в каком случае из V вытекает больше жидкости, чем втекает (при П>0) или наоборот (при П<0)? Ясно, что П>0 может быть только в том случае, если в V появляется дополнительная жидкость, т.е. в V имеются источники поля. П<0 может быть только в том случае, если в V исчезает часть жидкости, т.е. в V имеются стоки поля. Поэтому как плотность потока в точке М определяет силу источника (при >0) или стока (при <0) в точке М.

По аналогии с полем скоростей жидкости считают, что дивергенция определяет силу источников и стоков поля в любом поле 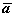(M).

Оператор Лапласа.

Задача Коши для одномерного волнового уравнения на прямой

ФОРМУЛА ДАЛАМБЕРА

Изучение методов построения решений краевых задач для уравнений гиперболического типа мы начинаем с задачи с начальными условиями для неограниченной струны (задача Коши).

(1) u_tt - a² u_xx = 0, .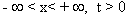

(2) 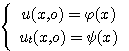, t > 0.

Преобразуем это уравнение к каноническому виду, содержащему смешанную производную.

Уравнение характеристик: dx² - a² dt² = 0 распадается на два уравнения: dx - adt = 0 , dx + adt = 0

интегралами которых являются прямые x - at = c₁, x + at = c₂.

Вводим, как обычно новые переменные: ξ = x + at, η = x - at. Уравнение колебаний струны преобразуем к виду:

(3) u_{ξ η} = 0

Проинтегрируем (3) по переменной ξ :

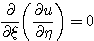
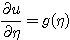
Проинтегрируем полученное равенство по η и получим:

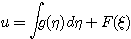
Итак общее решение дифференциального уравнения (3) может быть записано:

u(ξ, η) = F(ξ) + G(η)

Возвращаясь к исходным переменным (x,t), получаем:

(4) u(x,t) = F(x + at) + G(x - at)

Определим функции F и G таким образом, чтобы удовлетворялись начальные условия. Для этого подставим общее решение в начальные условия (2):

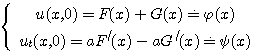
Интегрируя второе равенство, получим:

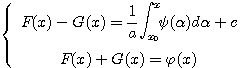
Из полученных равенств находим:

(5)

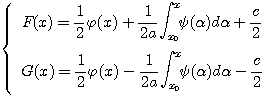
Таким образом, мы определили функции F и G через заданные функции φ и ψ . Подставляя в (4) найденные значения получим:

u(x,t) = F(x + at) + G(x - at)

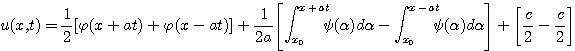
(6)

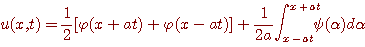
Формула (6) называется формулой Даламбера.

Она определяет решение задачи Коши для волнового уравнения.

Метод разделения переменных для струны, закрепленной на концах