Часть 2. элементы теории обыкновенных дифференциальных уравнений

Часть 2. ЭЛЕМЕНТЫ ТЕОРИИ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Дифференциальные уравнения занимают особое место в ма­тематике и имеют многочисленные приложения в большом спектре наук. Исследования природных процессов и изучение закономерностей общественных процессов приводят к построе­нию математических моделей, основой которых являются диф­ференциальные уравнения.

В дифференциальных уравнениях неизвестная функция со­держится вместе со своими производными. Основной задачей теории дифференциальных уравнений является изучение функ­ций, представляющих собой решения этих уравнений.

В этой части излагаются элементы теории обыкновенных дифференциальных уравнений, когда неизвестные функции за­висят от одной переменной. Теория дифференциальных урав­нений, когда неизвестные функции зависят от нескольких пере­менных — уравнения в частных производных, является более сложной и представляет специальный раздел математики.

Глава 9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Основные понятия

Базовые определения

Определение 1. Уравнение вида

где х — независимая переменная, у и у' — соответственно не­известная функция и ее производная, называется дифференци­альным уравнением первого порядка.

Примеры дифференциальных уравнений первого порядка:

В случае когда из уравнения можно выразить у', оно имеет вид

Уравнение (9.1) называется уравнением первого порядка, раз­решенным относительно производной. В дальнейшем будем рассматривать уравнения первого порядка именно такого ви­да. Примеры уравнений, разрешенных относительно производ­ной:

Приведем примеры уравнений, которые можно разрешить относительно производной неизвестной функции у'.

Пример 1. (y')² = x² + у², откуда получаем два уравнения первого порядка у' = ± .

Определение 2. Решением дифференциального уравнения первого порядка называется функция у = φ(x), определенная на некотором интервале (а, b), которая при подстановке в урав­нение обращает его в тождество.

Например, функция у = х² тождественно обращает в нуль левую часть уравнения ху' — 2х² = 0 и потому представляет собой решение этого уравнения.

В теории дифференциальных уравнений основной задачей является вопрос о существовании и единственности решения. Ответ на него дает теорема Коши, которую мы приводим без доказательства.

ТЕОРЕМА 1. Пусть дано дифференциальное уравнение (9.1). Если функция f(x,y) и ее частная производная f'_y(x,y) непре­рывны в некоторой области D плоскости Оху, то в неко­торой окрестности любой внутренней точки (x₀, у₀) этой области существует единственное решение уравнения (9.1), удовлетворяющее условию у = у₀ при х = x₀.

График решения дифференциального уравнения называет­ся интегральной кривой. В области D содержится бесконечно много интегральных кривых. Теорема Коши гарантирует, что при соблюдении определенных условий через каждую внутрен­нюю точку области D проходит только одна интегральная кри­вая. Условия, которые задают значение функции у₀ в фиксиро­ванной точке x₀, называют начальными условиями (условиями Коши) и записывают в такой форме:

Задача нахождения решения уравнения (9.1), удовлетворя­ющего условию (9.2), называется задачей Коши — из множес­тва интегральных кривых выделяется та, которая проходит через заданную точку (x₀, y₀) области D.

В ряде случаев, когда условия теоремы Коши не выполне­ны, через некоторые точки плоскости Оху либо не проходит ни одной интегральной кривой, либо проходит более одной ин­тегральной кривой; эти точки называются особыми точками данного дифференциального уравнения.

Определение 3. Общим решением уравнения (9.1) называет­ся функция у = φ(x, С), удовлетворяющая этому уравнению при произвольном значении постоянной С.

Определение 4. Частным решением уравнения (9.1) в облас­ти D называется функция у = φ(х,С₀), полученная при опре­деленном значении постоянной С = С₀.

Общее решение у = φ(x, С) описывает семейство интег­ральных кривых на плоскости Оху. Условия Коши (9.2) фик­сируют произвольную постоянную С и позволяют выбрать из семейства интегральных кривых уравнения (9.1) одну интег­ральную кривую у = φ(x,C₀), проходящую через заданную точку (x₀, y₀).

Например, рассмотрим уравнение у' = 2х. Правая часть этого уравнения удовлетворяет условиям теоремы Коши во всех точках плоскости Оху (функции f(x, у) = 2х и f'_y(x, у) 0 определены и непрерывны на всей плоскости Оху). Нетруд­но видеть, что общим решением уравнения является функция у = х² + С, где С — произвольная постоянная, описывающая семейство парабол (рис. 9.1). Для отыскания частного решения зададим произвольные начальные условия (9.2) и подставим их в формулу общего решения; получаем, что С = у₀ — x₀², откуда находим частное решение у = х² + у₀ – х₀². Это частное решение выделяет из семейства парабол одну, проходящую через точку (х₀, у₀).

Неполные уравнения

Определение 6. Дифференциальное уравнение первого поряд­ка (9.1) называется неполным, если функция f явно зависит только от одной переменной: либо от х, либо от у.

Различают два случая такой зависимости.

1. Пусть функция f зависит только от х. Переписав это уравнение в виде

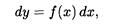
нетрудно убедиться, что его решением является функция

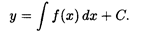
2. Пусть функция f зависит только от у, т.е. уравнение (9.1) имеет вид

Дифференциальное уравнение такого вида называется авто­номным. Такие уравнения часто употребимы в практике мате­матического моделирования и исследования природных и физи­ческих процессов, когда, например, независимая переменная х играет роль времени, не входящего в соотношения, описываю­щие законы природы. В этом случае особый интерес представ­ляют так называемые точки равновесия, или стационарные точки,— нули функции f(у), где производная у' = 0.

Решение уравнения (9.6) методом разделения переменных приводит к функциональному уравнению для определения не­известной функции у = φ(x) (или х = ψ(у)):

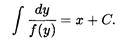
В общей теории дифференциальных уравнений развита те­ория качественного анализа, основанная на исследовании ха­рактера стационарных точек.

Основные понятия теории

Определение 1. Дифференциальным уравнением второго по­рядка называется уравнение вида

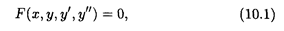
где х — независимая переменная, у — искомая функция, у' и у" — соответственно ее первая и вторая производные.

Примеры дифференциальных уравнений второго порядка:

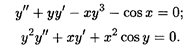
Будем рассматривать уравнения, которые можно записать в виде, разрешенном относительно второй производной:

Как и в случае уравнения первого порядка, решением урав­нения (10.1) называется функция у = φ(x), определенная на некотором интервале (а, b), которая обращает это уравнение в тождество. График решения называется интегральной кривой. Имеет место теорема существования и единственности реше­ния уравнения второго порядка.

ТЕОРЕМА 1 (теорема Коши). Пусть функция f(x, у, у') и ее частные производные 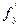и 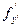, непрерывны в некоторой обла­сти D пространства переменных (x, у, у'). Тогда для любой внутренней точки М₀(х₀, у₀, у'₀) этой области существует единственное решение уравнения (10.2), удовлетворяющее ус­ловиям:

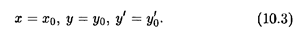
Геометрический смысл этой теоремы (ее доказательство мы не приводим) заключается в том, что через заданную точку (x₀, y₀) на координатной плоскости Оху проходит единствен­ная интегральная кривая с заданным угловым коэффициентом y₀' касательной (рис. 10.1).

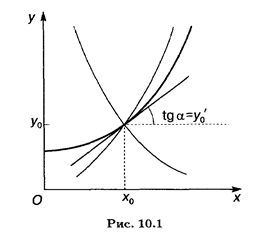
Условия (10.3) называются начальными условиями, а зада­чу отыскания решения уравнения (10.2) по заданным началь­ным условиям называют задачей Коши.

Общим решением уравнения (10.2) в некоторой области D называется функция у = φ(х, С₁, С₂), если она является реше­нием этого уравнения при любых постоянных величинах С₁и C₂, которые могут быть определены единственным образом при заданных начальных условиях (10.3). Частным решением уравнения (10.2) называется общее решение этого уравнения при фиксированных значениях постоянных С₁ и C₂: у = φ(х, С₁⁰, С₂⁰).

Рассмотрим для пояснения уравнение у" = 0. Его общее решение получается при двухкратном интегрировании этого уравнения:

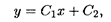
где С₁ и C₂ — произвольные постоянные. Это решение пред ставляет собой семейство прямых, проходящих в произвольных направлениях, причем через каждую точку плоскости Охy проходит бесконечное число таких прямых. Поэтому для выделения частного решения, проходящего через заданную точку (х₀, y₀), следует задать еще и угловой коэффициент прямой, совпадающей в данном случае со своей касательной. Например, найдем частное решение, удовлетворяющее начальным условиям

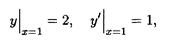
т.е. нужно найти прямую, проходящую через точку M (l, 2), с угловым коэффициентом, равным единице. Подстановка на­чальных условий в общее решение уравнения приводит к сис­теме двух линейных уравнений относительно постоянных С₁и C₂

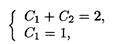
откуда С₁ = 1, C₂ = 1. Таким образом, искомое частное реше­ние — это прямая у = х + 1.

Часть 2. ЭЛЕМЕНТЫ ТЕОРИИ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Дифференциальные уравнения занимают особое место в ма­тематике и имеют многочисленные приложения в большом спектре наук. Исследования природных процессов и изучение закономерностей общественных процессов приводят к построе­нию математических моделей, основой которых являются диф­ференциальные уравнения.

В дифференциальных уравнениях неизвестная функция со­держится вместе со своими производными. Основной задачей теории дифференциальных уравнений является изучение функ­ций, представляющих собой решения этих уравнений.

В этой части излагаются элементы теории обыкновенных дифференциальных уравнений, когда неизвестные функции за­висят от одной переменной. Теория дифференциальных урав­нений, когда неизвестные функции зависят от нескольких пере­менных — уравнения в частных производных, является более сложной и представляет специальный раздел математики.