БИЛЕТ.Интерполяционный многочлен Лагранжа.
Пусть функция задана таблицей (1). Построим интерполяционный многочлен Ln(x), чья степень не превосходит n, и для которого выполнены условия (2).
Ln(x) ищем в виде Ln(x)= l0(x)+ l1(x)+ l2(x)+…+ ln(x),
| Где li(x) – многочлен степени n, причем li (xk | ìy | , | если | i = k | |||||
| ) = í | i | i ¹ k | |||||||
| î0, | если | ||||||||
| Многочлен li(x) составлен следующим образом: | |||||||||
| li(x)=ci (x-x0) (x-x1)… (x-xi-1) (x-xi+1)… (x-xn), | где | ci=const. | |||||||
| ci = | yi | ||||||||
| (xi | - x0)...(xi - xi-1)(xi - xi+1)...(xi - xn ) | ||||||||
Таким образом, получим интерполяционный многочлен Лагранжа:
| n | (x - x0 )...(x - xi-1 )(x - xi+1 )...(x - xn ) | ||
| Ln (x)=å yi | . | ||
| (xi - x0 )...(xi - xi-1 )(xi - xi+1 )...(xi - xn ) | |||
| i=0 |
Погрешность вычисляется по формуле:
| Rn (x) | £ | M n+1 | × | Õn+1 (x) | , x Ï[x0 , xn ] , где | M n+1=max | f | |||||||
| (n +1)! | ||||||||||||||
| Õn+1 (x) = (x - x0 )(x - x1 )...(x - xn ) . |
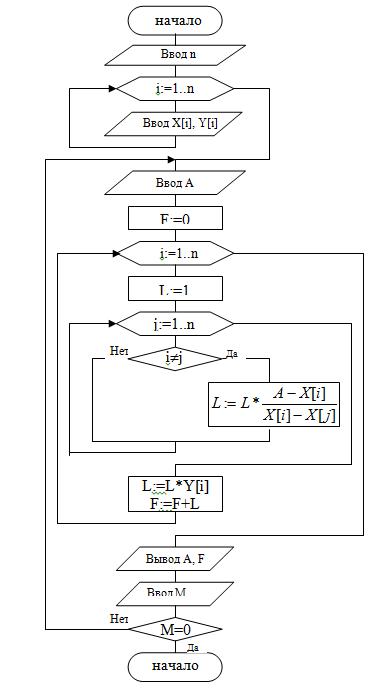
const k=30;
type vektor=array[1..k] of real; var x,y: vektor;
n,i,j: byte;
l,f,a,m: real;
begin
write('Введите количество узлов интерполирования writeln('Введите парами значения Х и Y');
for i:=1 to n do readln(X[i],y[i]); repeat
write('Введите заданное значение аргумента - '); readln(A);
(n+1) (x)

- '); readln(n);
F:=0;
for i:=1 to n do
begin L:=1;
for j:=1 to n do
if i<>j then L:=L*(A-X[j])/(X[i]-X[j]);
L:=L*Y[i];
F:=F+L; end;
writeln('При Х=',A:5:3,' F(',A:5:3,') = ',F:10:6);
writeln; writeln('Если хотите продолжить, введите 1,'); writeln('в противном случае введите 0'); readln(m)
until M=0 end.
14БИЛЕТ.многочлен Ньютона для равноотстоящих узловРассмотрим случай, когда h=xi+1 – xi=const (i=0, 1, …). Рассмотрим конечные разности:
Dyi = yi+1- yi –конечные разности1-го порядка–разности между значениями функции в
соседних узлах.
| D2 yi = Dyi+1- Dyi | = ( yi+2 - yi+1 ) - ( yi+1 - yi ) = yi+2 - 2 yi+1 + yi – конечные разности 2-го порядка – | ||||||||
| разности между конечными разностями 1-го порядка. | |||||||||
| D3 yi = D1 yi+1- D2 yi =( yi+3-2yi+2+ yi+1)-( yi+2-2yi+1+ yi )= yi+3-3yi+2+3yi+1- yi | –конечные | ||||||||
| разности 3-го порядка. | |||||||||
| … | k(k -1) | ||||||||
| Dk = yi+k | - kyi+k -1 | + | yi+k -2-...+(-1)k yi | – конечные разности k-го порядка. | |||||
| 2! | |||||||||
| Конечные разности удобно вычислять в таблице: | |||||||||
| xi | yi | D yi | D2 yi | D3 yi | |||||
| x0 | y0 | D y0 | D2 y0 | D3 y0 | |||||
| x1 | y1 | D y1 | D2 y1 | D3 y1 | |||||
| x2 | y2 | D y2 | D2 y2 | ||||||
| x3 | y3 | D y3 | |||||||
| x4 | y4 |
Первая интерполяционная формула Ньютона
Будем искать интерполяционный многочлен Ньютона в виде многочлена n-ой степени:
Pn(x) = a0+ a1(x-x0) + a2(x-x0)(x-x1) +…+ an(x-x0)…(x-xn-1) (3)
Коэффициенты a0, a1, …, an находятся из условия совпадения значения исходной функции f(x) и многочлена Pn(x) в узлах интерполяции: ak = Dky0 .
k!h k
Пусть x - x0 = t , тогда x = x0 + ht , соответственно h

x - x x - x - h
= = t -1
hh
x - x2 = x - x0 - 3h = t - 2
hh10




…
Подставив в формулу (3), получим:
| P (x)= P (x | + th)= y | + tDy | + | t(t -1) | D2 y | + ... + | t(t -1)...(t - n +1) | Dn y | – | первая | ||||||||||||||||||||||||||||
| n | n | 2! | n! | |||||||||||||||||||||||||||||||||||
| интерполяционная формула Ньютона. | ||||||||||||||||||||||||||||||||||||||
| Погрешность вычислений оценивается следующим образом: | ||||||||||||||||||||||||||||||||||||||
| R | (x) | » | t(t -1)(t -2)...(t - n) | Dn+1 y | ||||||||||||||||||||||||||||||||||
| n | (n +1)! | t(t -1) | ||||||||||||||||||||||||||||||||||||
| Так при n=2 | ||||||||||||||||||||||||||||||||||||||
| P (x)» y | + tDy | + | D2 y | |||||||||||||||||||||||||||||||||||
| n | 2! | |||||||||||||||||||||||||||||||||||||
| t(t -1)(t -2) | ||||||||||||||||||||||||||||||||||||||
| R | (x) | » | D3 y ,гдеD3 y =max | D3 y | m | |||||||||||||||||||||||||||||||||
| n | 3! | 0£m£3 | ||||||||||||||||||||||||||||||||||||
