Интерполяционный многочлен Лагранжа

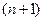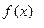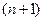Пусть имеется значение ф-ции в различных точках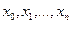

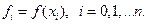
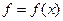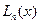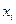Надо найти функцию, которая смогла бы дать значение в произвольной точке . Для этого часто используют алгебраический многочлен степени , который в точках принимает заданные значения, т.е. 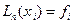(6.15)

Такой многочлен называетсяинтерполяционным. Точки 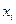называются узлами интерполяции.

Теорема существования. Существует единственный интерполяционный многочлен 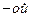степени, удовлетворяющий условиям (6.15).

Доказательство. Существование подобного многочлена устанавливается

непосредственно путем его выписывания. Пусть 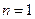. Тогда

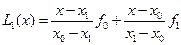. (6.16)

При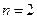

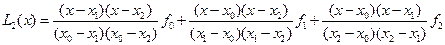. (6.17)

В общем случае, при любом натуральном

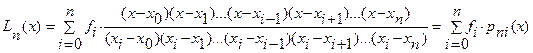. (6.18)

Непосредственной подстановкой в (6.16 - 6.18) убеждаемся, что .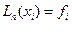

Нетрудно увидеть, что многочлен 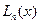в (6.18) имеет степень . Видно, что

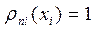, a .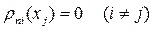

Единственность интерполяционного многочлена (6.18) доказывается методом от противного. Пусть кроме 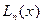имеется ещё некоторый алгебраический многочлен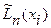 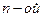степени, удовлетворяющий условиям

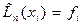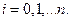, (6.19)

Тогда, согласно (6.15) и (6.19)

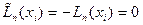
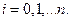(6.20)

Если в точках 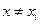разность (6.20) не равна нулю, то мы получим многочлен

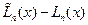степени не выше и в силу основной теоремы высшей алгебры он имеет не более корней. Но из (6.20) следует, что мы уже имеем 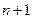корень. Чтобы избежать противоречия, мы должны согласиться, что .

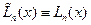Это и есть доказательство единственности интерполяционного многочлена.

Интерполяционный многочлен (6.18) называется интерполяционным многочленом Лагранжа, а функции 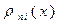-лагранжевыми коэффициентами.

Для вычисления 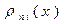удобно применять следующее расположение разностей, подчеркнув разности, расположенные на главной диагонали:

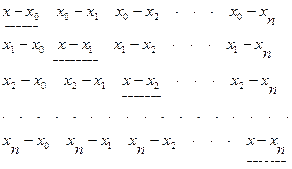
Обозначим произведение элементов 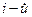строки через D_i , а произведение элементов главной диагонали через 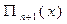, т.е 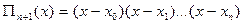. Тогда

.

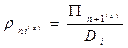
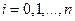Иногда бывает полезным для упрощения вычислений использовать инвариантность коэффициентов Лагранжа относительно линейной подстановки: если

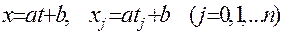, то .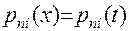

В случае равностоящих узлов имеются таблицы для лагранжевых коэффициентов и процесс вычисления значительно облегчается.

Схема Эйткена.

Если требуется найти не общее выражение L_n(x), а лишь его значения при конкретных х, и при этом значения функции даны в достаточно большом количестве узлов, то удобно пользоваться интерполяционной схемой Эйткена.

Согласно этой схеме последовательно вычисляются многочлены

,

,

----------------------------------------------------------------------------------------

­­­­­­­­­­­­­­­­­­­­­­­­­­­

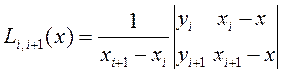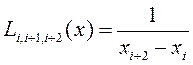
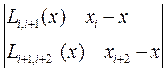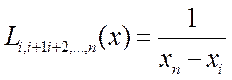
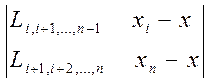и т.д.

Интерполяционный многочлен 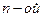степени (принимающий в точках 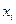значения 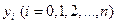) записывается следующим образом:

.

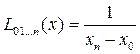
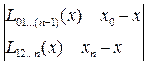Вычисления по схеме Эйткена удобно располагать в такой таблице

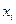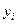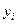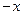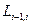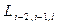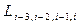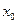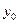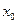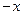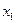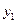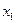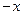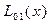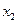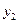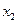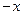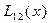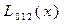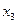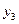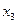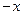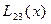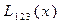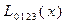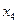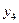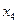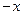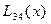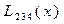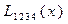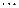Вычисления по схеме Эйткена обычно ведут до тех пор, пока последовательные значения 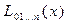и 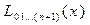не совпадут в пределах заданной точности. Схема Эйткена легко реализуется на ЭВМ и обеспечивает возможность автоматического контроля точности вычислений.

Замечания.

1. Непосредственной проверкой можно убедиться, что .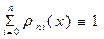

Это тождество может служить контролем при вычислении лагранжевых коэффициентов .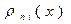

2. Интерполяционный многочлен (6.18) линейно зависит от значений функции .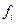

Поэтому интерполяционный многочлен для суммы двух функций равен сумме интерполяционных многочленов для слагаемых.

Пример. Построить интерполяционный многочлен Лагранжа по табличным данным:

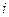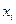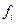Решение. Согласно (6.18) при 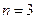имеем

.

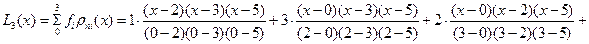
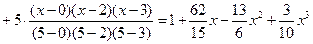Погрешность интерполяции.

Можно написать следующее равенство.

,

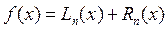где 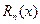- остаточный член или погрешность интерполяции.

Для оценки остаточного члена предположим, что

,

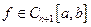где - отрезок, содержащий все узлы интерполяции .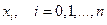

Будем искать 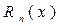в виде:

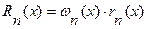, (6.22)

где 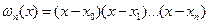, (6.23)

r_n(x) - некоторая функция от .

Воспользуемся следующим приемом:

Введем в рассмотрение фун-цию .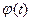

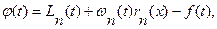(6.24)

оставив в составе 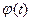функцию r_n(x) при некотором произвольном фиксированном 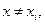но .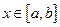

Ф-ция 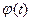обращается в нуль пр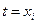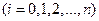и , , и 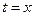(на основании формул (6.15),(6.21), (6.22), (6.23) ).

Т.е. она принимает нулевые значения не менее чем в 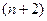точках отрезка , на котором изменяется 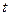. По теореме Ролля первая производная по t 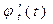обращается в нуль, по крайней мере в 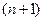точке интервала 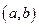, 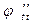равна нулю минимум в точках этого интервала и т.д. Продолжая эти рассуждения и дойдя до 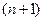производной можно сказать, что найдется хотя бы одна точка 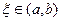, в которой .

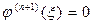Перепишем теперь последнее уравнение, предварительно продифференцировав 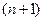по 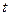его левую и правую части:

.

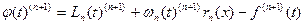Так как 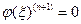, а 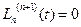в любой точке 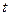, как производная многочлена 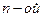степени, то для точки 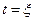можно написать равенство

,

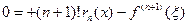где 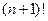- производная 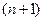- го порядка от .

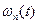Следовательно,

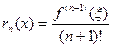(6.25)

или 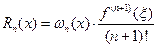, (6.26)

и 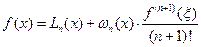, (6.27)

где 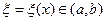- некоторая точка интервала 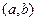, положение которой зависит от рассматриваемого значения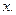

Из последнего равенства (6.27) можно оценить погрешность интерполяции в текущей точке :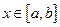

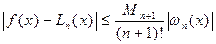. (6.28)

Здесь .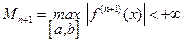

Оценка максимальной погрешности интерполяции на всем отрезке :

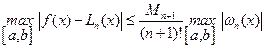. (6.29)

Пример. Оценить погрешность приближения функции 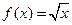в точке 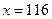и на всем отрезке , где 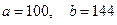, с помощью интерполяционного многочлена Лагранжа второй степени 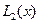, построенного с узлами .

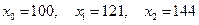Решение. Здесь 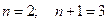. Следовательно, нам потребуются производные до 3- ^го порядка включительно.

.

.

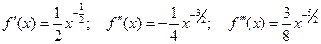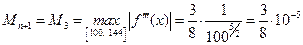На основании (6.28)

.

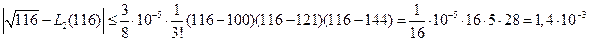А в силу оценки (6.29):

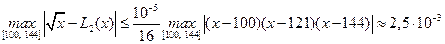
Здесь опущено нахождение максимума .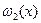

6.4. Линейная интерполяция.

Перепишем многочлен Лагранжа для случая .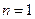

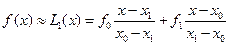(6.30)

Интерполяция в виде такого многочлена называется линейной.

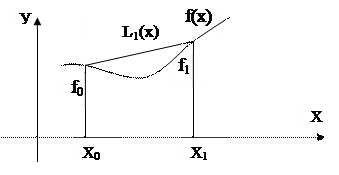Рис.6.3. К вопросу о линейной интерполяции.

Введем обозначения 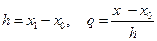. Тогда .

.

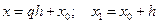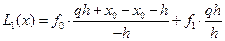Итак: 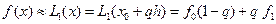. (6.31).

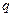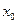Величина называется фазой интерполяции, которая изменяется в пределах от 0 до 1, когда пробегает значения от до .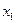

Геометрически линейная интерполяция означает (рис. 6.3) замену графика функции на отрезке 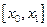хордой, соединяющей точки .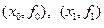