Интерполяционный многочлен Лагранжа 5 страница
Дана функция 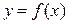 своими значениями
своими значениями 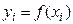 , где
, где 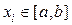 ,
, 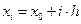 ,
, 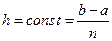 ,
, 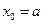 ,
, 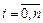 . Найти интерполирующую функцию определенного класса
. Найти интерполирующую функцию определенного класса 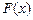 , такую что
, такую что 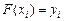 , для
, для 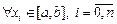 .
.
Задача интерполяции заключается в нахождении значения функции 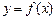 при
при 
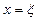 , для чего полагают, что
, для чего полагают, что 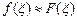 .
.
Рассмотрим решение задачи интерполяции для функции заданной таблично, используя метод Ньютона для равноотстоящих узлов.
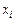 | 2,00000000 | 2,14000000 | 2,28000000 | 2,42000000 | 2,56000000 | 2,70000000 | 2,84000000 |
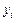 | 7,274400 | 7,715100 | 7,889900 | 7,737300 | 7,200500 | 6,231200 | 4,791600 |
Найти 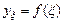 , при
, при 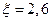 .
.
Так как 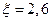 находится в конце таблицы, то применяем для решения задачи приближения вторую интерполяционную формулу Ньютона
находится в конце таблицы, то применяем для решения задачи приближения вторую интерполяционную формулу Ньютона
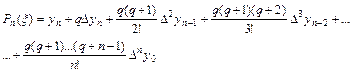
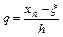 .
.
Тогда 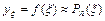 ,
, 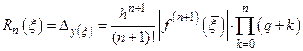 ,
, 
Составим конечные разности
 | 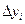 | 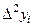 | 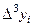 | 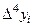 | 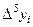 | 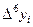 |
| 7,7373000 | -0,2355480 | -0,0657040 | -0,0610118 | 0,0743632 | -0,0920959 | 0,1105114 |
| 7,5017520 | -0,3012520 | -0,1267158 | 0,0133514 | -0,0177327 | 0,0184155 | |
| 7,2005000 | -0,4279678 | -0,1133644 | -0,0043813 | 0,0006828 | ||
| 6,7725322 | -0,5413322 | -0,1177457 | -0,0036985 | |||
| 6,2312000 | -0,6590779 | -0,1214442 | ||||
| 5,5721221 | -0,7805221 | |||||
| 4,7916000 |
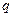 | 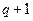 | 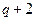 | 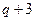 | 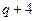 | 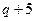 |
| -1,7143 | -0,7143 | 0,2857 | 1,2857 | 2,2857 | 3,2857 |
Составим таблицу для вычисления слагаемых во второй интерполяционной формуле Ньютона:
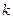 | 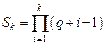 | 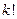 | 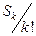 | 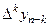 | 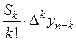 |
| 3,3782 | 720,0000 | 0,004691923 | -0,0018000 | -8,44546E-06 | |
| 1,028143036 | 120,0000 | 0,008567859 | 0,0020000 | 1,71357E-05 | |
| 0,449812578 | 24,0000 | 0,018742191 | 0,0105000 | 0,000196793 | |
| 0,349854227 | 6,0000 | 0,058309038 | -0,0378000 | -0,002204082 | |
| 1,224489796 | 2,0000 | 0,612244898 | -0,4703000 | -0,287938776 | |
| -1,7143 | 1,0000 | -1,714285714 | -1,4396000 | 2,467885714 | |
| 4,7916000 | 4,7916 | ||||
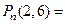 | 6,96954834 |
Графическая интерпретация исходных значений и результата дают следующую картину, где точкой показан полученный результат: 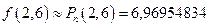 . Из данного рисунка можно сказать, что найденное приближенное решение задачи интерполяции вполне отвечает исходным данным.
. Из данного рисунка можно сказать, что найденное приближенное решение задачи интерполяции вполне отвечает исходным данным.
Оценка погрешности приближения 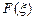 .
.
Оценим погрешность приближения с помощью выражения 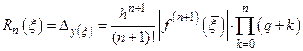 ,
, 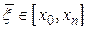 . Для этого оценим
. Для этого оценим 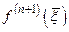 с помощью выражения
с помощью выражения 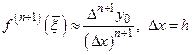 . Тогда получим следующую погрешность
. Тогда получим следующую погрешность 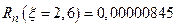 .
.
Получим решение: 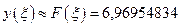 ,
, 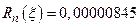 .
.
Определим число верных знаков. Так как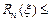 0,00005, то при
0,00005, то при 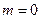 имеем
имеем 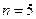 .
.
После округления получим 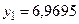 ,
, 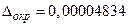 ,
, 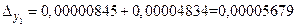 .Так как
.Так как 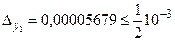 ,то
,то 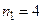 .
.
Округлим 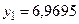 до верных знаков. Получим (используя правило четной цифры)
до верных знаков. Получим (используя правило четной цифры) 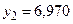 , где
, где 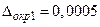 ,
, 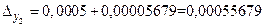 . Так как
. Так как 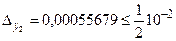 ,то
,то 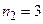 .
.
Округлим 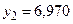 до верных знаков. Получим
до верных знаков. Получим 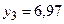 , где
, где 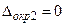 ,
, 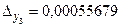 . Так как
. Так как 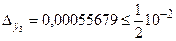 ,то
,то 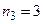 . При этом
. При этом 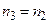 .
.
Следовательно, в полученном результате все знаки верные.
Ответ: 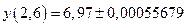 .
.
Порядоквыполнения работы
1. Найти приближенное значение функции при заданном значении аргумента 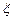 с помощью соответствующего интерполяционного полинома Ньютона, если функция задана в равноотстоящих узлах;
с помощью соответствующего интерполяционного полинома Ньютона, если функция задана в равноотстоящих узлах;  ,
, 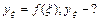 Оценить погрешность полученного значения.
Оценить погрешность полученного значения.
| х0 | 0,9950 | 0,9988 | 0,9512 | 0,3679 | 0,3679 | 0,4311 | 0,6664 | 1,7151 | 1,0806 | 6,8621 | |
| х1 | 1,15 | 1,1424 | 1,1481 | 1,0857 | 0,3064 | 0,2317 | 0,3044 | 0,4329 | 1,7834 | 1,0805 | 7,4816 |
| х2 | 1,3 | 1,2890 | 1,2973 | 1,2182 | 0,2399 | 0,1419 | 0,2198 | 0,2406 | 1,8803 | 0,9042 | 8,0055 |
| х3 | 1,45 | 1,4348 | 1,4462 | 1,3486 | 0,1771 | 0,0842 | 0,1635 | 0,0903 | 1,9696 | 0,5067 | 8,4128 |
| х4 | 1,6 | 1,5796 | 1,5949 | 1,4770 | 0,1237 | 0,0483 | 0,1263 | -0,0178 | 1,9978 | -0,1495 | 8,6805 |
| х5 | 1,75 | 1,7233 | 1,7433 | 1,6034 | 0,0819 | 0,0267 | 0,1021 | -0,0861 | 1,9035 | -1,0918 | 8,7858 |
| х6 | 1,9 | 1,8658 | 1,8914 | 1,7278 | 0,0514 | 0,0142 | 0,0872 | -0,1185 | 1,6344 | -2,3342 | 8,7075 |
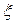 | = | 1,23 | 1,47 | 1,52 | 1,16 | 1,23 | 1,47 | 1,52 | 1,48 | 1,18 | 1,25 |
Контрольные вопросы
1. Как ставится задача интерполирования функции?
2. Как обосновывается существование и единственность интерполяционного многочлена? Как связана его степень с количеством узлов интерполяции?
3. Как строится интерполяционный многочлен Ньютона? В чем особенность этого способа интерполяции?
4. В чем различие в применении первой и второй интерполяционных формул Ньютона?
5. Какова оценка погрешности интерполяционных формул, если интерполируемая функция задана аналитически? Как изменяется эта оценка, когда функция задана таблично?
6. Как используется метод интерполирования для уплотнения таблиц функций?
Практическая работа № 13
Тема: «Приближение табличных функций по методу наименьших квадратов»
Основные вопросы: Постановка задачи. Эмпирическая функция. Полиноминальное приближение по методу наименьших квадратов. Понятие уклонения, среднеквадратичного уклонения. Квадратичное отклонение.
Краткие теоретические сведения: На практике часто возникает необходимость найти функциональную зависимость между величинами x и y. Непосредственно функциональную зависимость можно определить визуально, например, по статистическим данным, но неизвестны параметры функции.
К методу аппроксимации, или приближенного восстановления функции по известным ее значениям в ряде точек относится метод наименьших квадратов. Возникает задача о наилучшем подборе так называемых эмпирических формул, которые позволяют аналитически представить данные измерений, статистической обработки экспериментов и наблюдений и т.д. Обычно задача формулируется следующим образом: имеются данные наблюдений в n точках
М1, М2, …,Мn определенной величины u, и получены соответствующие значения этой величины u1, u2, …, un; нужно подобрать такую функцию u=f(M), чтобыона по возможности наиболее точно отражала общую зависимость измеряемой величины u от параметров точек измерений 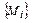 .
.
Задача нахождения эмпирических формул состоит из двух этапов:
- на первом этапе определяется общий вид зависимости f(M) т.е. по ряду наблюдений 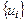 устанавливается вид, который может иметь функция u=f(M), с точностью до постоянных коэффициентов или неизвестных параметров, входящих в нее;
устанавливается вид, который может иметь функция u=f(M), с точностью до постоянных коэффициентов или неизвестных параметров, входящих в нее;
- на втором этапе эти неизвестные параметры подбираются таким образом, чтобы в точках наблюдений 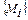 подобранная функция наилучшим способом отвечаладанным измерений
подобранная функция наилучшим способом отвечаладанным измерений 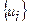 .
.
Пусть в результате первого опыта определено, что измерения в n точках наблюдения М1, М2, …, Мn, давшие соответственно ряд данных u1, u2, …,un, желательно приблизить совокупность функций 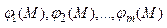 , или эмпирической формулой вида:
, или эмпирической формулой вида:
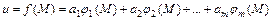 (1)
(1)
где а1, а2, …, аm – неизвестные параметры функции u=f(M).
Второй этап состоит в определении неизвестных параметров. Их нужно выбрать такими, чтобы значения эмпирической функции по возможности давали бы минимальные отклонения в точках от измеренных значений.
Метод наименьших квадратов состоит в минимизации суммы квадратов погрешности функции (1) в точках М1, М2, …, Мnкак функции от m аргументов – неизвестных параметров:
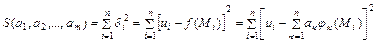 (2)
(2)
Для установления точки минимума функции (2) найдем частные производные этой функции и приравняем их к нулю. Имеем:
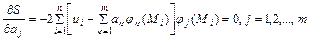 .
.
Переменив порядок суммирования, получаем отсюда систему, состоящую из m линейных алгебраических уравнений относительно m неизвестных параметров 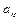 .
.
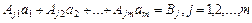 (3)
(3)
Коэффициенты и свободные члены уравнений этой системы определяются по формулам:
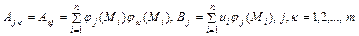 (4)
(4)
Как правило при случайном выборе точек наблюдения система уравнений (3) с коэффициентами (4) имеет единственное решение, дающее набор значений для неизвестных параметров а1, а2, …, аm, соответствующий стационарной точке функции (2). Так как эта функция, состоящая из суммы квадратов несвязок 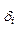 , является положительной, выпуклой вниз и неограниченной в евклидовом пространстве
, является положительной, выпуклой вниз и неограниченной в евклидовом пространстве 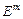 по аргументам а1, а2, …, аm, найденная стационарная точка может быть только точкой ее локального минимума.
по аргументам а1, а2, …, аm, найденная стационарная точка может быть только точкой ее локального минимума.
При обработке данных наблюдений найдем приближение в виде линейной и квадратичной функции. Эмпирическая формула имеет вид  и
и 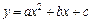 соответственно, сводится к отысканию таких значений параметров
соответственно, сводится к отысканию таких значений параметров 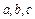 , при которых функции
, при которых функции 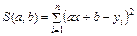 и
и 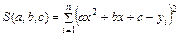 принимает наименьшее значение.
принимает наименьшее значение.
Таким образом, для нахождения линейной и квадратичной функций, наилучшим образом согласованной с экспериментальными данными достаточно решить системы:
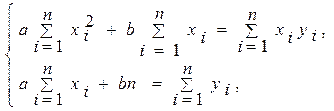
и
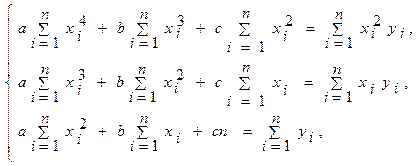
Примеры решения задач
- Имеется шесть измерений пары пееменных (х; у), результаты которых приведены в таблице:
| х | ||||
| у | 0,2 | 0,3 | 1,0 | 1,2 |
Методом наименьших квадратов построить линейную зависимость  . Сравнить полученную зависимость с зависимостью квадратичной.
. Сравнить полученную зависимость с зависимостью квадратичной.
Решение: найдем необходимыедля решения суммы 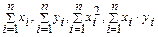 . Промежуточные вычисления представлены в таблице:
. Промежуточные вычисления представлены в таблице:
| i | 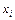 | 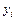 | 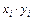 | 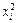 |
| 0,2 | 0,2 | |||
| 0,3 | 0,6 | |||
| 1,0 | 3,0 | |||
| 1,2 | 4,8 | |||
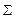 | 2,7 | 8,6 |
Составить систему уравнений:
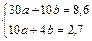
Ее решения 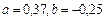 следовательно
следовательно 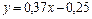 .
.
Составим таблицу для квадратичной зависимости:
| i | 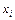 | 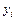 | 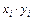 | 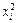 | 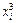 | 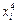 | 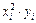 |
| 0,2 | 0,2 | 0,2 | |||||
| 0,3 | 0,6 | 1,2 | |||||
| 1,0 | 3,0 | 9,0 | |||||
| 1,2 | 4,8 | 19,2 | |||||
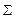 | 2,7 | 8,6 | 29,6 |
Составим систему уравнений:
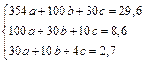
Ее решение 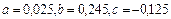 следовательно
следовательно 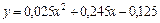 .
.
Сравним величины 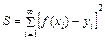 для найденной линейной и квадратичной зависимости. Вычисления представим в таблице:
для найденной линейной и квадратичной зависимости. Вычисления представим в таблице:
| i | 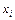 | 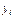 |  | 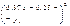 | 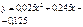 | 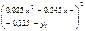 |
| 0,2 | 0,12 | 0,0064 | 0,145 | 0,003025 | ||
| 0,3 | 0,49 | 0,0361 | 0,465 | 0,000625 | ||
| 1,0 | 0,76 | 0,0576 | 0,835 | 0,027225 | ||
| 1,2 | 1,23 | 0,0009 | 1,255 | 0,003025 | ||
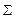 | 0,0994 | 0,0339 |
Как видно квадратура ошибок линейной функции больше квадратуры ошибок квадратичной функции, следовательно, квадратичная функция предпочтительнее.
Порядок выполнения работы
1. Апроксимировать методом наименьших квадратов функции, заданные таблично:
| х | 0,43 | 0,48 | 0,55 | 0,62 | 0,70 | |
| у | 1,63 | 1,73 | 1,87 | 2,03 | 2,22 | |
| х | 0,02 | 0,08 | 0,12 | 0,17 | 0,23 | |
| у | 1,02 | 1,09 | 1,14 | 1,21 | 1,30 | |
| х | 0,15 | 0,20 | 0,25 | 0,30 | 0,35 | |
| у | 6,61 | 6,39 | 6,19 | 6,00 | 5,82 | |
| х | 0,18 | 0,19 | 0,20 | 0,21 | 0,22 | |
| у | 5,61 | 5,46 | 5,32 | 5,19 | 5,06 | |
| х | 1,37 | 1,38 | 1,39 | 1,40 | 1,42 | |
| у | 5,04 | 5,17 | 5,27 | 5,35 | 5,51 | |
| х | 0,18 | 0,19 | 0,20 | 0,22 | 0,24 | |
| у | 5,61 | 5,46 | 5,32 | 5,19 | 5,06 | |
| х | 1,37 | 1,38 | 1,39 | 1,40 | 1,41 | |
| у | 5,04 | 5,17 | 5,32 | 5,47 | 5,62 | |
| х | 1,20 | 7,50 | 13,3 | 19,1 | 25,2 | |
| у | 1,38 | 1,38 | 1,37 | 1,40 | 1,90 | |
| х | 1,20 | 7,50 | 13,3 | 19,1 | 25,2 | |
| у | 1,38 | 1,19 | 1,17 | 1,40 | 1,90 | |
| х | 1,23 | 1,40 | 1,71 | 1,80 | 1,95 | |
| у | 5,04 | 5,17 | 5,43 | 5,53 | 5,62 |
Контрольные вопросы
1. Как ставится задача точечной аппроксимации функции?
2. Как определяется многочлен наилучшего среднеквадратического приближения функции? Как связана его степень с количеством заданных узловых точек? Когда он совпадает с интерполяционным многочленом?
3. Как обосновывается существование и единственность многочлена наилучшего приближения?
4. Какая задача требует составления эмпирической формулы?
5. Как определяются наилучшие параметры выбранной эмпирической формулы? Как называется этот метод?
6. Как оценивается погрешность составленной эмпирической формулы?
Практическое занятие № 13
Тема: «Интерполяция сплайнами»
