Интерполяционный многочлен Лагранжа

Боровец Д.С.

студент 2 курса

заочной формы обучения,

направление «Физико-математическое

образование»

профиль информатика

Курсовая работа

«Интерполяция и наилучшие приближения».

Руководитель:

к.п.н., доцент

Артюхина М.С.

Арзамас, 2014

Содержание.

Введение …………………………………………………………....................………..3

1. Разделенные разности

2. Интерполяционный многочлен Лагранжа

3Интерполирование по схеме Эйткена

4. Интерполяционный многочлен Ньютона

5Приближение и интерполирование функций,

6 Аппроксимация функций методом наименьших квадратов

Заключение………………....................……………………………………………….19

Список литературы…………………………………………...................……………20

Введение.

Если задана функция y(x), то это означает, что любому допустимому значению х сопоставлено значение у. Но нередко оказывается, что нахождение этого значения очень трудоёмко. Например, у(х) может быть определено как решение сложной задачи, в которой х играет роль параметра или у(х) измеряется в дорогостоящем эксперименте. При этом можно вычислить небольшую таблицу значений функции, но прямое нахождение функции при большом числе значений аргумента будет практически невозможно. Функция у(х) может участвовать в каких-либо физико­-технических или чисто математических расчётах, где её приходится многократно вычислять. В этом случае выгодно заменить функцию у(х) приближённой формулой, то есть подобрать некоторую функцию j(х), которая близка в некотором смысле к у(х) и просто вычисляется. Затем при всех значениях аргумента полагают у(х)»j(х).

Большая часть классического численного анализа основывается на приближении многочленами, так как с ними легко работать. Однако для многих целей используются и другие классы функций.

Выбрав узловые точки и класс приближающих функций, мы должны ещё выбрать одну определённую функцию из этого класса посредством некоторого критерия — некоторой меры приближения или «согласия». Прежде чем начать вычисления, мы должны решить также, какую точность мы хотим иметь в ответе и какой критерий мы изберём для измерения этой точности.

Всё изложенное можно сформулировать в виде четырёх вопросов:

· Разделенные разности

· Интерполяционный многочлен Лагранжа

· Интерполяционный многочлен Ньютона

· Аппроксимация функций методом наименьших квадратов

Существуют 3 класса или группы функций, широко применяемых в численном анализе. Первая группа включает в себя линейные комбинации функций 1, х, х², …, хⁿ, что совпадает с классом всех многочленов степени n (или меньше). Второй класс образуют функции cos a_ix, sin a_ix. Этот класс имеет отношение к рядам Фурье и интегралу Фурье. Третья группа образуется функциями e^-az. Эти функции встречаются в реальных ситуациях. К ним, например, приводят задачи накопления и распада.

Что касается критерия согласия, то классическим критерием согласия является «точное совпадение в узловых точках». Этот критерий имеет преимущество простоты теории и выполнения вычислений, но также неудобство из-за игнорирования шума (погрешности, возникающей при измерении или вычислении значений в узловых точках). Другой относительно хороший критерий — это «наименьшие квадраты». Он означает, что сумма квадратов отклонений в узловых точках должна быть наименьшей возможной или, другими словами, минимизирована. Этот критерий использует ошибочную информацию, чтобы получить некоторое сглаживание шума. Третий критерий связывается с именем Чебышева. Основная идея его состоит в том, чтобы уменьшить максимальное отклонение до минимума. Очевидно, возможны и другие критерии.

Более конкретно ответить на поставленные 4 вопроса можно лишь исходя из условий и цели каждой отдельной задачи.

Разделенные разности

Часто экспериментальные данные функциональной зависимости представляются таблицей, в которой шаг по независимой переменной не постоянен. Для работы с таким представлением функции конечные разности и конечно-разностные операторы не пригодны. В этом случае первостепенную роль играют разделенные разности.

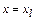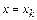Разделенную разность функции f(x) для некоторых двух точек и определяют следующей дробью:

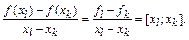
Для построения степенного многочлена, проходящего через заданные точки, необходимо иметь число точек на единицу больше, чем степень многочлена. Согласно определению разделенной разности число их для n точек равно числу сочетаний из n по 2. Это во много раз больше, чем необходимо для построения кривых, проходящих через n точек. Из опыта работы с конечными разностями видно, что разделенных разностей из всего множества достаточно выбрать всего n, но выбрать так, чтобы в их образование входили все (n+1) точек таблицы.

Вполне разумно вычислять разделенные разности только для соседних значений функции в таблице. В этом случае говорят об упорядоченных разделенных разностях. Аргументу табличной функции присваиваются индексы из чисел натурального ряда, начиная с нуля, в результате чего обозначения разделенных разностей для i-той строки таблицы будут .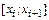

Повторная разность от разделенной разности есть разделенная разность второго порядка:

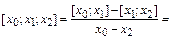
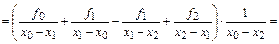
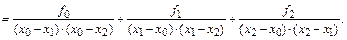
В общем случае разделенная разность n-го порядка имеет вид:

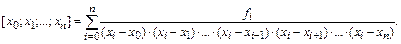
Интерполяционный многочлен Лагранжа

Произведения из скобочных сомножителей в знаменателе каждого слагаемого напоминают своим видом некий степенной многочлен от переменной 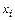, который своими корнями имеет значения 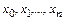, исключая 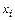. Многочлен от x с корнями в этих же точках, включая и 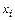, будет иметь вид:

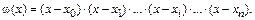
Удаляя тот или иной сомножитель из 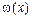, можно по желанию исключить ненужный нуль многочлена. Если взять i-тое слагаемое без 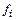из выражения для разделенной разности n-го порядка и умножить его на 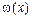, в котором отсутствует сомножитель 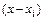, то многочлен степени n будет обладать следующими свойствами:

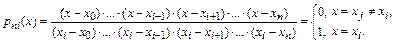
Если умножить 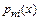на 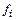, то полученный многочлен степени n будет проходить через точку с координатами 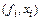и будет равен нулю во всех точках 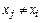. Сумма таких многочленов по всем 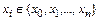определяет интерполяционный многочлен Лагранжа степени n.

.
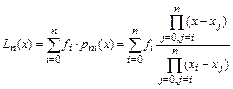