Решение задач по теме: «Действия над комплексными числами»
Цель: Уметь выполнять действия над к.ч., заданными разными формами.
Методические рекомендации
Формы комплексного числа.
1. Алгебраическая 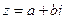
сложение: 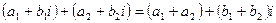
умножение: 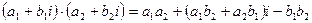
деление: 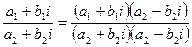
2. Тригонометрическая 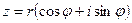
умножение: 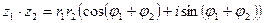
деление: 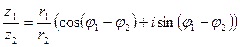
возведение в степень: 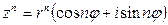
извлечение корня:  ,
, 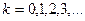
3. Показательная 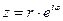
умножение: 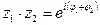
деление: 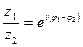
возведение в степень: 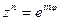
Используя методические рекомендации, выполните задания:
| 1 вариант | 2 вариант |
1. Найдите 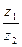 , если , если 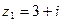 , , 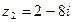 | 1. Найдите 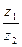 , если , если 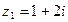 , , 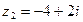 |
2. Найдите модуль к.ч. 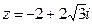 | 2. Найдите модуль к.ч. 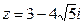 |
3. Найдите 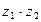 , если , если 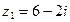 , , 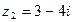 | 3. Найдите 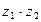 , если , если 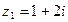 , , 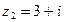 |
4. Изобразите число на комплексной плоскости 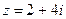 | 4. Изобразите число на комплексной плоскости 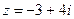 |
5. Вычислите: 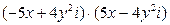 | 5. Вычислите: 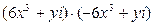 |
6. Разложите на множители: а) 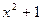 ; б) ; б) 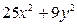 | 6. Разложите на множители: а) 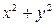 ; б) ; б) 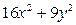 |
7. Решите уравнения: а) 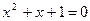 ; б) ; б) 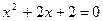 | 7. Решите уравнения: а) 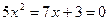 ; б) ; б) 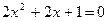 |
8. Выполнить умножение, деление и возведение в степень к.ч. 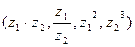 , если а) , если а) 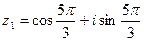 , , 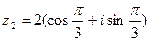 б) б) 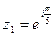 ; ; 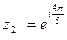 | 8. Выполните умножение, деление и возведение в степень к.ч. 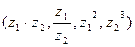 , если а) , если а) 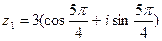 , , 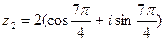 б) б) 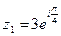 ; ; 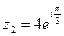 |
9. Запишите в тригонометрической и показательной форме к.ч. а) 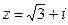 ; б) ; б) 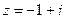 | 9. Запишите в тригонометрической и показательной форме к.ч. а) 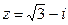 ; б) ; б) 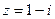 |
Раздел 2. Уравнения и неравенства
Самостоятельная работа № 4.
Графическое решение уравнений и неравенств
Цель: Уметь с помощью графика находить решение уравнений и неравенств.
Изучив тему, письменно ответьте на вопросы:
1. Графическая интерпретация решения уравнения 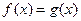 .
.
2. Графическая интерпретация решения неравенства 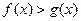 .
.
3. Определение числа корней уравнения 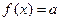 (графическое).
(графическое).
4. Записать решение прим.18, с. 193.
Литература: М.Я. Пратусевич «Алгебра и начала математического анализа» 10кл., М., «Просвещение», 2014, с.193.
Самостоятельная работа № 5.
Иррациональные уравнения. Уравнения и неравенства с модулем
Цель: Знать правила избавления от иррациональности, раскрытия модуля числа и уметь пользоваться ими при решении уравнений и неравенств.
Методические рекомендации
Формулы для повторения:
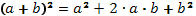 ;
;
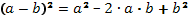 ;
;
Решение квадратных уравнений:
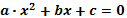
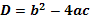 ,
,
Если 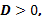 то
то 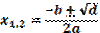
Если 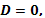 то
то 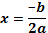
Если 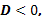 то корней нет
то корней нет
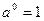 ;
; 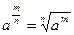 ;
; 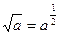 ;
; 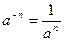 ;
; 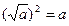 ;
; 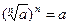
1. Изучив тему, письменно ответьте на вопросы:
10. Введите понятие иррационального уравнения.
20. Сформулируйте утверждение и замечание на с.350.
30. Решение уравнений, содержащих квадратные радикалы.
40. Записать решение примера 60, с. 351.
50. Метод уединения радикалов (прим. 61).
60. Сформулируйте утверждение на с. 352.
70. Дайте определение 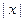 и его иной формы.
и его иной формы.
80. Таблица решения элементарных уравнений и неравенств с модулем.
90. Записать решение примера 85, с. 74.
100. Запишите вывод о решении неравенства с модулем.
110. Запишите решение примера 90, с. 76.
2. Выполните письменно задания:
| 1 вариант | 2 вариант |
1. Решите уравнения: а) 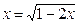 ; б) ; б) 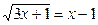 ; в) ; в) 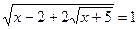 . . | 1. Решите уравнения: а) 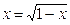 ; б) ; б) 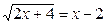 ; в) ; в) 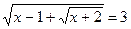 . . |
2. Решите уравнения: а) 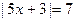 ; б) ; б) 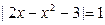 . . | 2. Решите уравнения: а) 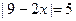 ; б) ; б) 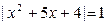 . . |
3. Решите неравенства: а) 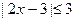 ; б) ; б) 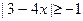 . . | 3. Решите неравенства: а) 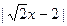 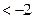 ; б) ; б) 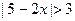 . . |
Литература: М.Я. Пратусевич «Алгебра и начала анализа», 10кл., М., «Просвещение» 2014, гл. I, §10; 11кл.-гл.XIII, §84.
Самостоятельная работа № 7.
Решение заданий на преобразование логарифмических выражений
Цель: Знать основное логарифмическое тождество, свойства логарифмов, уметь применять их при преобразовании выражений.
Методические рекомендации
I. Свойства логарифмов.
1.Основное логарифмическое тождество: 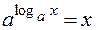
2. 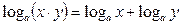
3. 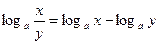
4. 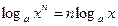
5. 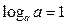
6. 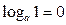
7. 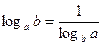
8. 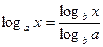 - формула перехода к другому основанию
- формула перехода к другому основанию
9. 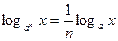
Используя методические рекомендации, выполните задания:
| 1 вариант | 2 вариант |
1. Найдите значение числового выражения: 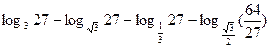 | 1. Найдите значение числового выражения: 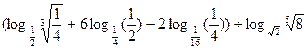 |
2. Вычислите: а) 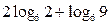 ; б) ; б) 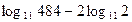 ; в) ; в) 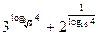 | 2. Вычислите: а) 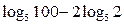 ; б) ; б) 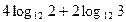 ; в) ; в) 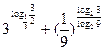 |
3. Найдите 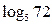 , если известно, что , если известно, что 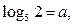 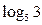 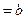 . . | 3. Вычислите 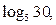 если известно, что если известно, что 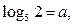 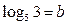 . . |
4. Вычислить: а) 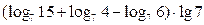 ; б) ; б) 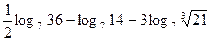 | 4. Вычислить: а) 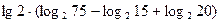 ; б) ; б) 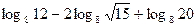 |
Самостоятельная работа № 8.
