Действия над комплексными числами
Суммой двух комплексных чисел 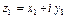 и
и 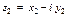 называется комплексное число, определяемое равенством
называется комплексное число, определяемое равенством
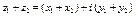 .
.
Разностью двух комплексных чисел 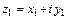 и
и 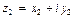 называется комплексное число, вычисленное по формуле
называется комплексное число, вычисленное по формуле
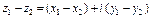 . (6)
. (6)
Пример 2.Найти сумму и разность комплексных чисел 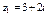 и
и 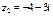 .
.
Решение.Чтобы найти сумму комплексных чисел, необходимо сложить соответственно их действительные и мнимые части:
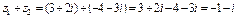 .
.
Вычитание комплексных чисел выполняется аналогично сложению:
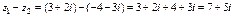 .
.
Ответ. 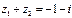 ,
, 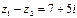 .
.
Произведением комплексных чисел 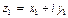 и
и 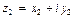 называется комплексное число, определяемое равенством
называется комплексное число, определяемое равенством
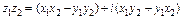 . (7)
. (7)
То есть, чтобы найти произведение комплексных чисел, необходимо умножить их по правилу умножения двучленов, помня что i2 = -1 .
Проиллюстрируем умножение комплексных чисел на следующем примере:
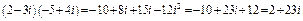 .
.
Следует отметить, что произведение комплексного числа z на сопряженное число 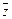 равно действительному числу
равно действительному числу
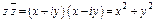 . (8)
. (8)
При умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются
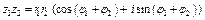 . (9)
. (9)
Возведение комплексных чисел в степеньnвыполняют по формуле Муавра
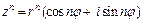 . (10)
. (10)
Пример 3.Вычислить 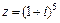 .
.
Решение. Обозначим выражение, стоящее в основании степени, через z1
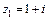 .
.
Найдем модуль и аргумент числа z1:
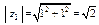 ,
, 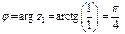 .
.
Вычислим значение 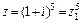 по формуле (10):
по формуле (10):
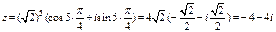 .
.
Ответ. 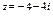 .
.
Правило деления. Чтобы разделить число z1 на число z2 необходимо числитель и знаменатель дроби 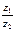 умножить на число
умножить на число 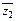 , сопряженное знаменателю.
, сопряженное знаменателю.
Пример 4. Найти частное от деления чисел 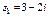 и
и 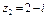 .
.
Решение.
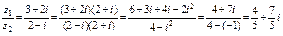 .
.
Ответ. 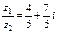 .
.
Извлечение корней n-ой степени из комплексных чисел определяется как действие, обратное возведению в степень.
Корнемn-ой степени из комплексного числа z называется комплексное число 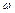 , удовлетворяющее равенству
, удовлетворяющее равенству 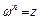 , т. е.
, т. е. 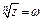 .
.
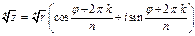 , где
, где 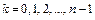 . (11)
. (11)
Замечание. Рассмотренная задача извлечения корня n-ой степени из комплексного числа равносильна решению уравнения вида 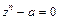 , где, очевидно,
, где, очевидно, 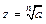 . Для решения уравнения нужно найти n значений
. Для решения уравнения нужно найти n значений 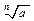 , а для этого необходимо найти модуль и аргумент комплексного числа и использовать формулу извлечения корня.
, а для этого необходимо найти модуль и аргумент комплексного числа и использовать формулу извлечения корня.
Пример 5. Решить уравнение 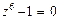 .
.
Решение.Преобразуем исходное уравнение 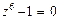 :
:
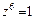 ,
,
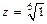 .
.
Примем подкоренное выражение за комплексное число z1= 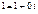 .
.
Определим модуль и аргумент числа z1:
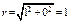 ,
, 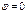 .
.
Полученные значения 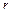 и
и 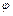 подставим в формулу (11):
подставим в формулу (11):
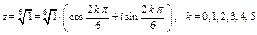 .
.
Заметим, что справа стоит 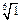 - арифметический корень, его единственное значение равно 1.
- арифметический корень, его единственное значение равно 1.
Придавая 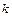 последовательно значения от 0 до 5 , выписываем все возможные решения уравнения:
последовательно значения от 0 до 5 , выписываем все возможные решения уравнения:
если 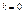 , то
, то 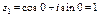 ,
,
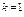 , то
, то 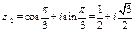 ,
,
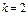 , то
, то 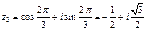 ,
,
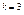 , то
, то 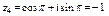 ,
,
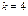 , то
, то 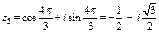 ,
,
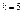 , то
, то 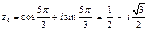 .
.
Ответ.Уравнение имеет шесть корней:
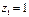 ,
, 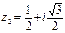 ,
, 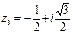 ,
, 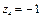 ,
, 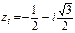 ,
, 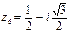 .
.
Пример 6.Дано комплексное число 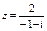 . Требуется:
. Требуется:
а) записать число z в алгебраической и тригонометрической формах;
б) найти все корни уравнения 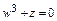 .
.
Решение.
а) чтобы получить алгебраическую форму числа z, умножим его числитель и знаменатель на число, сопряженное знаменателю
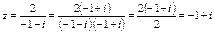 .
.
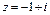 - это алгебраическая форма числа z.
- это алгебраическая форма числа z.
Для записи числа z в тригонометрической форме вычислим | z | и arg z:
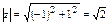 ,
, 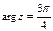 .
.
Тригонометрическая форма числа z:
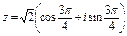 .
.
б) запишем уравнение 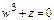 в виде
в виде 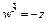 , откуда
, откуда 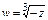 .
.
Представим число - z в тригонометрической форме
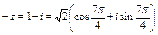 .
.
Корни уравнения вычислим по формуле (11)
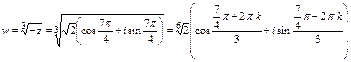 .
.
При к = 0 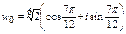 ,
,
к = 1 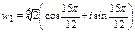 ,
,
к = 2 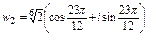 .
.
Ответ.а) алгебраическая форма числа z: 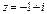 , тригонометрическая форма числа z:
, тригонометрическая форма числа z: 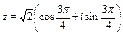 ,
,
б) уравнение имеет три корня:
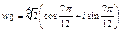 ,
, 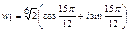 ,
, 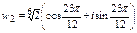 .
.
