П. 2. Задачи, приводящие к дифференциальным уравнениям

Задача 1. Материальная точка массы m замедляет свое движение под действием силы сопротивления среды, пропорциональной квадрату скорости V. Найти зависимость скорости времени. Найти скорость точки через 3 с после начала замедления, если V(0) = 100 м/с, а V(1) = 50 м/с.

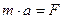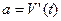Решение. Примем за независимую переменную время t, отсчитываемое от начала замедления движения материальной точки. Тогда скорость точки V будет функцией t, т.е. V = V(t). Для нахождения V(t) воспользуемся вторым законом Ньютона (основным законом механики): , где – есть ускорение движущегося тела, F – результирующая сила, действующая на тело в процессе движения.

В данном случае 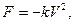k › 0 – коэффициент пропорциональности (знак минус указывает на то, что скорость тела уменьшается). Следовательно, функция V = V(t) является решением ДУ 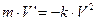или 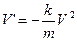. Здесь m – масса тела.

Откуда находим, что 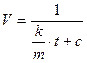, где с – const. Найдя зависимость скорости от времени, легко найти скорость точки через 3 с после начала замедления.

Найдем сначала параметры 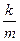и с. Согласно условию задачи, имеем: 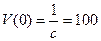и 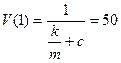. Отсюда 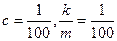. Следовательно, скорость точки изменяется по закону 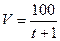. Поэтому V(3) = 25 m/c.

Задача 2. Найти кривую, проходящую через точку (4; 1), зная, что отрезок любой касательной к ней, заключенный между осями координат, делится в точке касания пополам.

Решение. Пусть M(x; y) – произвольная точка кривой, уравнение которой y = f(x). Для определенности предположим, что кривая расположена в первой четверти (рис. 1).

Для составления ДУ воспользуемся геометрическим смыслом первой производной: tg α есть угловой коэффициент касательной; в точке M(x; y) он равен y’, т.е. y’ = tg α.

Из рисунка видно, что tg( 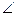MBC) = 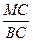. Но tg( 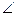MBC) = tg(180⁰ – α)=

= - tg α, MC = y. По условию задачи AM = MB, следовательно, ОС = СВ = = x.

Таким образом, получаем - tg α= 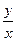или 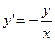. Решением полученного ДУ является функция 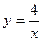(гипербола).

Дифференциальные уравнения первого порядка

П. 1. Основные понятия

ДУ первого порядка в общем случае можно записать в виде 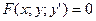(1).

Уравнение связывает независимую переменную x, искомую функцию y и ее производную y’. Если уравнение (1) можно разрешить относительно y’, то его записывают в виде y’ = f(x; y) (2) и называют ДУ первого порядка, разрешенным относительно производной.

Уравнение (2) устанавливает связь (зависимость) между координатами точки (x; y) и угловым коэффициентом y’ касательной к интегральной кривой, проходящей через эту точку. Следовательно, ДУ y’ = f(x; y) дает совокупность направлений (поле направлений) на плоскости Oxy. Таково геометрическоеистолкование ДУ первого порядка.

Кривая, во всех точках которой направление поля одинаково, называется изоклиной. Изоклинами можно пользоваться для приближенного построения интегральных кривых. Уравнение изоклины можно получить, если положить y’ = c, т.е. f(x; y) = c.

ДУ первого порядка, разрешенное относительно производной, можно записать в дифференциальной форме: 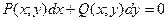(3), где P(x; y) и Q(x; y) – известные функции. Уравнение (3) удобно тем, что переменные x и y в нем равноправны, т.е. любую из них можно рассматривать как функцию другой. Отметим, что от одного вида записи ДУ можно перейти к другому.

Интегрирование ДУ в общем виде приводит к бесконечному множеству решений (отличающихся друг от друга постоянными величинами).

Чтобы решение ДУ приобрело конкретный смысл, его надо подчинить некоторым дополнительным условиям.

Условие, что при x = x₀ функция y должна быть равна заданному числу y₀, т.е. y = y₀ называется начальным условием. Начальное условие записывается в виде y(x₀) = y₀ (4).

Определение 1. Общим решением ДУ первого порядка называется функция y = φ(x; c), содержащая одну произвольную постоянную и удовлетворяющая условиям:

1. Функция φ(x; c) является решением ДУ при каждом фиксированном значении с.

2. Каково вы ни было начальное условие (4), можно найти такое значение постоянной с = с₀, что функция y = φ(x; c₀) удовлетворяет начальному условию.

Определение 2. Частным решением ДУ первого порядка называется любая функция y = φ(x; c₀), полученная из общего решения y = φ(x; c) при конкретном значении постоянной с = с₀.

Если общее решение ДУ найдено в неявном виде, т.е. в идее уравнения Φ (x; y; c) = 0, то такое решение называется общим интегралом ДУ. Уравнение Φ (x; y; c₀) = 0 в этом случае называется частным интегралом уравнения.

С геометрической точки зрения y = φ(x; c) есть семейство интегральных кривых на плоскости Oxy; частное решение y = φ(x; c₀) – одна кривая из этого семейства, проходящая через точку (x₀; y₀).

Определение 3.Задача отыскания решения ДУ первого порядка (3), удовлетворяющего заданному начальному условию (4), называется задачей Коши.

Теорема (существования и единственности решения задачи Коши). Если в уравнении (2) функция f(x; y) и ее частная производная f’_y(x; y) непрерывны в некоторой области D, содержащей точку (x₀; y₀), то существует единственное решение y = φ этого уравнения, удовлетворяющее начальному условию (4).

Геометрический смысл теоремы состоит в том, что при выполнении ее условий существует единственная интегральная кривая ДУ, проходящая через точку (x₀; y₀).