Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения первого порядка. Изоклины. Задача Коши. Теорема существования и единственности задачи Коши.

Уравнения, в которые неизвестная функция входит под знаком производной или дифференциала, называются дифференциальными уравнениями. Подобными уравнениями описываются многие физические явления и процессы.

Примеры.

1) 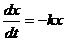- уравнение радиоактивного распада ( k – постоянная распада, х – количество неразложившегося вещества в момент времени t, скорость распада 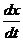пропорциональна количеству распадающегося вещества).

2) 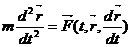- уравнение движения точки массы т под влиянием силы F, зависящей от времени, положения точки, определяемого радиус-вектором r, и ее скорости 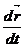. Сила равна произведению массы на ускорение.

3) 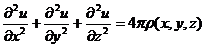- уравнение Пуассона, задающее зависимость между многими физическими величинами. Например, можно считать, что u(x,y,z) – потенциал электростатического поля, а ρ(x,y,z) – плотность зарядов.

Мы будем рассматривать уравнения, где неизвестная функция является функцией одной переменной. Такие уравнения называются обыкновенными дифференциальными уравнениями.

Определение 16.1. Уравнение вида

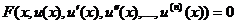(16.1)

называется обыкновенным дифференциальным уравнением п-го порядка. При этом порядком уравнения называется максимальный порядок входящей в него производной.

Определение 16.2. Функция, которая при подстановке в уравнение (16.1) обращает его в тождество, называется решениемдифференциального уравнения.

Дифференциальные уравнения первого порядка, разрешенные

Относительно производной.

Рассмотрим уравнение вида 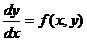. (16.2)

Можно показать, что общее решение такого уравнения зависит от одной произвольной постоянной. С геометрической точки зрения уравнение (16.2) устанавливает зависимость между координатами точки на плоскости и угловым коэффициентом 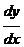касательной к графику решения в той же точке. Следовательно, уравнение (16.2) определяет некоторое поле направлений, и задача его решения состоит в том, чтобы найти кривые, называемые интегральными кривыми, направление касательных к которым в каждой точке плоскости совпадает с направлением этого поля.

Примеры.

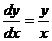1) . В каждой точке, кроме начала координат, угловой коэффициент к искомой интегральной кривой равен 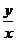, то есть тангенсу угла, образованного с осью Ох прямой, проходящей через данную точку и начало координат. Следовательно, интегральными кривыми в данном случае будут прямые вида у = сх (рис.1).

у

у

х

х

Рис. 1. Рис. 2.

2) 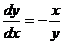. В этом случае касательная в каждой точке плоскости перпендикулярна направлению прямой, проходящей через эту точку и начало координат, так как угловые коэффициенты этих прямых удовлетворяют условию ортогональности: 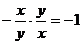. Поэтому направление касательной в данной точке совпадает с направлением касательной к окружности с центром в начале координат, на которой лежит выбранная точка. Такие окружности и являются интегральными кривыми данного уравнения (рис. 2).

Часто для построения интегральных кривых удобно предварительно найти геометрическое место точек, в которых касательные к искомым интегральным кривым сохраняют постоянное направление. Такие линии называются изоклинами.

Пример.

Изоклины уравнения 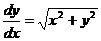задаются уравнениям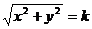и или 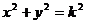, так как на каждой изоклине производная 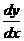должна сохранять постоянное значение. Полученные уравнения задают семейство концентрических окружностей с центром в начале координат, а угловой коэффициент касательной к интегральной кривой равен радиусу проходящей через данную точку окружности.