П.5. Уравнение в полных дифференциалах. Интегрирующий множитель.

Определение 8. Уравнение Р(х;y )∙ dх + Q(x; у) ∙ dу = 0 (1) называется уравнением в полных дифференциалах, если его левая часть полный дифференциал некоторой функции 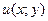, т.е. .

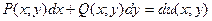В этом случае ДУ (1) можно записать в виде 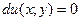, а его общий интеграл будет: .

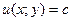Приведем условие, по которому можно судить, что выражение Δ = Р(х;y )∙ dх + Q(x; у) ∙ dу есть полный дифференциал.

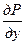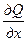Теорема.Для того чтобы выражение Δ = Р(х; y) ∙ dх + Q(x; y) ∙ dу, где функции P(x; y) и Q(x; y) и их частные производные и непрерывны в некоторой области D плоскости Oxy, было полным дифференциалом, необходимо и достаточно выполнение условия 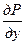= 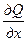(2).

Доказательство:

Необходимость.Пусть Δ есть полный дифференциал, т.е. 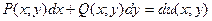. Учитывая, что 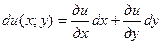, имеем: 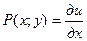, 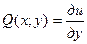. Дифференцируя эти равенства по y и по x соответственно, получаем 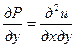и 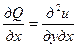. А так как смешанные частные производные 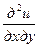и 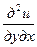равны между собой, получаем формулу (2).

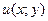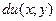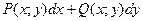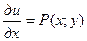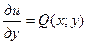Достаточность. Пусть в области D выполняется условие (2). Покажем, что существует функция в области D такая, что = . Найдем эту функцию. Искомая функция должна удовлетворять требованиям: и (3).

Если в первом уравнении (3) зафиксировать y и проинтегрировать его по x, то получим: 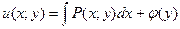(4). Здесь произвольная постоянная 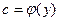зависит от y (либо является числом). В решении (4) не известна лишь φ(y). Для ее нахождения продифференцируем функцию (4) по y: 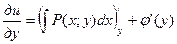. Используя второе равенство (3), можно записать: 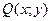= 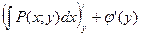. Отсюда 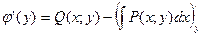(5). В равенстве (5) левая часть зависит от y. Покажем, что и правая часть равенства зависит только от y.

Для этого продифференцируем правую часть по x и убедимся, что производная равна нулю. Действительно, 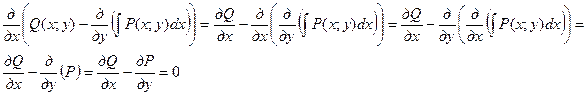в силу условия (2).

Из равенства (5) находим φ(y): 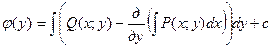, с – const.

Подставляя найденное значение для φ(y) в равенство (4), находим функцию u(x; y). Решение записываем в виде u(x; y)= c.

Таким образом, при решении ДУ вида (1) сначала проверяем выполнение условия (2). Затем, используя равенства (3), находим функцию u(x; y). Решение записываем в виде u(x; y)= c.

П. 6. Уравнения Лагранжа и Клеро

Рассмотрим ДУ, неразрешенные относительно производной. К ним, в частности, относятся уравнения Лагранжа и Клеро.

Уравнение Лагранжа

Определение 9. Уравнение вида 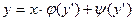(1), где φ и ψ – известные функции от 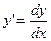, называется уравнением Лагранжа.

Введем вспомогательный параметр, положив y’ = p. Тогда уравнение (1) примет вид 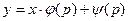(2). Дифференцируя по x, получим: 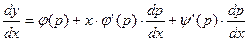, т.е. 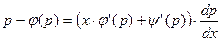или 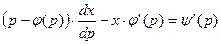(3). Уравнение (3) есть линейное уравнение относительно неизвестной функции x = x(p). Решив его, найдем: x = λ(p; c) (4). Исключая параметр p из уравнений (2) и (4), получаем общий интеграл уравнения (1) в виде y = γ(x; c).

Отметим, что, переходя к уравнению (3), мы делили на 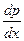. При этом могли быть утеряны решения, для которых 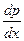=0, т.е. p = p₀ = const. Это значение p₀ является корнем уравнения p – φ(p) = 0.

Решение 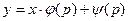является особям решением для уравнения (1).

Уравнение Клеро

Рассмотрим частный случай уравнения Лагранжа при φ(y’) ≡ y’. Уравнение (1) принимает вид 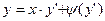(5) и называется уравнением Клеро.

Положив y’ = p, получаем: 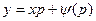(6).

Дифференцируя по x, имеем: 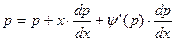, или 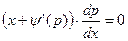. Если 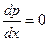, то p = c. Поэтому, с учетом формулы (6) имеем общее решение 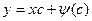(7).

Если 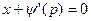, то получаем частное решение уравнения в параметрической форме: 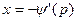, 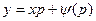. Это решение – особое решение уравнения Клеро: оно не содержится в формуле общего решения уравнения.