Решение обыкновенных дифференциальных уравнений в среде Scilab

Солвер служит для решения обыкновенного дифференциального уравнения (ОДУ)

dy/dt=f(t,y) , y(t0)=y0

Синтаксис

y=ode(y0,t0,t,f)

[y,w,iw]=ode([type],y0,t0,t [,rtol [,atol]],f [,jac] [,w,iw])

[y,rd,w,iw]=ode("root",y0,t0,t [,rtol [,atol]],f [,jac],ng,g [,w,iw])

y=ode("discrete",y0,k0,kvect,f)

Параметры

y0: действительное число или матрица (условия инициализации)

t0: действительный скаляр (время инициализации)

t: действительный вектор. Задает интервал времени для которого вычисляется решение уравнения.

f: внешний параметр (функция или строка или список).

type: строковая переменная принимающая одну из следующих значений: "adams" "stiff" "rk" "rkf" "fix" "discrete" "roots".adams применяют при решении дифференциальных уравнений или систем методом прогноза-коррекции Адамса; stiff указывают при решении жестких задач; rk используют при решении дифференциальных уравнений или систем методом Рунге-Кутта четвертого порядка; rkf указывают при выборе пятиэтапного метода Рунге-Кутта четвертого порядка; fix тот же метод Рунге-Кутта, но с фиксированным шагом;

rtol, atol: действительные константы и действительные константы того же размера, что и y, по умолчанию rtol=0.00001, atol=0.0000001, при использовании параметров rkf и fix - rtol=0.001, atol=0.0001;

jac: матрица, представляющая собой якобиан правой части жесткой системы дифференциальных уравнений, задают матрицу в виде внешней функции вида J=jak(t,y);

w, iw: векторы, предназначенные для сохранения информации о параметрах интегрирования, которые применяют для того, чтобы последующие вычисления выполнялись с теми же параметрами.

ng: целое число.

g: внешний параметр (функция или строка или список).

k0: целое число (начальное время).

kvect: целочисленный вектор.

Листинг

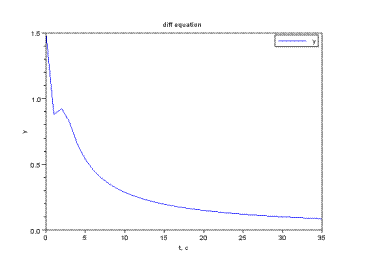
function yd=f(t,x),yd=-x+sin(t*x),endfunction;

x0=1.5;

t0=0;

t=0:1:35;

y=ode(x0,t0,t,f);

plot(t,y)

Листинг

//Функция, описывающая систему дифференциальных уравнений

function dy=syst(t, y)

dy=zeros(2, 1);

dy(1)=cos(y(1)*y(2));

dy(2)=sin(y(1)+y(2)*t);

endfunction

//Решение системы дифференциальных уравнений

x0=[0; 0];

t0=0;

t=0:0.1:10;

y=ode(x0, t0, t, syst);

//Формирование графического решения

plot(t, y)

xtitle('diff equation', 't, c','y')

legend('y')

Листинг

function dx=syst2(t, x) //Функция задающая систему ОДУ

dx=zeros(3, 1);

dx(1)=-7*x(1)+7*x(2);

dx(2)=157*x(1)+x(2)-1.15*x(1)*x(3);

dx(3)=0.96*x(1)*x(2)-8.36*x(3);

endfunction

//Решение ОДУ

x0=[-1;0;1];

t0=0;

t=0:0.01:2;

y=ode("stiff",x0,t0,t,syst2);

plot(t,y);

xgrid();

Листинг

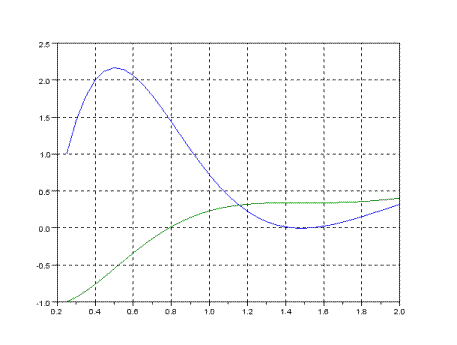
function F=FF(t,x)

F=[-4*x(1)-13*x(2)+exp(t); x(1)];

endfunction

//Решение системы дифференциальных уравнений

X0=[1;-1];

t0=0.25;

t=0.25:0.05:2;

y=ode("stiff",X0,t0,t,FF);

//Вывод графика решения

plot(t,y);

xgrid();

Листинг

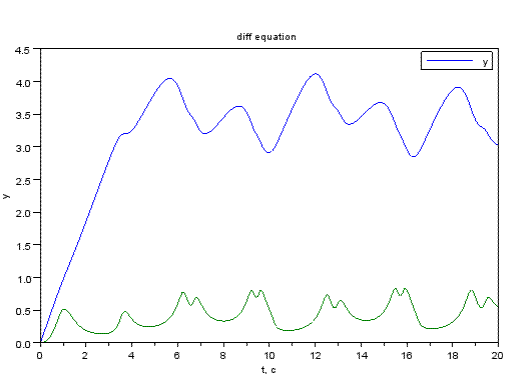
function yy=myfun(t)

yy=5*t*sin(t)*exp(-0.1*t);

endfunction

function dy=syst(t, y)

dy=zeros(2,1);

dy(1)=cos(y(1)*y(2));

dy(2)=sin(y(1)+y(2)*myfun(t));

endfunction

//Решение системы дифференциальных уравнений

clc;

x0=[0;0];

t0=0;

t=0:0.1:20;

y=ode(x0,t0,t,syst);

//Формирование графического решения

plot(t,y)

xtitle('diff equation','t, c','y')

legend('y')

Решение систем линейных алгебраических уравнений

Метод Крамера

Система m уравнений с n неизвестными вида:

- a₁₁x₁ + a₁₂x₂ + ... + a_1nx_n = b₁,

- a₂₁x₁ + a₂₂x₂ + ... + a_2nx_n = b₂,

- . . . . . . . . . . . . . . . . . . . . .

- a_m1x₁ + a_m2x₂ + ... + a_mnx_n = b_m,

называется системой линейных алгебраических уравнений (СЛАУ), причем x_j - неизвестные , a_ij - коэффициенты при неизвестных , b_i - свободные коэффициенты (i=1..m, j=1..n). Система из m линейных уравнений с n неизвестными может быть описана при помощи матриц: A∙x=b, где x - вектор неизвестных, A - матрица коэффициентов при неизвестных или матрица системы, b - вектор свободных членов системы или вектор правых частей . Совокупность всех решений системы (x₁, x₂,..., x_n), называется множеством решений или просто решением системы.

Пример

Решить СЛАУ при помощи правила Крамера:

- 2x₁ + x₂ - 5x₃ + x₄ = 8,

- x₁ - 3x₂ - 6x₄ = 9,

- 2x₂ - x₃ + 2x₄ = -5,

- x₁ + 4x₂ - 7x₃ + 6x₄= 0.

Правило Крамера заключается в следующем. Если определитель Δ=det(A) матрицы системы из n уравнений с n неизвестными A∙x=b отличен от нуля, то система имеет единственное решение x₁, x₂,..., x_n, определяемое по формулам Крамера: x_i=Δ_i/Δ, где Δ_i - определитель матрицы, полученной из матрицы системы А заменой i- го столбца столбцом свободных членов b. Текст файла- сценария с решением задачи по формулам Крамера :

- //Матрица коэффициентов:

- A=[2 1 -5 1;1 -3 0 -6;0 2 -1 2;1 4 -7 6];

- b=[8;9;-5;0]; //Вектор свободных коэффициентов

- A1=A;A1(:,1)=b; //Первая вспомогательная матрица

- A2=A;A2(:,2)=b; //Вторая вспомогательная матрица

- A3=A;A3(:,3)=b; //Третья вспомогательная матрица

- A4=A;A4(:,4)=b; //Четвертая вспомогательная матрица

- D=det(A); //Главный определитель

- //Определители вспомогательных матриц:

- d(1)=det(A1); d(2)=det(A2); d(3)=det(A3); d(4)=det(A4);

- x=d/D //Вектор неизвестных

- P=A*x-b //Проверка

Результаты работы файла-сценария:

- x =

- 3.

- - 4.

- - 1.

- 1.

- P = 1.0D-14 *

- 0.1776357

- 0.

- - 0.0888178

- 0.1554312

- exec done

Метод обратной матрицы:

для системы из n линейных уравнений с n неизвестными A∙x=b, при условии, что определитель матрицы А не равен нулю, единственное решение можно представить в виде x=A^-1∙b.

Текст файла- сценария и результаты его работы :

- //Матрица и вектор свободных коэффициентов системы:

- A=[2 1 -5 1;1 -3 0 -6;0 2 -1 2;1 4 -7 6];b=[8;9;-5;0];

- x=inv(A)*b //Решение системы

//Результаты работы файла-сценария:

- --> x =

- 3.

- - 4.

- - 1.

- 1.

Метод Гаусса

Решение системы линейных уравнений при помощи метода Гаусса основывается на том, что от заданной системы, переходят к эквивалентной системе, которая решается проще, чем исходная система.

Метод Гаусса состоит из двух этапов. Первый этап это прямой ход, в результате которого расширенная матрица6 системы путем элементарных преобразований (перестановка уравнений системы, умножение уравнений на число отличное от нуля и сложение уравнений) приводится к ступенчатому виду. На втором этапе (обратный ход) ступенчатую матрицу преобразовывают так, чтобы в первых n столбцах получилась единичная матрица. Последний, n+1 столбец этой матрицы содержит решение системы линейных уравнений. Далее приведен текст файла-сценария и результаты его работы:

- //Матрица и вектор свободных коэффициентов системы:

- A=[2 -1 1;3 2 -5;1 3 -2]; b=[0;1;4];

- //Приведение расширенной матрицы к треугольному виду:

- C=rref([A b]);

- //Определение размерности расширенной матрицы:

- [n,m]=size(C); //m- номер последнего столбца матрицы С

- //Выделение последнего столбца из матрицы С:

- x=C(:,m) //x - решение системы

//Результаты работы программы:

- --> x =

- 0.4642857

- 1.6785714

- 0.75