Разработка числовой экономико-математической модели задачи

Всю информацию по составлению кормосмеси записывают в матрицу задачи, которая приводится в приложении Е.

Технико-экономическими коэффициентами матрицы задачи являются в основном показатели содержания различных питательных веществ в единице каждого вида корма и кормовой добавки.

В задачу входят 18 ограничений, которые записаны по строкам матрицы.

Первое условие задачи, которое требует того, что бы общий вес всех компонентов кормосмеси был равен 100 граммам. Оно записывается таким образом:

1) x₁+ x₂+ …+x₈ = 100

Следующие пять ограничений задачи обеспечивают содержание в рассчитываемой кормосмеси необходимого количества различных питательных веществ. Так ограничение по содержанию обменной энергии записывается как:

2) 2,6x₁+ 2,6x₂+2,75x₃+2,5x₄+9x₆ >= 245

Аналогичным образом составляются ограничения 3-6.

Каждая группа и вид кормов может изменяться в определенных пределах. Поэтому устанавливаются нижние и верхние границы включения в состав кормосмеси их содержания. В пределах разницы между нижней и верхней границей может изменяться содержание каждой группы и вида корма.

Требования по включению в состав кормосмеси минимально и максимально содержания отдельных групп кормов осуществляется с помощью включения в задачу дополнительных ограничений (7-12).

Так, например, требование по включению в состав кормосмеси не мене 88% концентрированных кормов можно записать следующим образом:

7) 2.6 x₁ + 2,6x₂ >= 215,6

Замечание. Ограничения по включению отдельных групп и видов кормов строятся по балансу обменной энергии (в килокалориях).

В задачу входят дополнительные ограничения по включению отдельных видов кормов в состав кормосмеси. Например, для полного сбалансирования рассчитываемого состава кормосмеси по минимальному содержанию соли вводится ограничение вида:

13) x₇ >= 0,03

Ограничения 14-16 имеют аналогичный характер построения.

Следующая группа ограничений определяет включение отдельных видов кормов в соответствующую группу. Так ограничения 17-18 по включению рыбной муки в группу кормов животного происхождения выглядят так:

17) x₄ >= 0,2(x₃ + x₄) или после преобразования: –0,2x₃ + 0,8x₄ >= 0

18) –0,4x₃ + 0,6x₄ <= 0.

Разработка числовой модели задачи и матрицы оканчивается определением функционала. Целевая функция задачи имеет следующую математическую запись:

С= 0,37х₁ + 0,41х₂ + 0,65х₃ + 2.6х₄ + 0,03х₅ + 1.75х₆ + 0,1х₇ + 0,45х₈ " min

4.5 Решение задачи на ПК

Для решения задачи на ПК можно использовать специализированные программы для решения оптимизационных задач линейного программирования и программы общего назначения. Покажем методику решения экономико-математических моделей задач.

4.5.1 Решение задач по программе LP.SAR

1. Включить ПК.

2. Войти в каталог STAT на диске R:\.

Создание файла данных производят в следующем порядке:

z1 x1 x2 …x8 = 100 [Enter]

z2 2,6x1 2,6x2 2,75x3 2,5x4 9x6 >= 245 [Enter]

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

z18 -0.6x3 0.4x4 <= 0 [Enter]

Целевая функция задачи (Фразу не набираем):

z19 0,37х1 0,41х2 0,65х3 2.6х4 0,03х5 1.75х6 0,1х7 0,45х8

Сохранить файл данных.

Загрузить программу LP.SAR.

На запрос «Введите свою фамилию инициалы» необходимо ввести названное и нажать [Enter].

На запрос «Введите количество основных переменных: N=» вводится число переменных, для нашего примера 8.

На запрос «Будете ли вводить название основных переменных? (Y/N):» необходимо ввести одну их латинских букв. В случае ввода основных переменных Y, в противном случае N.

Замечание. Если экономико-математическая модель задачи решается в первый раз, то нецелесообразно вводить имена основных переменных, только после отладки модели задачи и получения оптимального решения следует вводить эти данные.

На запрос «Введите количество условий-ограничений М=» ввести количество ограничений без учета ограничений по неотрицательности переменны и целевой функции задачи, и нажать [Enter].

На запрос «Введите имя текстового файла с данными» ввести имя файла.

Далее выдается контроль размеров задачи, т.е. программа определяет правильность ввода количества переменных и ограничений в исходном файле задачи. Если это условие выполняется, то здесь же производится запрос «Критерий оптимальности? 1(max), 0(min)». Если задача решается на максимум, то необходимо ввести 1, а на минимум – 0.

Результат решения задачи будет записан в файле, имя которого такое же, как и файла данных, однако расширение файла будет .res. Для нашего примера korma.res. (см. приложение Ж).

Если система ограничений задачи несовместна, то в файле с расширением .res будет показана «Промежуточное решение». В этом случае необходимо загрузить текстовый файл (в нашем случае korma.txt) и произвести корректировку экономико-математической модели задачи, а затем вновь решить задачу.

Если после решения задачи файл с расширением .res не образован, тогда это говорит о том, что целевая функция задачи неограниченна. Требуется корректировка экономико-математической модели задачи.

4.5.2 Решение задачи по программе «Поиск решения»

Прежде чем воспользоваться программой Поиск решения необходимо создать файл данных. Файл данных создается в электронных таблицах Excel.

Фрагмент электронной таблицы с исходными данными оптимизационной задачи представим в приложении И. Необходимо уточнить следующее. В ячейках С4:J4 должны быть поставлены нули – это изменяющиеся ячейки. Здесь в результате решений будут находиться значения искомых переменных величин.

В ячейке К5:К22 необходимо ввести формулы. Например, для ячейки К5 формула выглядит следующим образом:

=(C5*C4+D5*D4+E5*E4+F5*F4+G5*G4+H5*H4+I5*I4+J5*J4),

а для ячейки К22:

=(E22*E4+F22*F4).

Целевая ячейка М23 содержит формулу:

=(C23*C4+D23*D4+E23*E4+F23*F4+G23*G4+H23*H4+I23*I4+J23*J4).

В этой ячейке будет находиться минимальное значение целевой функции.

После того, как создан файл данных можно приступать к решению задачи с помощью программы Поиск решения.

Программа Поиск решений является дополнительной, то есть при инсталляции пакета MS Office она могла быть не установлена, перед ее активизацией обратитесь к команде [Надстройки] меню [Сервис] приложения Excel. На экране появится одноименное диалоговое окно, в котором можно проверить, доступна ли эта программа.

Проверьте, установлено ли в списке надстроек опция программы Поиск решения. Если да, то, по идее, соответствующая программа должна быть доступна при открытии меню [Сервис]. Если же в списке надстроек нет даже элемента Поиск решения, то с помощью кнопки [Обзор] Вам представляется возможность предпринять необходимые шаги по ее установке.

Если все в порядке, можно активизировать программу Поиск решения. На экране откроется одно диалоговое окно.

В диалоговом окне Поиск решения необходимо задать ряд параметров (рис.1). В поле [Установить целевую ячейку] следует указать адрес ячейки, содержимое которой должно быть оптимизировано. В нашем случае это ячейка М23, в которой представлена минимум стоимости кормосмеси. Очень важно, чтобы эта ячейка содержала формулу и была хотя бы косвенно связана с влияющими ячейками, иначе при изменении одной ячейки не будет изменяться другие. Поскольку в нашем примере необходимо минимизировать значения в целевой ячейке, выделите в группе опций [Равной] опцию [Минимальному значению]. В поле [Изменяя ячейки] необходимо задать область ячеек, значения которых программа должна заменить для получения оптимального результата. Активизируйте указанное поле ввода и выделите ячейки C4:J4 (в случае необходимости переместите диалоговое окно или укажите адрес области вручную).

Примечание. При нажатии кнопки [Предположить] Excel выделяет область ячеек, на которых прямо или косвенно ссылается целевая ячейка.

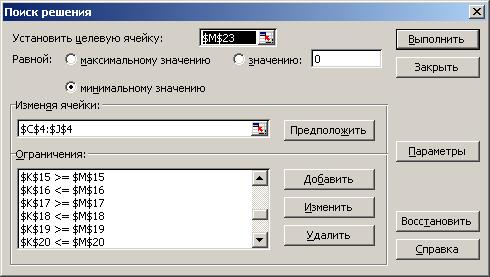
Рис.1. Окно Поиск решения

Теперь следует приступить к заданию ограничений, играющих немаловажную роль. Ограничения могут применяться к зависимым, влияющим или другим ячейкам, прямо или косвенно связанным с целевой ячейкой. Заданные ограничения следует указать в одноименном поле диалогового окна Поиск решения.

Чтобы задать ограничения, нажмите кнопку [Добавить], после чего на экране появится диалоговое окно, в котором можно выполнить все необходимые установки (рис.2).

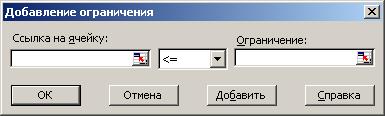
Рис. 2. Окно Добавление ограничений

В поле [Ссылка на ячейку] этого диалогового окна следует указать адрес ячейки, содержимое которой должно удовлетворять заданному ограничению. В поле необходимо задать значения или адрес ячейки, если требуемое значение содержится в определенной ячейке. Содержимое указанных полей соединяется с помощью известных Вам операторов сравнения.

После ввода ограничений необходимо нажать кнопку ОК, при этом диалоговое окно задания ограничений будет закрытым. Тем самым все параметры для запуска программы Поиск решения заданы. При необходимости, используя кнопку [Изменить], Вы сможете в дальнейшем изменить заданные ограничения. После нажатия кнопки [Удалить] выделенное ограничение будет удалено из списка. Чтобы можно было без особых проблем несколько раз последовательно повторить поиск оптимального значения для одной и той же целевой ячейки с измененными параметрами, записи в диалоговом окне Поиск решения сохраняются. При следующем вызове программы Поиск решения необходимо изменить только желаемый параметр. Вышесказанное имеет силу только во время одного сеанса работы с программой и при работе только с текущей рабочей книгой. При сохранении рабочей книги после применения программы Поиск решения параметры, установленные в диалоговом окне Поиск решения, также будут сохранены. В дальнейшем после открытия данной рабочей книги и активизации программы Поиск решения все параметры снова будут представлены на экране.

Запустите процесс вычисления нажатием кнопки [Выполнить] и следите за строкой состояния. В ней отображаются отдельные шаги выполнения операции поиска решения. После завершения вычислений новые значения будут вставлены в таблицу, а на экране появится диалоговое окно, информирующее о завершении процесса поиска решения (рис.3).

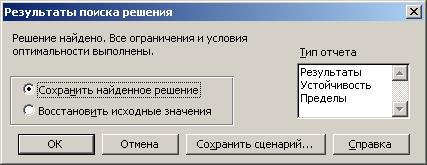
Рис. 3. Окно результатов поиска решения

В ней программа представляет Вам свободу выбора. Полученный результат можно отразить в текущей рабочей книге или представить в виде отчета. Отчет создается на отдельном рабочем листе. При задании режима создания отчета в списке [Тип отчета] следует выбрать [Тип отчета]. Если активизирована опция [Сохранить найденное решение], то после закрытия диалогового окна нажатием кнопки [ОК], новые значения будут представлены в текущей таблице, приложение К.

Если поиск решения успешно закончен, в окне диалога [Результаты поиска решения] выводится одно из следующих сообщений:

· Решение найдено. Все ограничения и условия оптимальности выполнены.

· Все ограничения соблюдены с установленной точностью и найдено заданное значение целевой ячейки.

· Поиск свелся к текущему решению. Все ограничения выполнены.

· Значение целевой ячейки, не менялось в течение последних пяти итераций. Решение возможно найдено или итеративный процесс улучшает решение очень медленно.

Если поиск не способен достичь оптимального решения, в окне диалога [Результаты поиска решения] выводится одно из следующих сообщений:

· Поиск не может улучшить текущее решение. Все ограничения выполнены.

· Поиск остановлен (истекло заданное на поиск время).

· Поиск остановлен (достигнуто максимальное число итераций).

· Значение целевой ячейки не сходятся.

· Поиск не может найти подходящего решения.

· Поиск остановлен по требованию пользователя.

· Условия для линейной модели не удовлетворяются.

· При поиске решения обнаружено ошибочное значение в целевой ячейке или в ячейке ограничения.

· Мало памяти для решения задачи.

4.6 Анализ результатов решения задачи

Анализ результатов решения задачи производят двумя способами: традиционным и с помощью двойственных оценок. Традиционный способ решения задачи предусматривает сравнение фактического состав кормосмеси с оптимальным составом. Для анализа оптимального плана можно использовать следующие таблицы:

Таблица 1 – Фактический и оптимальный состав кормосмеси, г (фрагмент)

Виды кормов	Факт	Оптимальный план	Оптимальный план к факту, %
Комбикорм		31,78	37,4
………………………………...	…	…	…
Мясокостная мука		3,56	118,7
………………………………...	…	…	…
Сода	0,03	0,03	100,0
Всего	100,0	100,0	100,0

Необходимо дать сравнительную характеристику питательной ценности фактического и оптимального состава кормосмеси., таблица 2.

Таблица 2 – Сравнительная характеристика фактического и оптимального состава кормосмеси (фрагмент)

Компоненты	Факт	Оптимальный план
г	Обменная энергия, ккал.	…	Натрий	г	Обменная энергия, ккал.	…	Натрий
Комбикорм				0,052	31,78	82,63		0,019
……………………	…	…	…	…	…	…	…	…
Мясокостная мука		8,25	…	0,051	3,56	9,79	…	0,060
…………………….	…	…	…	…	…	…	…	…
Сода	0,03	-	…	0,069	0,03	-	…	0,0069
Всего	100,0	245,0	…	0,40	100,0	245,0	…	0,40

Необходимо сравнить стоимость фактического и оптимального состава кормосмеси, таблица 3.

Таблица 3 – Сравнительная характеристика стоимости фактического и оптимального состава кормосмеси

Компоненты	Стоимость 1 г, коп. .	Факт	Оптимальный план
Количество, г	Стоимость, всего, коп.	% к итогу	Количество, г	Стоимость, всего, коп.	% к итогу
Комбикорм	0,37		31,5	72,10	31,78	11,76	28,90
……………………	…	…	…	…	…	…	..
Мясокостная мука	0,65		2,0	4,60	3,56	2,31	5,68
…………………….	…	…		…	…	…
Сода	0,45	0,03	0,02	0,04	0,03	0,01	0,02
Всего	-	100,0	43,7	100,0	100,0	40,65	100,0

Наиболее важным является выявить экономическую эффективность предлагаемого варианта кормосмеси, таблица 4.

Таблица 4 – Сравнительная эффективность фактического и оптимального вариантов кормосмеси для кур-несушек

Показатели	Факт	Оптимальный план	Оптимальный план к факту, %
Стоимость 100г состава кормосмеси, коп.	43,7	40,65	93,0
Содержание в кормосмеси обменной энергии, ккал.			100,0
Стоимость 1 ккал., коп.	0,17	0,16	94,1
Расход кормосмеси на 1000 голов в сутки, г	Нет. свед.	Нет. свед.	Нет. свед.
Стоимость кормов на 1000 голов в сутки, руб.	Нет. свед.	Нет. свед.	Нет. свед.
Экономия в затратах на корма на 1000 голов, руб.	Нет. свед.	Нет. свед.	Нет. свед.
Экономия в затратах на корма на все поголовье, тыс. руб.	Нет. свед.	Нет. свед.	Нет. свед.

Двойственные оценки позволяют определить эффективность или невыгодность использования того или иного вида ресурса.

Двойственные оценки основных переменных, не вошедших в оптимальный план, характеризуют количественную меру «неэффективности». Их следует расценивать так: если соответствующую переменную ввести в план в размере равной единице измерения, то критерий оптимальности уменьшится на величину оценки (если задача решается на максимум или наоборот).

Для ограничений типа «меньше-равно» двойственные оценки, отличные от нуля с качественной стороны указывают на то, что данное ограничение решено по верхней границе. В том случае, когда ограничение имеет отношение к использованию ресурсов, это значит, что данный вид ресурсов дефицитен, используется он полностью и увеличение его объема всегда экономически целесообразно. Количественная величина самой оценки в этом случае выражает величину «чистого эффекта» от увеличения данного ресурса на единицу, т.е. насколько увеличится значений критерия оптимальности. Например, для нашей задачи восьмое ограничение по максимальному содержанию концентрированных кормов решено по верхней границе. Двойственная оценка данного ограничения равна 0,064. Это означает, что введение в состав кормосмеси одного грамма концентрированных кормов увеличивает стоимость кормосмеси на 0,064 копейки. Нулевая оценка свидетельствует о том, что данный вид ресурсов не используется полностью и при увеличении его объема значение критерия оптимальности не изменится.

Ненулевые оценки ограничений типа «больше-равно» указывают, что данное ограничение решено по нижней границе. Производство данного вида продукции или кормов неэффективно. Величина оценки в данном случае показывает, насколько уменьшится значение критерия оптимальности, если нижнюю границу объема ограничения поднять на единицу и наоборот. Например, ограничение по содержанию обменной энергии имеет двойственную оценку 0,191. Если величину обменной энергии увеличить на одну килокалорию, то значение целевой функции увеличится на 0,191 копейку. Нулевые оценки указывают на то, что данные производства эффективны и вошли в план с превышением, т.е. имеет место перевыполнение плана.

ПРИЛОЖЕНИЯ

Приложение А

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РФ

Департамент научно-технологической политики и образования

ФГОУ ВПО КОСТРОМСКАЯ ГОСУДАРСТВЕННАЯ СЕЛЬСКОХОЗЯЙСТВЕННАЯ АКАДЕМИЯ