Метод интегрирования по частям

В основе этого метода лежит такая теорема.

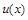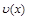Теорема 2. Если функции и определены и дифференцируемы на промежуткеХи на этом промежутке существует первообразная функции 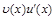, тогда на промежуткеХсуществует также первообразная функции 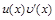и выполняется равенство

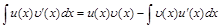.(3)

Формула (3) называется формулой интегрирования по частям в неопределенном интеграле.

Поскольку 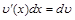и 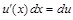, ее можно записать также в виде

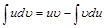. (4)

Эта формула дает возможность свести нахождение интеграла 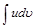к нахождению интеграла 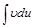, который может оказаться более простым, чем исходный.

Пример 7.Для нахождения интеграла 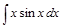положим 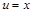, , 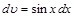тогда 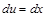, , 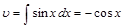и, согласно формуле (4) имеем

.

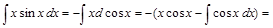
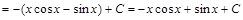Классы функций, которые интегрируются по частям

І.В интегралах вида

, , , ,

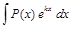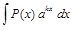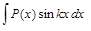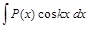где 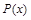– многочлен, k – число, целесообразно обозначить 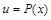, а оставшуюся часть подинтегрального выражения – .

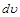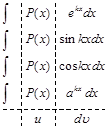
Пример 8.

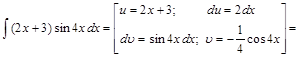
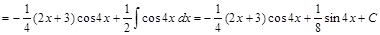
Пример 9.

.

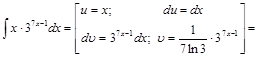
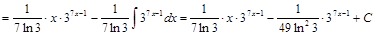ІІ.В интегралах вида

, , , ,

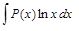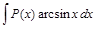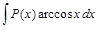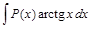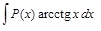
целесообразно обозначить 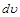= 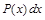, а оставшуюся часть подинтегрального выражения – .

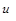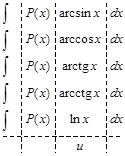
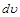
Пример 10.

.

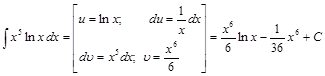Пример 4.

.

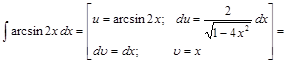
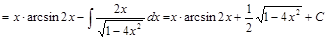ІІІ. В интегралах вида

, ,

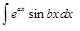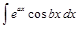где а и b — числа, за 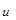принимается функция .

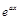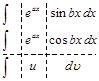
Интегрирование рациональных дробей

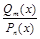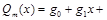Определение 1. Дробно-рациональной функциейилирациональной дробьюназывается частное двух многочленов , где и 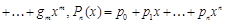– многочлены степени т и п, причем .

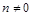Определение 2.Рациональная дробь 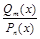называется правильной, если высший показатель степени числителя т меньше соответствующей степени п знаменателя .

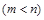Определение 3.Дробь называется неправильной, если .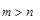

Любую неправильную рациональную дробь 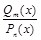можно, разделив числитель на знаменатель, изобразить в виде суммы многочлена 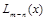и правильной рациональной дроби :

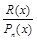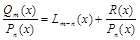.(1)

Пример 1. 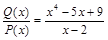– неправильная рациональная дробь. Разделим числитель на знаменатель столбиком:

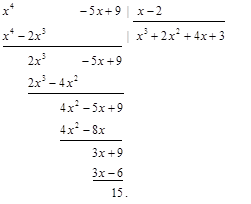
Имеем:

.

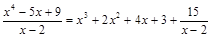Поскольку интегрирование целой части 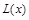довольно простое, достаточно научиться интегрировать правильные дроби.

Интегрирование правильных рациональных дробей

Определение 4.Дроби вида

І. ;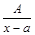

ІІ. 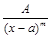, где 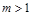, целое;

ІІІ. 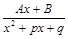, где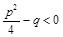

(трехчлен 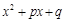не имеет действительных корней);

ІV. 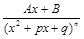, где 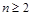, целое,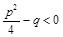

(трехчлен 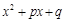не имеет действительных корней);

где 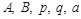– действительные числа, 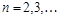, называются простейшими (элементарными) рациональными дробями І, ІІ, ІІІ и ІV типа.

Дальше будет показано, что любую рациональную дробь можно представить в виде суммы простейших дробей.

Интегралы от простейших рациональных дробей І и ІІ типов находят методом непосредственного интегрирования:

І. 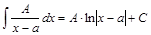; (2)

ІІ.

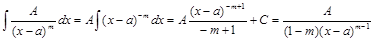+С.(3)

Пример 2.Найти интеграл .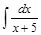

Решение. .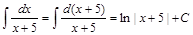

Пример 3.Найти интеграл .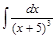

Решение.

.

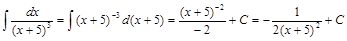Пример 4.Найти интеграл .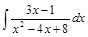

Решение.

.

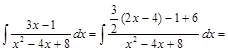
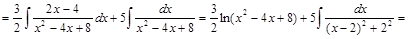
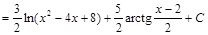Интегрирование рациональной дроби 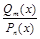сводится к интегрированию простых дробей с помощью следующей важной теоремы алгебры.

Теорема 1. Каждая правильная дробь 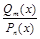, 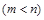может быть представлена в виде суммы конечного числа простых дробей.

Возможны следующие случаи:

1) корни знаменателя действительные и разные, т.е.

.

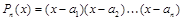В этом случае дробь 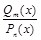раскладывается в сумму простейших дробей I типа:

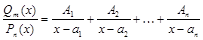(4)

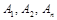находятся с тождества (4).

2) корни знаменателя действительные, причем некоторые из них кратные, т.е. .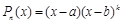

В этом случае дробь 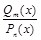раскладывается в сумму простейших дробей I и II типа:

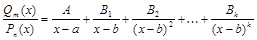. (5)

Коэффициенты 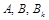находятся с тождества (5).

3) корни знаменателя действительные, причем некоторые из них кратные, кроме того знаменатель содержит квадратный трехчлен, не имеющий действительных корней.

В этом случае дробь 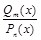раскладывается в сумму простейших дробей I, II, III типов:

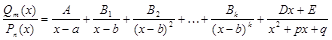, (6)

где коэффициенты 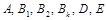находятся с тождества (6).

Пример 5.Найти .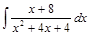

Решение. Уравнение 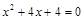имеет кратный корень 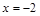, поэтому

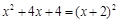і.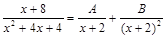

Сведя правую часть последнего равенства к общему знаменателю, получим 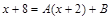. Тогда

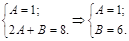
Итак,

.

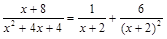Поэтому

.

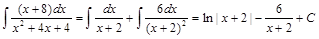Пример 6.Найти .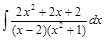

Решение. Разложим подинтегральную дробь на простые дроби:

.

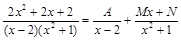Получим

.

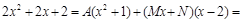
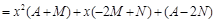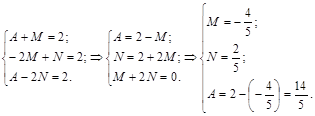
Тогда

.

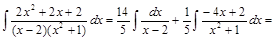
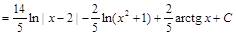Пример 7.Найти интеграл .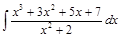

Решение.Выделим целую часть данной неправильной рациональной дроби, разделив числитель на знаменатель:

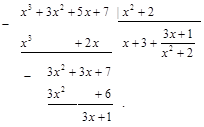
Итак,

.

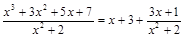Отсюда находим

.

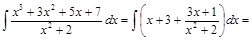
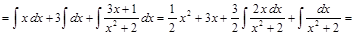
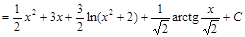Пример 8. Вычислить интеграл:

.
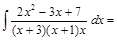
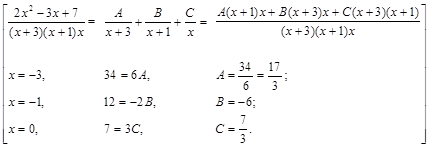
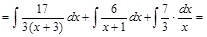
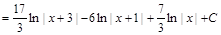