III. Метод интегрирования по частям

Методы интегрирования

Для вычисления интеграла мы должны привести его к табличному интегралу и таким образом найти искомый результат. Рассмотрим наиболее часто встречающиеся приемы интегрирования и покажем их применение на примерах.

Наиболее важными методами интегрирования являются:

1) метод непосредственного интегрирования (метод разложения),

2) метод подстановки (метод замены переменной),

3) метод интегрирования по частям.

Рассмотрим данные методы сначала для неопределенных интегралов.

I. Метод непосредственного интегрирования

Задача нахождения неопределенных интегралов от многих функций решается методом сведения их к одному из табличных интегралов.

Пример 1. Найти .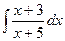

Выполним преобразования и перейдем к табличным интегралам:

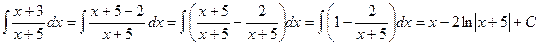
II. Метод подстановки (метод замены переменной)

Если функция 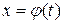имеет непрерывную производную, то в данном неопределенном интеграле 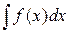всегда можно перейти к новой переменной t по формуле

.

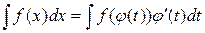Затем найти интеграл из правой части и вернуться к исходной переменной. При этом интеграл, стоящий в правой части данного равенства может оказаться проще интеграла, стоящего в левой части этого равенства, или даже табличным. Такой способ нахождения интеграла называется методом замены переменной.

Пример 2. .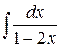

Положим 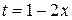. Тогда , .

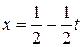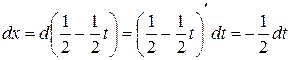Подставляем в исходный интеграл, вычисляем и возвращаемся к исходной переменной:

.

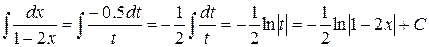Отметим, что новую переменную можно не выписывать явно (т.е. ввести переменную под знак дифференциала)

Пример 3. Найти .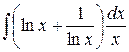

Так как 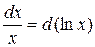, то имеем

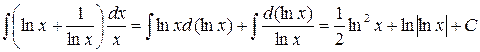
Пример 4.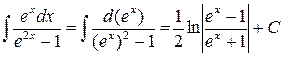

III. Метод интегрирования по частям

Метод интегрирования по частям основан на следующей формуле:

,

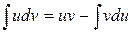где 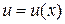, 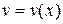–непрерывно дифференцируемые функции.

Формула называется формулой интегрирования по частям для неопределенного интеграла. Возможности применения связаны с тем, что дифференцирование может существенно упростить один из сомножителей.

Пример 5. Найти неопределенный интеграл .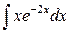

Так как 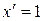, а функция 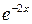при интегрировании практически не изменяется, то данный интеграл можно найти интегрированием по частям, пологая , .

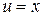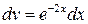Тогда 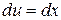, 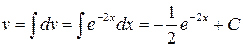. Следовательно, по формуле имеем:

.

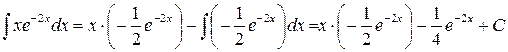Перейдем к рассмотрению метода подстановки (метод замены переменной) для определенных интегралов.

Если функция 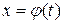имеет непрерывную производную на отрезке 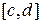, , 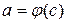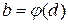и функция 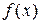непрерывна в каждой точке 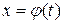, где .

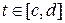Тогда справедливо следующее равенство:

.

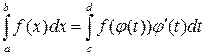Эта формула носит название формулы замены переменной в определенном интеграле.

В данном случае, в отличие от неопределенного интеграла, нет необходимости возвращаться к исходной переменной интегрирования. Достаточно лишь найти пределы интегрирования 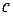и 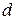по новой переменной t. Для этого, выполняя замену переменной, начинают с того, что указывают выражение t=ψ(х) новой переменной через старую. В этом случае нахождение пределов интегрирования по переменной t упрощается: c=ψ(a), d=ψ(b).

Пример 6. Вычислить .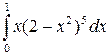

Положим 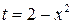. Тогда 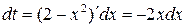и .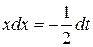

Если х=0, то t=2-0²=2, и если х=1, то t=2-1²=1. Следовательно:

.

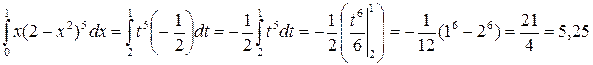Рассмотрим метод интегрирования по частям для определенного интеграла.

Пусть функции 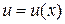, 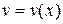имеют непрерывные производные на отрезке [а,b]. Тогда

,

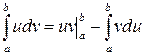где .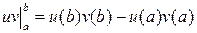

Эта формула называется формулой интегрирования по частям для определенного интеграла.

Пример 7. Вычислить .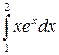

Положим 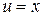, , 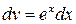отсюда 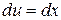, 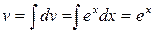и по формуле имеем:

.
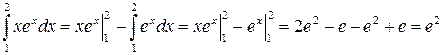