Метод интегрирования по частям

Техника интегрирования

Методические указания и варианты заданий

Барнаул 2010

УДК 517 (075)

Э.И. Вингисаар, Е.В. Колбина Техника интегрирования: методические указания и варианты заданий. – Алт. гос. техн. ун – т им. И.И. Ползунова. – Барнаул: АлтГТУ, 2010. – с. 105

Данная работа содержит большое число интегралов, разнообразных как по различным методам интегрирования, так и по сложности. Знаком «*» отмечены интегралы повышенной сложности.

Методические указания можно использовать для самостоятельной работы студентов, так как в них приведены примеры вычисления многих интегралов и дан достаточный справочный материал.

Из интегралов, содержащихся в индивидуальных заданиях можно формировать расчетные работы разной степени сложности в зависимости от программы специальности и уровня подготовленности студентов. Можно так же проводить контрольные опросы, указав отдельные пункты заданий.

Рекомендовано к изданию на заседании

кафедры высшей математики АлтГТУ

Протокол № 3 от 11.11.2010 г.

Рецензент – доцент Кантор Е.И.

Оглавление

1. Непосредственное интегрирование…………………………...
2. Метод подведения под знак дифференциала………………...
3. Метод замены переменной……………………………………..
4. Метод интегрирования по частям…………………………….
5. Интегрирование некоторых выражений, содержащих квадратный трехчлен……………………………………………
6. Интегрирование рациональных функций…………………...
7. Интегрирование тригонометрических функций……………
8. Тригонометрические подстановки……………………………
9. Интегрирование иррациональных функций. ……………….
10. Подстановки Эйлера…………………………………………...
11. Приложения…………………………………………………….
12. Типовые расчеты………………………………………………

Непосредственное интегрирование

1)

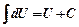
2)

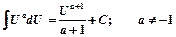
3)

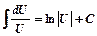
4)

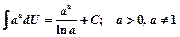
5)

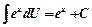
6)

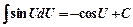
7)

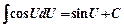
8)

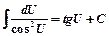
9)

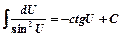
10)

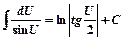
11)

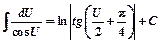
12)

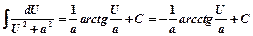
13)

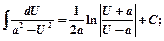
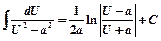
14)

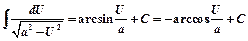
15)

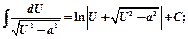
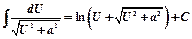
16)

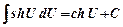
17)

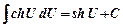
18)

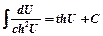
19)

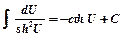
Свойства линейности неопределенного интеграла:

1)

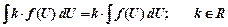
2)

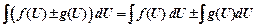
Метод подведения под знак дифференциала

Этот метод часто используется для сведения данного интеграла к табличному или более простому и применяется в тех случаях, когда подынтегральное выражение содержит какую-либо функцию и ее производную.

Для использования метода подведения под знак дифференциала необходимо знать:

1) свойства дифференциала

а)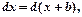

б)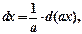

в)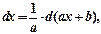

где а, b – некоторые действительные числа.

2) свойства неопределенного интеграла

а) ,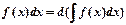

б) 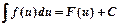, где .

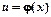3) таблицу производных.

4) таблицу интегралов.

Пример 1.

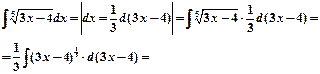
Далее можно использовать один из вариантов решения.

1 вариант:

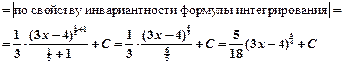
2 вариант:

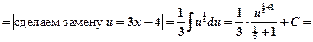
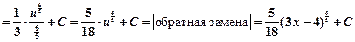
Пример 2.

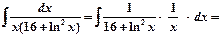
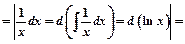
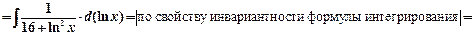
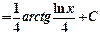
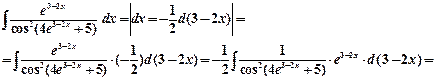
Пример 3.

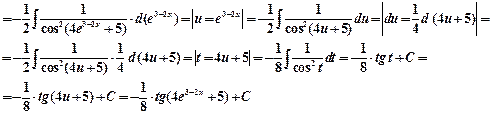
Метод замены переменной

Если 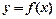непрерывна и функция 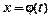непрерывна вместе со своей производной, то справедлива формула .

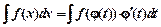Правило подстановки.

Чтобы вычислить интеграл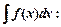

а) заменяем 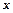какой-нибудь обратимой функцией 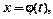находим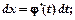

б) вычисляем полученный интеграл;

в) в найденном ответе производим обратную замену 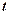на .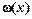

Пример 1.

.

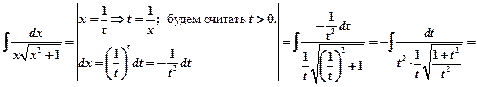
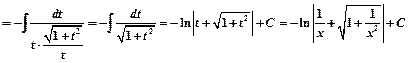Пример 2.

.

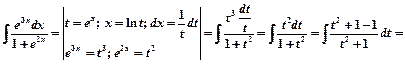
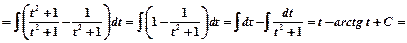
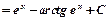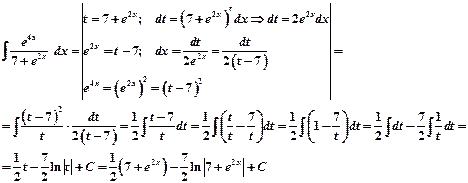
Пример 3.

Пример 4.

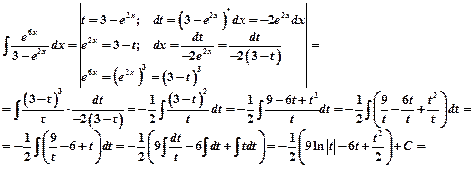
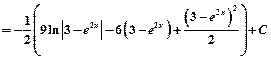
Пример 5.

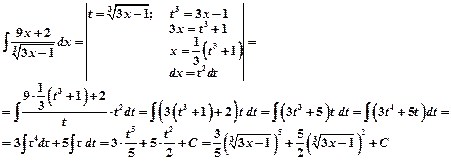
Замечание: подбирать выгодные подстановки можно научиться тренировкой. Существуют стандартные подстановки для некоторых типов интегралов.

Интегралы вида:

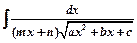и 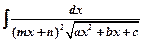легко интегрируются подстановкой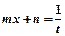

Пример 6.

.

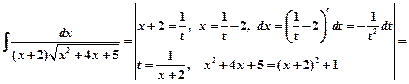
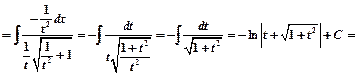
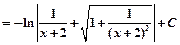Пример 7.

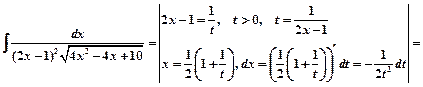
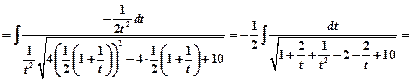
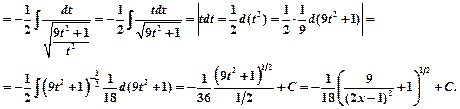
Метод интегрирования по частям

Пусть 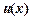и 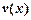- непрерывно дифференцируемые функции, тогда имеет место равенство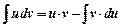

Эта формула называется формулой интегрирования по частям. Ее смысл состоит в том, что нахождение интеграла 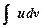сводится к отыскания другого интеграла 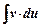, который либо проще исходного, либо подобен ему. Иногда интегрирование по частям приходится применять несколько раз в одной задаче.

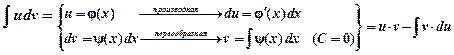
Чтобы не ошибиться в составлении правой части формулы, используйте схему:

Перечислим некоторые типы интегралов, в которых следует применять метод интегрирования по частям.

I тип

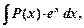
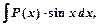
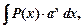
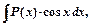
где 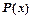- многочлен,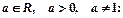

в схеме: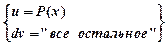

Пример 1.

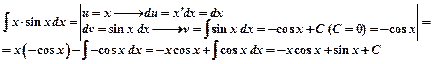
Пример 2.

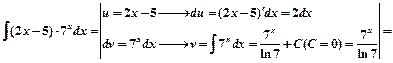
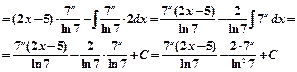
II тип

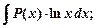
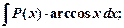
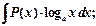
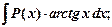
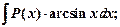
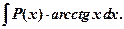
где 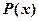- многочлен,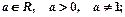

в схеме: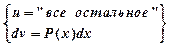

Пример 3.

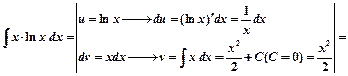
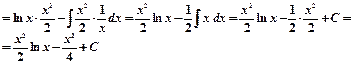
Пример 4.

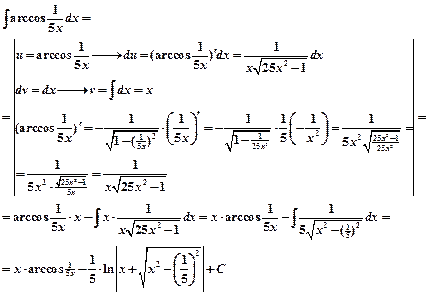
III тип(Особые, так называемые «циклические» интегралы)

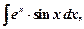
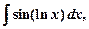
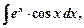
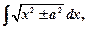
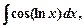
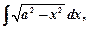и т.д.,

где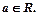

Алгоритм решения

1) Применить формулу интегрирования по частям один или два раза, пока не получится интеграл, такой же как данный;

2) этот интеграл обозначить за I;

3) решить полученное уравнение относительно неизвестной I;

4) в конце выражения приплюсовать константу С.

Пример 5.

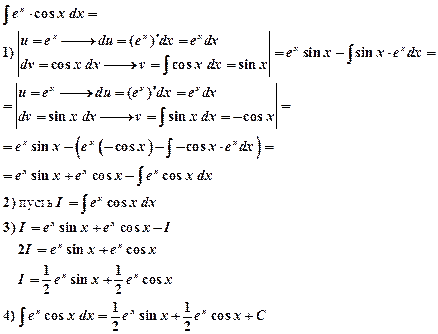
Пример 6.

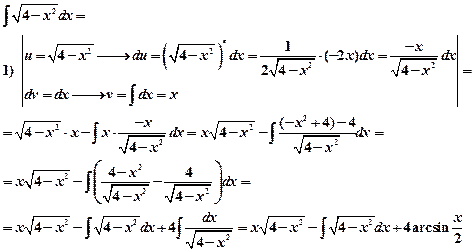
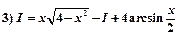
2) пусть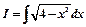

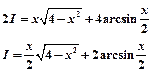
4) .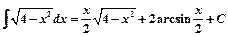