Контрольного ДОМАШНего Задания № 1

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

По выполнению

КонтрольнЫх ДОМАШНИх Заданий

На САМОСТОЯТЕЛЬНУЮ работу СТУДЕНТОВ

по дисциплине «Статистические методы контроля качества технических систем»

для студентов электротехнического факультета

Составитель – доц. Кравцов П.Г.

Самара 2013

Задание 1.Для выполнения задания № 1 рекомендуется использовать следующие теоретические сведения.

Задача 1. Тема «Формула полной вероятности».

События образуют полную группу, если хотя бы одно из них обязательно произойдет в результате эксперимента.

Предположим, что событие A может наступить только вместе с одним из нескольких попарно несовместных событий H1, H2, ... ,Hn, образующих полную группу. Будем называть события Hi(i = 1, 2, … , n) гипотезами. Вероятность появления события А определяется по формуле полной вероятности:

n

å

H H H H

P(A)=i=1P(Hi)×Pi(A)=P(H1)×P1(A)+P(H2)×P2(A)+...+P(Hn)×Pn(A).

Задача 2. Тема «Формула Бернулли».

Если производится несколько независимых испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимыми относительно события А.

Пусть производится n независимых одинаковых испытаний (опытов, экспериментов), в каждом из которых возможны только два исхода:

1) событие А наступило, что происходит с вероятностью p;

2) событие А не наступило, что происходит с вероятностью q = 1 – p.

Требуется определить вероятность того, что при проведении n испытаний событие A появится ровно m раз.

Для решения этой задачи используется формула Бернулли

,

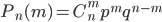где число сочетаний из n элементов по m

.

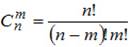Примечание. По определению, 0! = 1.

Задание 2. Для выполнения задания № 2 рекомендуется использовать следующие теоретические сведения.

Задача 3. Тема «Числовые характеристики случайных величин».

Числа, которые обобщенно описывают случайную величину, называются числовыми характеристиками случайной величины. К числу важных числовых характеристик относятся: математическое ожидание, дисперсия, среднее квадратическое отклонение.

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности, т.е.

å

i i

M(X)= n xp.i=1

Дисперсией дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

é ù é ù

D(X)=MëX-M(X)û2=M(X2)-ëM(X)û2.

Средним квадратическим отклонением случайной величины X называют квадратный корень из дисперсии:

s(X)=D(X).

ОФОРМЛЕНИЕ ОТЧЕТОВ

1. Результаты выполнения самостоятельной работы по контрольным заданиям оформляются в виде отдельных отчетов по каждому заданию на листах формата А4.

2. Допускаются как рукописный вариант оформления, так и компьютерный набор отчета (шрифт 16, межстрочный интервал – 1,5).

3. Содержание отчетов должно соответствовать выданным вариантам контрольных домашних заданий, а листы каждого из отчетов должны быть либо сброшюрованы и скреплены степлером, либо сложены в отдельный файл.

4. Примеры оформления отчетов о результатах выполнения самостоятельной работы приведены в Приложениях 1 и 2.

Приложение 1

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования

«Самарский государственный технический университет»

Кафедра «Электропривод и промышленная автоматика»

ОТЧЕТ О ВЫПОЛНЕНИИ

контрольного ДОМАШНего Задания № 1