Операции над последовательностями
1. Образование последовательности
Последовательность T, состоящую из элементов e1,…,en, представляют в виде T(e1,…,en). В частности, при n=0 последовательность T() называют пустой.
2. Выборка элементов последовательности
Если x – последовательность, то ее элементы можно записать следующим образом:
А) x[i] – i-й элемент;
Б) first(x) – первый элемент;
В) last(x) – последний элемент.
3. Включение и исключение элементов последовательности
А) tail(x) – образование последовательности, исключая из x первый элемент;
Б) initail(x); – образование последовательности, исключая из x последний элемент;
В) appendl(x,e) – образование последовательности с добавлением элемента e слева;
Г) appendr(x,e) – образование последовательности с добавлением элемента e справа.
Например, если последовательность x состоит из элементов e1,…,en, то:
tail(x) = T(e2,…,en)
initail(x) = T(e1,…,en-1)
appendl(x,e) = T(e,e1,…,en)
appendr(x,e) = T(e1,…,en,e)
first(appendl(x,e)) = e
tail(appendl(x,e)) = x
appendl(tail(x),first(x)) = x; при x<>T()
last(appendr(x,e)) = e
initail(appendr(x,e)) = x
appendr(initail(x),last(x)) = x; при x<>T()
Последовательный файл
Последовательным файлом называется последовательность, для которой определены следующие операции:
1) образование пустой последовательности;
2) first(x) – получение первого элемента последовательности;
3) tail(x) – образование последовательности, исключая из x первый элемент;
4) appendr(x,e) – образование последовательности с добавлением элемента e справа.
Другими словами, последовательный файл представляет собой последовательность элементов, которая допускает выборку начального элемента последовательности и добавление элементов в ее конец. Такие последовательности реализуются на внешней запоминающей среде, например, ленте. Причем запись возможна только в одном направлении. Обработка файла реализуется путем введения файловой переменной f, а также дополнительной переменной типа T0 (T0 – тип компонентов файла), которая называется буферной переменной. Совокупность значений компонентов файла и положение буферной переменной определяют текущее состояние файла:
| f | e1 | e2 | … | ei | … | en-1 | en |
| fl | fr |
fl и fr служат для указания уже просмотренной и еще не просмотренной части файла. С их помощью текущее состояние файла можно задать в виде (fl, fr).
Файл с прямым доступом
Запоминающие устройства типа магнитного диска обычно содержат некоторое количество дорожек, каждая из которых представляет собой запоминающее устройство с последовательным доступом, но которое слишком мало для того, чтобы вместить целый файл или сегмент. Естественно, что указатель на начало такой минипоследовательности служит маркером сегмента для адресации дорожек, с которых начинаются сегменты, и обозначением длины сегмента, может использоваться индексированная таблица. Такие файлы называются индексированными или файлами с прямым доступом. Системы, реализующие файлы с прямым доступом, позволяют выборочно изменять компоненты в середине файла.
Пример:
T1 = TEXT; { - последовательный доступ }
T2 = FILE OF <TYPE>; { - прямой доступ }
Стек
Стек – это последовательность, для которой определены следующие операции:
1) образование пустой последовательности;
2) first(x) – top; – получение первого элемента последовательности;
3) tail(x) – pop; – образование последовательности, исключая из x первый элемент;
4) appendl(x,e) – push; – образование последовательности с добавлением элемента e слева;
5) empty(x) – проверка на пустую последовательность.
Стек (рис. 3.1) – широко используемый тип данных, применяемый, например, для анализа языковых конструкций. Для стека добавление и извлечение элементов возможно только с одного конца последовательности, называющегося вершиной стека (слева). Таким образом, последний добавленный элемент извлекается из стека первым. Поэтому говорят, что стек – это структура с дисциплиной обслуживания «последним пришел – первым ушел» (LiFo).
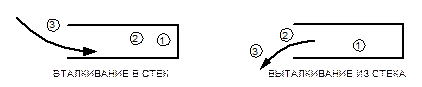
Рис. 3.1. Стек
Стек в программах реализуют на основе вектора (массива) или односвязного линейного списка. В первом случае кроме массива нужно хранить указатель (индекс) вершины стека. Во втором варианте реализации добавление и удаление элемента осуществляются в начале списка.
Примеры
1. Рассмотрим математическое выражение с несколькими уровнями вложенных скобок. Необходимо удостовериться, что скобки расставлены правильно (следует проверить {[( = )]} ). Поэтому все открывающие скобки помещаем в стек, а когда встретится закрывающая, на верхушке стека должна открываться ей парная. После окончания проверки стек должен оказаться пустым.
2. Вычисление алгебраических выражений в постфиксной записи
После чтения очередного операнда он записывается в стек. Когда читается операция, то из стека извлекаются два последних операнда и к ним применяется операция. Результат помещается опять в стек.
ПОКА входная строка не пуста
Symb := следующий символ;
ЕСЛИ Symb = операнд
ТО appendl(x, Symb)
ИНАЧЕ SecondOper := tail(x);
FirstOper := tail(x);
Value := FirstOper (Symb) SecondOper;
appendl(x, Value);
3. Преобразование инфиксной записи в постфиксную с помощью алгоритма Дейкстры
Каждой операции ставится в соответствие некоторый приоритет, а именно: сложение, вычитание – 2, умножение, деление – 3, возведение в степень – 4. Для преобразования используется стек операций.
а. Проверяется очередной символ.
б. Если это операнд, то он передается в выходную строку.
в. Если это открывающая скобка, то она заносится в стек с приоритетом 0.
г. Если это операция, то ее приоритет сравнивается с приоритетом операции в вершине стека. Если приоритет выше, то операция заносится в стек, иначе из стека берется операция и помещается в выходную строку. Процесс сравнения повторяется до тех пор, пока стек не станет пустым или не будет найдена операция с более низким приоритетом. После этого текущая операция заносится в стек.
д. Если текущий символ во входной строке – закрывающая скобка, то операции из стека последовательно переносятся в выходную строку до тех пор, пока на вершине стека не появится открывающая скобка. Эта скобка отбрасывается.
е. Если выражение закончилось, то из стека последовательно переносятся в выходную строку все оставшиеся в нем операции.
Очередь
Очередь – это последовательность, для которой определены следующие операции:
1) образование пустой последовательности;
2) last(x) – получение последнего элемента последовательности;
3) initail(x) – образование последовательности, исключая из x последний элемент;
4) appendl(x,e) – образование последовательности с добавлением элемента e слева;
5) empty(x) – проверка на пустую последовательность.
Часто очередь (рис. 3.2) называют матрицей ожидания. Добавление в очередь осуществляется с левого конца, выборка – с правого. Очередь – это структура с дисциплиной обслуживания «первым пришел – первым ушел» (FiFo – “First input First output”).
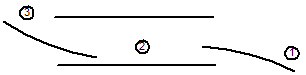
Рис. 3.2. Очередь
Часто очередь реализуют на базе вектора, т.е. одномерного массива. Но в силу его ограниченности рано или поздно может наступить такое состояние, что дальнейшее наращивание невозможно, хотя в массиве еще много свободного места. Поэтому очередь реализуется на базе циклического вектора, который позволяет избежать массовых операций, зависящих от количества элементов в очереди. Использование циклического вектора означает, что при достижении конца массива данные в очередь начинают заноситься в освобожденное в его начале место. Например, если в очереди находятся числа 1, 2, 3, 4, 5, 6, 7, а в массиве зарезервировано место для десяти чисел, то хранение очереди в массиве может быть следующим:
| <пусто> | <пусто> | <пусто> | |||||||
| Правый конец очереди | Левый конец очереди |
Кроме того, очередь можно реализовать на основе односвязного линейного списка. При этом нужно иметь два указателя на начало и конец списка, добавление элемента осуществлять в конец списка, а удаление – из его начала.
Пример. Нахождение одного из кратчайших путей в лабиринте.
| X | |||
 <1> | X | <8> | |
| X | |||
1. Помечается исходная клетка значением 1.
2. Каждая новая помеченная клетка помещается в очередь.
3. Из очереди производится выборка клетки, все ее не помеченные соседки помечаются числом, большим на единицу.
4. Продолжаем шаги 2, 3 пока очередь не будет пуста или не будет достигнута клетка назначения.
5. Если очередь пуста, а последняя выбранная из очереди клетка – не клетка назначения, то пути не существует, иначе путь строится последовательным соединением клеток, начиная с клетки назначения с убыванием значения предыдущей клетки на единицу.
Дек
Дек– это последовательность, для которой определены следующие операции:
1) образование пустой последовательности;
2) appendl(x,e) – образование последовательности с добавлением элемента e слева;
3) appendr(x,e) – образование последовательности с добавлением элемента e справа;
4) tail(x) – образование последовательности, исключая из x первый элемент;
5) initail(x) – образование последовательности, исключая из x последний элемент;
6) first(x) – получение первого элемента последовательности;
7) last(x) – получение последнего элемента последовательности;
8) empty(x) – проверка на пустую последовательность.
Дек – это «гибрид» очереди и стека, в нем очередь движется как вправо, так и влево (рис. 3.3). Поэтому дек еще называют двусторонней очередью (Double Ended Queue).
Рис. 3.3. Дек
В программах дек реализуют либо на основе циклического вектора, либо на основе двусвязного линейного списка.
АЛГОРИТМЫ СОРТИРОВОК
Под сортировкой понимают процесс перестановки объектов данного множества в определенном порядке. Цель сортировки – ускорить последующий поиск элементов в отсортированном множестве. В этом смысле элементы сортировки присутствуют почти во всех задачах. Упорядоченные объекты содержатся в телефонных книгах, в оглавлениях, в библиотеках, в словарях, да и почти всюду, где их нужно разыскивать.
Следовательно, методы сортировки очень важны, особенно при обработке данных. С сортировкой связаны многие фундаментальные приемы построения алгоритмов, выполняющих одну и ту же задачу, многие из которых в некотором смысле являются оптимальными, а большинство имеет какие-либо преимущества по сравнению с остальными.
Зависимость выбора алгоритмов от структуры данных сильна. Методы сортировки обычно разделяют на две категории: сортировка массивов и сортировка файлов. Эти два класса часто называют внутренней и внешней сортировкой, так как массивы располагаются во «внутренней» (оперативной) памяти ЭВМ (для этой памяти характерен быстрый произвольный доступ), а файлы хранятся в более медленной, но более вместительной «внешней» памяти, т.е. на запоминающем устройстве с механическим передвижением (дисках, лентах).
Основные критерии эффективности алгоритмов сортировки следующие:
· быстродействие;
· экономия памяти;
· сокращение времени, затрачиваемого программистом, на реализацию алгоритма.
Поэтому в зависимости от количества элементов множества, их упорядоченности, частоты применения сортировки и других факторов следует использовать различные алгоритмы сортировки.
Для определения эффективности алгоритма будем оценивать числа С – необходимых сравнений ключей и М – присваиваний элементов. Эти числа определяются некоторыми формулами от числа n сортируемых элементов. Хорошие алгоритмы сортировки требуют порядка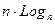 
сравнений.
Сортировка массивов
Введем некоторую терминологию: нам даны элементы – a1, a2, …, an. Сортировка означает перестановку этих элементов в таком порядке: ak1, ak2, …, akn, что при заданной функции упорядочения f справедливо отношение f(ak1)<=f(ak2)<=…<=f(akn).
Обычно функция упорядочения не вычисляется по какому-нибудь правилу, а содержится в каждом элементе в виде явной компоненты (поля). Ее значение называют ключом элемента. Для представления элемента ai будем использовать запись:
type item = record
key: integer;
{описание других компонент}
end;
Прочие компоненты – это все существенные данные об элементе, поле key служит лишь для идентификации элементов. Однако, когда мы говорим об алгоритмах сортировки, ключ – единственная существенная компонента, и нет необходимости выделять все остальные.
Сортировка называется устойчивой, если записи с одинаковыми ключами остаются в прежнем порядке.
Сортировка вставками
Этот метод обычно используют игроки в карты. Элементы (карты) условно разделяются на готовую последовательность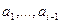 
и входную последовательность 
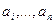. На каждом шаге, начиная с I = 2 и увеличивая i на единицу, берут i-й элемент входной последовательности и передают в готовую последовательность, вставляя его на подходящее место.
| Начальные ключи | ||||||||
| I=2 | ||||||||
| I=3 | ||||||||
| I=4 | ||||||||
| I=5 | ||||||||
| I=6 | ||||||||
| I=7 | ||||||||
| I=8 |
При поиске подходящего места удобно чередовать сравнения и пересылки, т.е. как бы «просеивать» x, сравнивая его с очередным элементом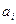 
и либо вставляя x, либо пересылая 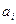направо и продвигаясь налево. «Просеивание» может закончиться при двух различных условиях:
1. Найденный элемент 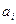с ключом меньшим, чем ключ x.
2. Достигнут левый конец готовой последовательности.
Этот типичный пример цикла с двумя условиями окончания дает нам возможность рассмотреть хорошо известный прием фиктивного элемента («барьера»). Его можно легко применить в этом случае, установив барьер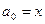 
.
Procedure Sortinsert;
Var i,j : index;
x : item;
Begin
For i:=2 to n do Begin
x:=a[i]; a[0]:=x; j:=i-1;
While x.key < a[j].key do Begin
a[j+1]:=a[j];
j:=j-1;
End;
a[j+1]:=x;
End;
End;
Анализ сортировки простыми включениями. Число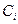 
сравнений ключей при i-м просеивании составляет самое большее i-1, самое меньшее 1 и, если предположить, что все перестановки n ключей равновероятны, в среднем равно i/2. Число 
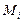пересылок (присваиваний) равно 
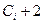(учитывая барьер). Поэтому общее число сравнений и пересылок есть:
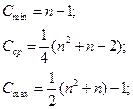
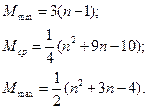
Наименьшие числа появляются, если элементы с самого начала упорядочены, а наихудший случай встречается, если элементы расположены в обратном порядке. В этом смысле сортировка включениями демонстрирует вполне естественное поведение. Ясно так же, что данный алгоритм описывает устойчивую сортировку: он оставляет неизменным порядок элементов с одинаковыми ключами.
Алгоритм сортировки простыми включениями легко можно улучшить, пользуясь тем, что готовая последовательность, в которую нужно включить новый элемент, уже упорядочена. Поэтому место включения можно найти значительно быстрее. Очевидно, что здесь можно применить бинарный поиск, который исследует средний элемент готовой последовательности и продолжает деление пополам, пока не будет найдено место включения. Модифицированный алгоритм сортировки называется сортировкой бинарными включениями.
procedure binaryinsertion;
var i,j,l,r,m : index;
x : item;
begin
for i:= 2 to n do begin
x:= a[i];
i := 1;
r := i - 1;
while l <= r do begin
m := (l+r) div 2;
if x.key < a[m].key then r:=m - 1
else l := m+1
end;
for j := i - 1 downto l do a[j+1] :=a [j];
a[l] := x;
end;
end;
Анализ сортировки бинарными включениями. Количество сравнений не зависит от исходного порядка элементов. Но из-за округления при делении интервала поиска пополам действительное число сравнений для i элементов может быть на 1 больше ожидаемого. Природа этого «перекоса» такова, что в результате места включения в нижней части находятся в среднем несколько быстрее, чем в верхней части. Это дает преимущество в тех случаях, когда элементы изначально далеки от правильного порядка. На самом же деле минимальное число сравнений требуется, если элементы вначале расположены в обратном порядке, а максимальное – если они уже упорядочены. Следовательно, это случай неестественного поведения алгоритма сортировки
С = n (Log(n) – Log(e) ± 0,5).
К сожалению, улучшение, которое мы получаем, используя метод бинарного поиска, касается только числа сравнений, а не числа необходимых пересылок. В действительности, поскольку пересылка элементов, т.е. ключей и сопутствующей информации, обычно требует значительно больше времени, чем сравнение двух ключей, то это улучшение ни в коей мере не является решающим: важный показатель М по-прежнему остается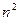 
. И в самом деле, пересортировка уже рассортированного массива занимает больше времени, чем при сортировке простыми вставками с последовательным поиском! Лучших результатов можно ожидать от метода, при котором пересылки элементов выполняются только для отдельных элементов и на большие расстояния. Эта мысль приводит к сортировке выбором.