Операции над логическими последовательностями

Пусть числовая последовательность системы логических функций задана в виде выражения (2.2).

Рассмотрим операции над числовыми последовательностями. Их можно разделить на две группы:

1) операции над аргументами логических функций;

2) операции над самими функциями.

В начале рассмотрим выполнение операций первой группы.

2.2.1. Операция подстановки значения «0» вместо аргумента с весом .

В результате подстановки какого-либо определённого числового значения одного из аргументов системы логических функций 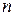аргументов мы получаем систему функций 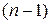-го аргумента. При этом длина числовой последовательности, соответствующей новой системе функций сокращается вдвое, и её длинна будет равна .

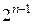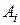Утверждение 2.1. Подставить значение «0» вместо аргумента, имеющего вес , – это значит выбрать из последовательности (2.2) такие , для которых двоичное представление индекса 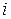имеет ноль в разряде с весом .

Доказательство. При последовательном увеличении значения индекса 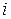, начиная с нуля, мы будем иметь в последовательности (2.2) сначала чисел с нулевым значением разряда с весом в двоичном представлении, затем – чисел с единичным значением. Затем в интересующем нас разряде опять будет нулей и так далее. Таким образом, при подстановке значения «0» вместо аргумента системы логических функций, имеющего вес , из числовой последовательности (2.2) мы получаем новую числовую последовательность, которая строится следующим образом: выписываются первые элементов исходной последовательности, вторые элементов пропускаются, затем выписываются следующие элементов и снова элементов пропускаются. И так продолжается до тех пор, пока мы не дойдём до конца исходной последовательности.

Пусть, например, мы имеем следующую числовую последовательность (2.5):

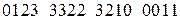. (2.5)

Подставив значение «0» вместо аргумента с весом 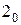, мы получим:

.

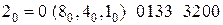Запись 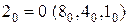означает, что вместо переменной c весом 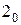подставлен ноль. Аргументами системы логических функций остались 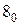, 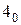и 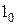, которые теперь имеют новые весовые коэффициенты 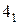, 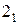и 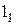соответственно.

2.2.2. Операция подстановки значения «1» вместо аргумента с весом .

Эта операция выполняется аналогично рассмотренной выше, с той лишь разницей, что процесс построения новой последовательности начинается с пропуска первых элементов исходной последовательности. Первые элементов исходной последовательности пропускаются, вторые – выписываются, третьи – снова пропускаются, четвёртые – выписываются. Это продолжается до тех пор, пока мы не дойдём до конца исходной последовательности.

Сделав подстановку 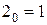в последовательность (2.5) мы получим:

.

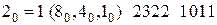2.2.3. Разложение числовой последовательности в матрицу по переменной с весом .

В результате выполнения этой операции над числовой последовательностью мы получаем числовую матрицу, имеющую две строки и 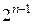столбцов. Первая строка матрицы получается подстановкой 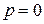в исходную последовательность, а вторая – подстановкой .

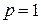Разложим, например, последовательность (2.5) по переменной с весом 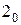. В результате получим матрицу 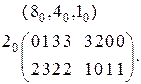(2.6):

(2.6)

Рядом c матрицей слева указывается вес переменной, по которой произведено разложение. Указанная переменная носит название выделенной переменной и изменяет своё значение с нуля на единицу по вертикали. Над матрицей указаны оставшиеся переменные, которые изменяют свои значения по горизонтали. Так как вертикальные и горизонтальные переменные взаимно дополняют друг друга до полного множества переменных, то горизонтальные переменные над матрицей можно не указывать.

2.2.4. Разложение числовой последовательности в матрицу по инверсному значению переменной с весом .

В результате выполнения этой операции над числовой последовательностью получается матрица с двумя строками и 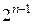столбцами. В первую строку записывается результат подстановки 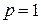, а во вторую – результат подстановки .

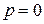Разложив последовательность (2.5), например, по инверсному значению переменной с весом 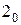, мы получим следующую матрицу:

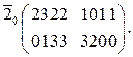
2.2.5. Развёртывание матрицы разложения по переменной с весом .

Эта операция является обратной по отношению к разложению числовой последовательности по переменной с весом . В результате из матрицы получается числовая последовательность, которая строится следующим образом: берутся первые элементов первой строки и к ним приписываются первые элементов второй строки, затем к ним приписываются вторые элементов первой строки и вторые элементов второй строки, и так до тех пор, пока мы не развернём всю матрицу.

В результате развёртывания матрицы (2.6) по переменной с весом 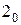, например, мы получим последовательность (2.5).

2.2.6. Исключение из последовательности фиктивной переменной с весом .

Утверждение 2.2. Переменная c весом называется фиктивной по отношению к некоторой числовой последовательности, если при разложении последней по этой переменной мы получаем матрицу с двумя одинаковыми строками.

Доказательство. Для элементов числовой последовательности, находящихся в одном столбце матрицы разложения все невыделенные переменные имеют одинаковые значения. При переходе от верхнего элемента столбца к нижнему изменяет своё значение только выделенная переменная . Таким образом, если при изменении значения переменной с весом , значение логической функции (или системы функций) не изменяется при любом фиксированном наборе значений остальных переменных, значит функция (или система) не зависит от переменной с весом (или говорят ещё, что зависит фиктивно). Если в результате разложения мы получаем матрицу с различными строками, то переменная с весом называется существенной.

Исключение фиктивной переменной, имеющей вес , производится разложением числовой последовательности по этой переменной и отбрасыванием одной из двух одинаковых строк полученной матрицы. Рядом с последовательностью мы должны указать в скобках оставшиеся существенные переменные.

Пусть, например, мы имеем числовую последовательность

.

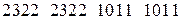Разложив её по переменной с весом 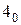, получим матрицу с двумя одинаковыми строками

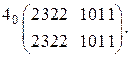
Исключив фиктивную переменную, получим следующую числовую последовательность:

.

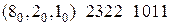В случаях, когда числовая последовательность представляет систему недоопределенных логических функций и имеет в своём составе звёздочки, для исключения фиктивной переменной строгого равенства строк матрицы разложения не требуется. Строки должны быть непротиворечивыми, то есть в одном столбце матрицы разложения не должно быть двух различных чисел. Может быть число и звёздочка или две звёздочки. Если в одном столбце имеется число и звёздочка, то в результирующей последовательности ставится на месте этого столбца число (т. е. последовательность доопределяется), а если две звёздочки, то ставится звёздочка.

Пусть, например, в результате разложения по переменной с весом 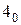мы получили следующую матрицу:

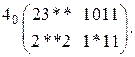
Тогда после исключения фиктивной переменной мы получим последовательность

.

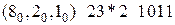2.2.7. Введение в последовательность фиктивной переменной с весом .

Эта операция является обратной исключению фиктивной переменной. Выполняется она следующим образом: заданная числовая последовательность повторяется дважды одна под другой и производится развёртывание полученной матрицы по весу соответствующей входной переменной.

Пусть мы имеем последовательность, определяющую функцию трёх переменных:

.

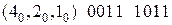Необходимо в последовательность ввести фиктивную переменную, которая должна иметь вес 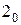. Для выполнения указанной операции построим матрицу

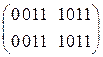
и развернём её по весу :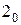

.

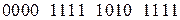Входная переменная 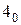теперь будет иметь вес 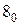, 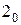– 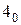, а переменная 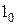своего значения не изменит.

2.2.8. Разложение числовой последовательности по нескольким входным переменным.

Пусть нам необходимо разложить некоторую числовую последовательность по двум входным переменным с весами и 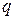, причём 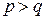. Для осуществления рассматриваемой операции необходимо вначале построить матрицу разложения последовательности по старшей входной переменной , а затем каждую из строк полученной матрицы разложить по младшей входной переменной 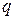. В результате получается матрица, имеющая четыре строки и 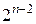столбцов.

В общем случае, если требуется разложить числовую последовательность по убывающим весам 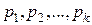, то первые 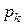элементов последовательности помещаются в первую строку результирующей матрицы, вторые 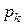элементов – во вторую, а затем – снова в первую, а после – во вторую. Так продолжается до тех пор, пока суммарное число, выбранных из последовательности элементов не сравняется с 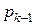. После этого начинают заполняться по тому же правилу третья и четвёртая строки матрица, пока мы снова не выберем 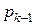элементов последовательности. Снова заполняются первая и вторая, а затем – третья и четвёртая строки матрицы. Как только общее число выбранных элементов последовательности сравняется с 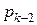, по тому же правилу заполняются пятая, шестая, седьмая и восьмая строки матрицы.

Пусть нам задана последовательность

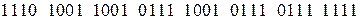
и её требуется разложить по весам 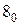, 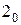и 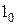. При построении матрицы разложения первый элемент последовательности помещается в первую строку матрицы, а второй – во вторую. Суммарное число выбранных элементов равняется следующему весу 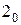и, поэтому, переходим к заполнению третьей и четвёртой строк. Третий элемент последовательности помещается в третью строку, а четвёртый – в четвёртую. Мы снова выбрали два элемента, а общее их число пока меньше восьми. Поэтому снова возвращаемся к заполнению первой и второй (но уже в новых столбцах матрицы), а затем – третьей и четвёртой строк. Девятый элемент последовательности помещается в пятую строку, десятый – в шестую, одиннадцатый – в седьмую, двенадцатый – в восьмую. Так как мы ещё не выбрали пока новые восемь элементов, то тринадцатый элемент последовательности помещается во второй столбец пятой строки. И так далее по шестнадцатый элемент последовательности включительно. Семнадцатый элемент снова записывается в первую строку и всё повторяется снова. В результате получается следующая матрица:

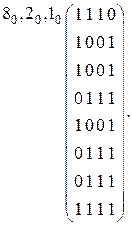
Далее рассмотрим операции второй группы, которые выполняются над самими функциями системы.

2.2.9. Разделение числовой последовательности на старшую и младшую составляющие.

Это разделение производится по весам разрядов двоичных эквивалентов чисел последовательности. Двоичный эквивалент каждого числа исходной числовой последовательности разделяется на две части относительно веса некоторого разряда. В младшую часть попадают те разряды, вес которых меньше, чем , а в старшую все остальные. Вес является целой степенью двойки. Пусть 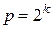. Тогда любое число 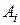в последовательности (2.2) можно представить в следующем виде:

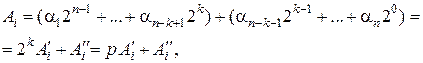(2.7)

где 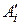– старшая составляющая числ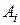а , а 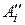– младшая. Для того, чтобы число 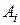разделить на старшую и младшую составляющие относительно некоторого веса , нужно его разделить на . Целая часть от деления даст старшую часть, а остаток – младшую. Если каждый элемент последовательности (2.2) мы разделим на старшую и младшую составляющие, то получим две последовательности – старшую и младшую.

Пусть, например, числовую последовательность

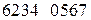(2.8)

требуется разделить на старшую и младшую составляющие относительно веса 4. Каждое число заданной числовой последовательности разделим на 4 и получим следующие две последовательности целых частей и остатков:

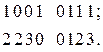
2.2.10. Объединение числовых последовательностей.

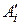Объединяться могут только последовательности одинаковой длины, определяющие системы логических функций от одних и тех же аргументов. Одна из последовательностей выбирается в качестве старшей, а другая – в качестве младшей. Определяется самый старший вес младшей последовательности и удваивается. С помощью найденного, таким образом веса для каждой пары и 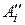по формуле (2.7) находится число 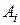, которое является элементом объединённой последовательности.

Пользуясь операцией разделения можно из числовой последовательности системы логических функций выделить двоичную последовательность любой из составляющих эту систему логических функций. Совместно с операцией объединения операция разделения позволяет произвольным образом изменять веса двоичных последовательностей в общей числовой последовательности.

2.2.11. Логические операции над числовыми последовательностями.

К числовым последовательностям можно применять все известные логические операции. Одноместная операция «НЕ» над числовой последовательностью означает поразрядную инверсию двоичного представления каждого числа последовательности.

Найдём, например, инверсию последовательности (2.8). Число 6 в двоичной системе записывается как 110. Взяв, поразрядную инверсию этого кода, получим 001, то есть число 1. Число 2 записывается как 010, которое после поразрядной инверсии запишется как 101, то есть 5. И так далее. В результате получим следующую числовую последовательность:

.

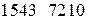Двухместные логические операции могут выполняться только над последовательностями одинаковой длины и определяющими системы логических функций от одних и тех же аргументов. Операция выполняется над каждой парой чисел с одним и тем же индексом .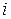

В качестве примера выполним операцию «И» над последовательностям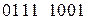и

и

.

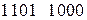В результате получим последовательность

.
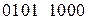