Методы решения систем уравнений установившегося режима
2.1 Классификация методов решения уравнений установившегося режима электрической системы
Системы уравнений установившегося режима – это системы нелинейных алгебраических (или тригонометрических, трансцендентных) уравнений (СНАУ) или (СТУ). Классификация методов их решения схематически выглядит так.
| Методы решения систем нелинейных алгебраических или тригонометрических уравнений установившегося режима | |||||
Преобразование нелинейных уравнений в линейные – внешняя итерация. На каждом шаге внешней итерации решается система линейных алгебраических уравнений 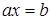 относительно неизвестных х. Методы решения систем линейных алгебраических уравнений относительно неизвестных х. Методы решения систем линейных алгебраических уравнений | ||||
| Численные методы решения систем нелинейных алгебраических уравнений. | ||
| Метод последовательного упорядоченного исключения неизвестных (метод Гаусса) |
| Итерационные (приближённые, численные) |



| Точные (прямые) |
| Метод ускоренной итерации (Гаусса-Зейделя) | Метод Ньютона. На каждом шаге итераций решается система линейных алгебраических уравнений относительно поправок к неизвестным Δх |

| Метод простой итерации |
| Метод ускоренной итерации (Гаусса-Зейделя) |


| Метод, основанный на обращении матрицы узловых проводимостей. Yу-1=zy—это матрица узловых сопротивлений, поэтому этот метод называют методом узловых сопротивлений |






| Метод LU разложения |
Полученные узловые и контурные уравнения представляют собой матричные математические модели электрической системы. Матричные математические модели очень часто используются в исследованиях электрических систем для компактной записи систем алгебраических уравнений, формирования с помощью ПК таких уравнений, усовершенствования существующих и разработки новых методов решения.
Матричные методы расчёта, т.е. методы в которых выполняются операции с матрицами, распространены значительно меньше. В расчётах сложных электрических систем матричные методы, предусматривающие использование стандартных подпрограмм, неэффективны, поскольку требуют значительных вычислительных ресурсов ЭВМ.
Факторами, определяющими эффективность процесса решения инженерных задач на ЭВМ, являются:
1 Надежность вычислительного процесса – построение алгоритма, исключающего появление чрезмерно больших погрешностей при решении задач прямыми методами и обеспечивающих быструю сходимости при использовании итерационных методов.
2 Экономное использование памяти ЭВМ и сокращение времени вычислений за счёт рационального (компактного) представления исходных данных о системе с учётом её структурных свойств.
3 Гибкость алгоритма и программы, т.е. возможность различной степени детализации электрической системы и лёгкость учёта изменений расчетной схемы системы, в зависимости то цели исследования.
2.2 Методы решения систем линейных алгебраическихуравнений
Как показано выше, уравнения установившегося режима электрической системы нелинейные. Однако мы их можем линеаризовать, применив метод внешней итерации, т.е. задавшись приближенными значениями напряжений в узлах, определить задающие токи, затем, найдя напряжения, уточнить их.
Получающиеся линейные уравнения (это могут быть узловые уравнения или контурные уравнения, рассмотренные выше) могут решаться методами, которые делятся на две группы: точные (прямые) и итерационные или приближенные.
2.2.1 Точные методы решения систем линейных алгебраическихуравненийустановившихсярежимов
Точными методами называются такие, которые в предложении, что все вычисления ведутся точно (без округлений), позволяют получить точные значения неизвестны в результате конечного числа операций. К ним относятся:
2.2.1.1 Метод, основанный на обращении матрицы коэффициентов (узловых проводимостей)
Методы, основаны на обращении матриц коэффициентов:
1.1 классический;
1.2 обращение методом разбиения на клетки;
1.3 обращение методом окаймления;
1.4 обращение методом Гаусса.
Во всех этих методах, по сравнению с классическим, обращение упрощается, т.к. приходиться обращать матрицу меньшего порядка. В методе окаймления операция обращения сводится к вычислению обратного числа.
Использование матрицы узловых сопротивлений Zy=Y-1y целесообразно в случае, когда необходимо многократно решать системы уравнений с одинаковыми коэффициентами при неизвестных (при неизменной схеме) и различных значений свободных членов (правых частей) при разных значениях нагрузок. Наиболее часто это встречается в многоразовых расчетах токов КЗ, а также при многократных расчетах установившихся режимов при их оптимизации, в расчётах электромеханических переходных процессов и др. Разработаны эффективные методы коррекции матрицы Zy при незначительных изменениях расчётной схемы.
2.2.1.2 Метод последовательного упорядоченного исключениянеизвестных(методГаусса)
Две системы уравнений называются эквивалентными, если обе системы имеют одно и то же решение или, другими словами, если решение одной системы автоматически является решением другой системы и наоборот.
Рассматриваемый метод основан на построении эквивалентной системы уравнений, решение которой легко найти непосредственно. Решение этой системы одновременно является решением исходной системы.
При построении эквивалентных систем уравнений используют элементарные операции над уравнениями:
1. умножение любого уравнения системы на положительное или отрицательное число;
2. сложение любого уравнения с любым другим уравнением схемы, умноженным на константу (положительную или отрицательную).
