Обращение матрицы коэффициентов системы уравнений установившегося режима

Ранее рассмотренные методы решения СЛАУ позволяют определить ре-шение системы, записанной в виде

Ax=B => 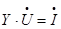. (1)

Часто требуется многократное решение систем уравнений установив-шегося режима при неизменной схеме электрической сети и её параметров и различных наборах заданных значений токов в узлах. Это означает, что мат-рица проводимостей Y остается неизменной, а изменяющимися являются зна-чения вектора свободных членов I. В этом случае решение системы уравне-ний (1) целесообразно искать в виде

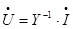, (2)

то есть матрица проводимостей обращается один раз, а решение системы уравнений при изменяющихся значениях элементов вектора І сводится к многократному умножению матрицы Y^-1 на новый вектор I.

Обращение матрицы проводимостей требует большого объема вычисле-ний. Существует различные методы обращения матрицы.

Обращение матриц методом упорядоченного исключения неизвестных

В соответствии с определением обратной матрицы - прямая матрица А, будучи умноженной на обратную матрицу А^-1, дает единичную матрицу Е, можно записать:

.

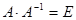Если исходная матрица : ,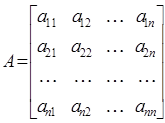

искомая обратная матрица: ,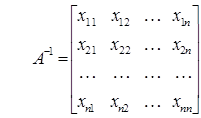

тогда их произведение:

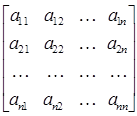
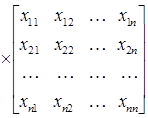
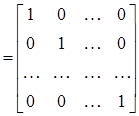
Перемножая строки матрицы А поочередно на столбцы матрицы А^-1, получаем n систем линейных уравнений, в каждой из которых в правой части будут элементы соответствующего столбца единичной матрицы, а неизвест-ными – элементы соответствующего столбца обратной матрицы.

При умножении первой строки матрицы А на первый столбец матрицы А^-1, получаем в правой части первый элемент 1-го столбца единичной матри-цы. Он равен 1. Умножив вторую строку матрицы А на 1-й столбец матрицы А^-1 получаем 2 –й элемент 1 – го столбца единичной матрицы (он равен 0) и т.д. Перемножив все n строк исходной матрицы А на 1- й столбец матрицы А^-1, получаем систему уравнений, в правой части которой – элементы 1–го столбца единичной матрицы, неизвестные – элементы 1–го столбца обрат-ной матрицы x_і1 ( і = 1, ... n ):

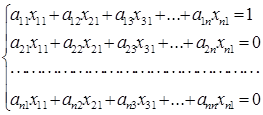
Решив эту систему уравнений, определим элементы первого столбца ис-комой обратной матрицы.

Вторую систему уравнений получим умножением матрицы А на второй столбец обратной матрицы. В полученной системе уравнений: в правой части – элементы 2–го столбца единичной матрицы, неизвестные – 2–й стол-бец обратной матрицы x_i2 ( I = 1, … ,n):

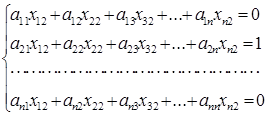
Решив эту систему уравнений, найдем элементы второго столбца обрат-ной матрицы.

Перемножаем т.о. матрицу А на остальные столбцы матрицы А^-1. При умножении на последний столбец , получаем систему уравнений и решаем её:

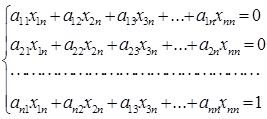
В результате получили n независимых систем линейных уравнений с n неизвестными (элементы столбцов искомой обратной матрицы). Каждая система состоит из n уравнений. Решая их любым из известных методов, определим элементы обратной матрицы.

Метод прост алгоритмически, но требует большого объёма вычислений.