Алгебраизация обыкновенных дифференциальных уравнений

Требуется найти решение системы обыкновенных дифференциальных уравнений (ОДУ):

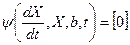
При известных начальных условиях t = t₀, Х₀

Алгебраизация заключается в сведении системы ОДУ к системе конечных (алгебраических) уравнений, решаемых одним из изученных методов.

В случае линейных ОДУ их алгебраизация производится с использованием символьного или операторного методов.

В общем случае как линейных, так и нелинейных ОДУ алгебраизация ОДУ заключается в аппроксимации производных некоторыми выражениями, например отношениями конечных разностей.

Вид аппроксимирующего выражения влияет на точность, устойчивость и скорость вычислений. Методы интегрирования ОДУ различают по виду таких выражений.

Очевидно, что аппроксимация производных некоторыми конечными выражениями, выполненная при некотором значении времени t_k справедлива лишь в окрестности этой точки, ограниченной величиной шага интегрирования h.

Для нахождения зависимости на интервале от 0 до T_k необходимо сделать

Ш =(t_k – t₀) /h,

где Ш – число шагов интегрирования.

Численное решение является приближенным. Оно имеет 2 группы погрешностей:

1) Методические, связанные с аппроксимацией производных (они зависят от метода интегрирования).

2) Округления – обусловленные конечной точностью представления чисел в ЭВМ.

Различают также локальныепогрешности, допущенные на одном шаге интегрирования и накопленные, на определенном интервале за много шагов.

Методы интегрирования делятся на явные и неявные.

В явных методах решение определяется явным способом:

X_k+1 = f(X_k; X_k-1; t_k+1).

В неявныхметодах, находят решение системы уравнений:

F(X_k+1; X_k; …. t_k+1)= 0.

Различают по характеру изменения накопленной погрешности на устойчивые и неустойчивые.

В устойчивом - погрешность растёт монотонно с увеличением шага.

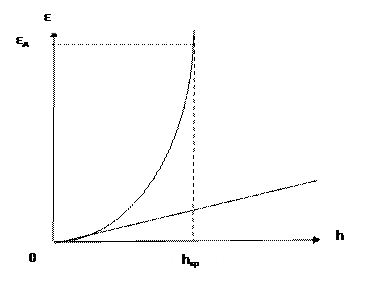
В неустойчивом – начиная с некоторого критического значения шага интегрирования происходит резкий (катастрофический) рост погрешности.

Различают методы различных порядков по величине накопленной погрешности.

ε ~ ψ(t)hⁿ, где n – порядокметода.

Явные методы

Применяют, когда производная выражена явно: 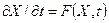, т.е. в нормальной форме Коши.

Известны начальные условия:

t = t₀; X = X₀

Разложим в ряд Тейлора интегральную кривую x_j(t) в окрестности точки t_k:

x_j (t_k+1) = x_j(t_k) + dx_j(t_k)/dt *h + (1/2!) d²x(t_k)/dt² * h²+…

h = t_k+1 -t_k

dx_j(t_k)/dt = f_j( x_k, t_k)

d²x_j(t_k)/dt² =[ f_j( x_k, t_k) - f_j( x_k-1, t_k-1) ]/h

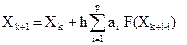- общая формула всех явных методов.

Метод Эйлера

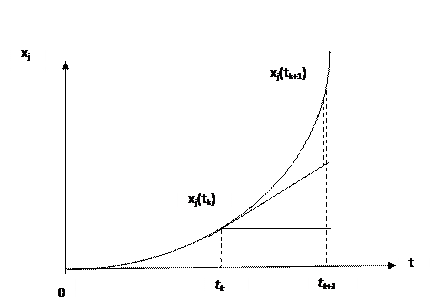
Это - метод первого порядка. Расчет ведется по формуле

X_k+1= X_k+ h F(X_k,t_k).

Она получается из общей формулы при p = 1.

Методическая погрешность метода оценивается старшим отбрасываемым членом.

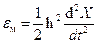
На некотором интервале t₀,t суммарная накопленная погрешность ε ,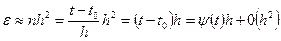

где 0(h²)- величина, ограниченная по сравнению с h².